Area → Volume
Recall from single-variable calculus that the definite integral of a single-variable function $f(x)$ over the interval $a \le x \le b$ gives the exact area under the curve between those limits. Here's the diagram. We developed this idea by first considering the Riemann sum of rectangles under the curve, then taking their width to be infinitely thin while summing an infinite number of them.

We can extend this idea to functions of two variables with three-dimensional graphs, like $f(x, y)$.
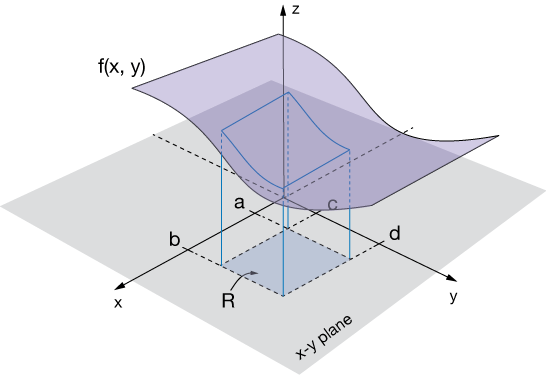
Here is the analog of that 2D graph in three dimensions. Our function $f(x, y)$ is some kind of surface (purple), and instead of a linear interval $[a, b]$, we define a region, $R$, in the $xy$-plane over which we'd like to find the volume under $f(x,y)$ — the red region.

We do that by first integrating shapes along one axis ($x$ or $y$), then along the other. The order won't turn out to matter.
Now that region $R$ can take on many forms. It can be rectilinear or curved, and much of our job in this section will be to define the limits of integration.
Review of integrals in $\mathbb R^2$
Here's a refresher of how we derive the integral form for the area under a curve. The graph below shows a function $f(x)$, which we'll assume has a value greater than zero over the interval of interest, $[a, \; b]$. We divide the interval up into boxes of width $\Delta x$.
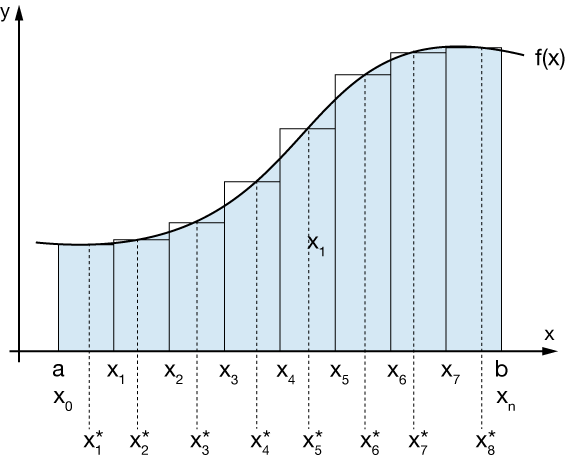
The height of each is determined by a point ($x_i^*$) — guaranteed to exist by the mean value theorem — at which the curve has the same slope (derivative) as the average slope across that box.
If we reduce the width of the boxes ($\Delta x$), the height is always $f(x_i^*)$, where the point $x_i^*$ may move around a bit, but will always exist to represent the height of the bar, no matter how much we shrink its width.
The approximate area under the curve is
$$\sum_{i=1}^n f(x_i^*) \Delta x,$$
where $n$ is the number of boxes — which is inversely proportional to their width.
Now if we increase the number of boxes to infinity, we get our definite integral:
$$A = \int_a^b f(x) \, dx = \lim_{n \to \infty} \sum_{i=1}^n f(x_i^*) \Delta x$$
Now we'll extend this idea to the $\mathbb R^3$ case.
Extension to $\mathbb R^3$
The extension to $\mathbb R^3$ is pretty straightforward. Consider the surface $f(x,y)$ shown below (purple), with a rectangular region on the $xy$ plane below (blue). For now we'll assume that $f(x,y) \gt 0$. The region $R$ is a rectangle with sides of length $b-a$ and $d-c$.
Now let's look at the region $R$ in the $xy$ plane. We can divide it up into rectangles of area $\Delta x \Delta y$, which form the bases of rectangular prisms which will fill the space under our function and over $R$ — in the same way as we used 2D boxes in the $\mathbb R^2$ case.
Inside each box is a point $(x_i^*, \; y_j^*)$ that has the same slope as the average slope of a plane spanning the top of the 3D box and tangent to the function at a point that has that same slope. This point is guaranteed to exist (according to the mean value theorem) no matter how small we make each rectangle — and we'll want to make them infintely small.
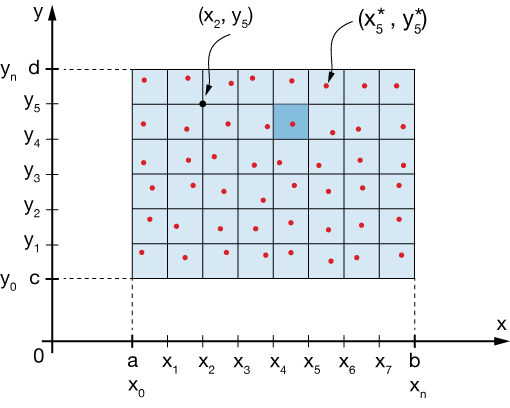
An approximation of the volume over $R$ and under $f(x,y)$ is just the sum of volumes of boxes of width $\Delta x \Delta y$ with height $(x_i^*, \; y_j^*)$:
$$V \approx \sum_{i=1}^m \sum_{j=1}^n f(x_i^*, \; y_j^*) \Delta x \Delta y$$
If you know a little bit of computer coding and nested loops, the double sum means to increment the outer sum (say $i=1$, then loop through the whole range of $j$, then increment $i$, do all of the $j$ sum again, and so on. Then the exact volume is found by taking the limit as $m$ and $n$ go to infinity, which means that $\Delta x$ and $\Delta y \; \rightarrow 0$:
$$ \begin{align} \lim_{m, n \to \infty} &\sum_{i=1}^m \sum_{j=1}^n f(x_i^*, \; y_j^*) \Delta x \Delta y \\[5pt] &= \int_a^b \, dx \int_c^d dy \, f(x,y) \end{align}$$
About the notation
When doing single-variable integrals we usually write
$$\int_a^b \, f(x) \, dx$$
but we can also write
$$\int_a^b \, dx \, f(x)$$
without any loss of meaning. This second form can be helpful when writing definite double integrals because it helps us to keep the work organized. Consider that
$$\int_a^b dx \int _c^d dy f(x) = \int_a^b dx \left( \int_c^d dy \, f(x,y) \right)$$
If it's more comfortable, however, you can still write this double integral like this:
$$\int_a^b \int_c^d \, f(x) \, dy \, dx = \int_a^b \left(\int_c^d \, f(x) dy \right) dx$$
A simple example
The region, $R$, over which we integrate can have a few different forms. It can be
- rectilinear (rectangular or square);
- the area enclosed by two or more intersecting curves; or
- the area inside of a closed curve like a circle or an ellipse or some other closed figure made of curves and lines.
Let's start with a simple example, the plane with equation $3y - z = 0$. This plane contains the $x$ axis and extends infinitely in the $\pm x$ directions as shown in the second graph. We'll try to find the volume under this plane between $-4 \le x \le 4$ and $0 \le y \le 4$.
If we forget about the $x$ dimension, we can easily integrate to find the area under the curve $z = 3y$, shown below.

Looking down the $x$-axis, the function to integrate is $z = 3y$, and the area under it from $y = 0$ to $y = 4$ is
$$ \begin{align} A = \int_0^4 3y \, dy &= \frac{3y^2}{2} \bigg|_0^4 \\[5pt] &= \frac{3}{2}(16 - 0) = 24 \text{ units}^2 \end{align}$$
We can double check this integral by noting that the shaded region is a right triangle with area
$$A = \frac{1}{2} bh = \frac{1}{2} (4)(12) = 24 \text{ units}^2$$
Now if we look at the 3D graph of the plane $3y - z = 0$, we can imagine a large number (which we'll extend to an infinite number) of such triangles stacked along the $x$-axis between $x = -4$ and $x = 4$. We can add these up by integrating between $x=-4$ and $x=4$:
$$V = \int_{-4}^4 24 \, dx = 24x \bigg|_{-4}^4 = 24(8) = 192 \text{ units}^3$$

We can combine these integration operations into a double integral like this:
$$ \begin{align} \int_{-4}^4 &\left[ \int_0^4 3y - z \; dy \right] \, dz \\[5pt] &= \int_{-4}^4 \frac{3}{2}y^2 \, \bigg|_0^4 \, dz = \int_{-4}^{4} \, 24 \, dz \\[5pt] &= 24 z \bigg|_{-4}^4 = 24(8) = 192 \text{ units}^3 \end{align}$$
Notice that we've written an inner and an outer integral here, integrals with respect to variables $y$ and $z$, respectively. It turns out that the order of integration (after all it's just addition) doesn't matter. We also usually omit the square brackets we used above and just nest these integrals like this:
$$\int_{-4}^4 dz \int_0^4 dy \, (3y - z) $$
The understanding is that we do the inner $(dy)$ integral first, complete with evaluation of the limits, then we do the outer $(dz)$ integral.
Pro tip:
The order of integration in multiple integrals doesn't matter, but sometimes one order might make the overall integral easier to do than another.
Example 1
Find the volume under the paraboloid $f(x,y) = 4 - x^2 - y^2$ and over the rectangular area defined by $x \in [0, 1]$ and $y \in [-1, 1]$.
Here's a picture of what we're trying to do. we'd like to find the volume inside the rectangular area outlined under the downward-opening paraboloid. The second graph is a top view of the same situation.

The integral setup is fairly easy:
$$V = \int_0^1 dx \int_{-1}^1 dy \, (4 - x^2 - y^2)$$
In this version, we'll do the $dy$ integral first, including evaluation of its limits, then the $dx$ integral. We'll see later that the order doesn't matter. Here's the integral:
$$ \require{cancel} \begin{align} V &= \int_0^1 dx \int_{-1}^1 dy \, (4 - x^2 - y^2) \\[5pt] &= \int_0^1 dx \left[ 4y - x^2y - \frac{y^3}{3} \right]_{-1}^1 \\[5pt] &= \int_0^1 dx \left[ 4 - x^2 - \frac{1}{3} - (-4 + x^2 + \frac{1}{3})\right] \\[5pt] &= \int_0^1 dx \left[ 8 - \frac{2}{3} - x^2 \right] \\[5pt] &= \int_0^1 dx \left[ \frac{22}{3} - 2x^2 \right] \\[5pt] &= \left[ \frac{22}{3}x - \frac{2}{3}x^3 \right]_0^1 \\[5pt] &= \frac{22}{3} - \frac{2}{3} \\[5pt] &= \frac{20}{3} \text{ units}^3 \end{align}$$

We should just check to see that integrating in the other order doesn't make a difference:
$$ \require{cancel} \begin{align} V &= \int_{-1}^1 dy \int_0^1 dx \, (4 - x^2 - y^2) \\[5pt] &= \int_{-1}^1 dy \left[ 4x - \frac{x^3}{3} - y^2x \right]_0^1 \\[5pt] &= \int_{-1}^1 dy \left[ 4 - \frac{1}{3} - y^2\right] \\[5pt] &= \int_{-1}^1 dy \left[ \frac{11}{3} - y^2 \right] \\[5pt] &= \left[ \frac{11}{3}y - \frac{y^3}{3} \right]_{-1}^1 \\[5pt] &= \left[ \frac{11}{3} - \frac{1}{3} + \frac{11}{3} - \frac{1}{3} \right]_0^1 \\[5pt] &= \frac{22}{3} - \frac{2}{3} \\[5pt] &= \frac{20}{3} \text{ units}^3 \end{align}$$
So indeed they are the same.
A property of double integrals
$$\int_a^b dx \int_c^d dy \, f(x,y) = \int_c^d dy \int_a^b dx \, f(x,y)$$
2D integrals
We can use double integration to find areas between curves on a 2D plane, too. Here's an example. Let's find the area between the curves $y = 3-x^2$ and $y = x$. Here's the braph of those functions with the area highlighted.

To define the area we should find the intersections by equating the two functions:
$$ \begin{align} 3 - x^2 &= x \\[5pt] x^2 + x - 3 &= 0 \tag{1} \\[5pt] x^2 + x + \bigg( \frac{1}{2} \bigg)^2 &= 3 + \frac{1}{4} \\[5pt] \bigg( x + \frac{1}{2} \bigg)^2 &= \frac{13}{4} \\[5pt] x &= \frac{-1 \pm \sqrt{13}}{2} \end{align}$$
Here we've completed the square to get the solutions to the quadratic equation (1). Now in the figure an area element, $\Delta A$ is shown. We'll add up an infinite number of such area elements, $dA = dy \, dx$, to find our total area. For brevity, we'll express our intersections as decimal numbers, $x = -2.303, \, 1.303$. The integral is:
$$\int_{-2.303}^{1.303} \int_x^{3-x^2} dy \, dx$$
We integrate along the $x$-coordinate between the intersections and along the $y$-coordinate between the two functions. Now it's an easy solution:
$$ \begin{align} &\int_{-2.303}^{1.303} \int_x^{3-x^2} dy \; dx \\[5pt] &= \int_{-2.303}^{1.303} \, (3 - x^2 - x) \, dx \tag{2} \\[5pt] &= 3x -\frac{x^3}{3} - \frac{x^2}{2} \bigg|_{-2.303}^{1.303} \\[5pt] &= 3(1.303) - \frac{1.303^3}{3} - \frac{1.303^2}{2} \\[5pt] &\phantom{000000} - 3(-2.303) + \frac{(-2.303)^3}{3} + \frac{(-2.303)^2}{2} \\[5pt] &= 8.09 \text{ units}^2 \end{align}$$
Notice that the integral in (2) is just the integral we would construct using 1D calculus to find this area. It's the integral of the top function minus the bottom function, between the intersections.
Example 2
Now let's do an example of 2D integration over a non-rectangular area. Calculate the volume under the plane $f(x,y) = 2x + y$ above the region bounded by the parabolas $y = 2x^2$ and $y = x^2 + 1$.
First, let's look at that region in the $xy$-plane.

To find the volume over this region and under $f(x,y) = 2x + y$, we'll need to take a little more care in setting up our limits of integration. If we choose to integrate in the $y$-direction first, the limits as we move along the $x$-axis are $2x^2 \le y \le x^2+1$. That establishes the shape of our 2D region, and all that remains is to integrate over the integral $-1 \le x \le 1$ in the $x$-dimension. Our double integral will look like this:
$$\int_{-1}^1 dx \int_{2x^2}^{x^2+1} (2x + y)$$
Here's the solution
$$ \begin{align} V &= \int_{-1}^1 dx \int_{2x^2}^{x^2+1} dy \, (2x + y) \\[5pt] &= \int_{-1}^1 dx \left[ 2xy + \frac{y^2}{2} \right]_{2x^2}^{x^2+1} \\[5pt] &= \int_{-1}^1 dx \left[ 2x(x^2+1) + \frac{(x^2+1)^2}{2} - 4x^3 - \frac{4x^4}{2} \right] \\[5pt] &= \int_{-1}^1 dx \left[2x^3 + 2x + \frac{1}{2}x^4 + \frac{1}{2}(2x^2) + \frac{1}{2} - 4x^3 - 2x^4 \right] \\[5pt] &= \int_{-1}^1 dx \left[ -\frac{3}{2} x^4 -2x^3 + x^2 + 2x + \frac{1}{2} \right] \\[5pt] &= \left[ -\frac{3}{10} x^5 - \frac{1}{2}x^4 + \frac{x^3}{3} + x^2 + \frac{1}{2}x \right]_{-1}^1 \\[5pt] &= \frac{-3}{10} - \cancel{\frac{1}{2}} + \frac{1}{3} + \cancel{1} + \frac{1}{2} - \frac{3}{10} + \cancel{\frac{1}{2}} + \frac{1}{3} - \cancel{1} + \frac{1}{2} \\[5pt] &= \frac{16}{15} \text{ units}^3 \end{align}$$
Example 3
Now let's do a more complicated example. Calculate the volume under the curve $f(x,y) = 9 - x^2 - y^2$ and above the $x-y$ plane.
Here's a graph of the function. We're trying to find the volume between the top at $z = 9$ and the $xy$-plane.

We can take advantage of the symmetry of the function and just solve for ¼ of it, just the part in the first octant of a 3D graph:

We'll set up our double integral to first integrate along the $y$-axis, then along the $x$-axis. The limits of integration will be $0$ to $y = \sqrt{9-x^2}$ along the $y$ direction and $0$ to $3$ along the $x$. Recall that the base of the figure is the circle $x^2 + y^2 = 9$.
Our integral is
$$ \require{cancel} \begin{align} V &= 4 \int_0^3 \int_0^{\sqrt{9-x^2}} 9 - x^2 - y^2 \, dy \, dx \\[5pt] &= 4 \int_0^3 \left[ 9y -x^2y - \frac{y^3}{3} \right]_0^{\sqrt{9-x^2}} \, dx \\[5pt] &= 4 \int_0^3 \left[ (9 -x^2)y - \frac{y^3}{3} \right]_0^{\sqrt{9-x^2}} \, dx\\[5pt] &= 4 \int_0^3 \left[ (9-x^2)^{\frac{3}{2}} - \frac{1}{3} (9-x^2)^{\frac{3}{2}} \right] \, dx \\[5pt] &= \frac{8}{3} \int_0^3 (9-x^2)^{\frac{3}{2}} \, dx \tag{1} \end{align}$$
This integral can be done using trig substitution:
$$ \begin{align} \text{Let } \; x &= 3 \, \text{sin}(t)\\[5pt] \text{Then } \; x^2 &= 9 \, \text{sin}^2(t) \\[5pt] \text{and } \; 9 - x^2 &= 9 - 9 \, \text{sin}^2(t) \\[5pt] &= 9(1-\text{sin}^2(t)) \\[5pt] &= 9 \, \text{cos}^2(t) \\[5pt] \text{Then } \; (9 - x^2)^{\frac{3}{2}} &= 9^{\frac{3}{2}} \left( \text{cos}^{\cancel{2}}(t) \right)^{\frac{3}{\cancel{2}}} \\[5pt] &= 27 \, \text{cos}^3 (t) \\[5pt] \text{And finally we need } dx &= 3 \, \text{cos}(t) \, dt \end{align}$$
Our original integral (see (1) above) then converts to
$$ \begin{align} \frac{8}{\cancel{3}} &\int_0^{\frac{\pi}{2}} \, 27 \, \text{cos}^3(t) \, \cancel{3} \, \text{cos}(t) \, dt \\[5pt] &= 216 \int_0^{\frac{\pi}{2}} \left( \frac{1 + \text{cos}(2t)}{2} \right)^2 \end{align}$$
where in the second line we've used the power reduction formula for $\text{cos}^2(\theta)$.
Now we can expand the integrand:
$$ \begin{align} \frac{216}{4} &\int_0^{\frac{\pi}{2}} 1 + 2 \text{cos} (2t) + \text{cos}^2(2t) \, dt \\[5pt] &= 54 \int_0^{\frac{\pi}{2}} 1 + 2 \text{cos}(2t) + \frac{1}{2} + \frac{1+\text{cos}(4t)}{2} \, dt \\[5pt] &= 54 \int_0^{\frac{\pi}{2}} 1 \, dt + 108 \int_0^{\frac{\pi}{2}} \text{cos}(2t) \, dt \\[5pt] &\phantom{0000} + 27 \int_0^{\frac{\pi}{2}} dt + 27 \int_0^{\frac{\pi}{2}} \text{cos}(4t) \, dt \\[5pt] &= 54 \bigg|_0^{\frac{\pi}{2}} + \cancel{54 \, \text{sin}(2t) \bigg|_0^{\frac{\pi}{2}}} + 27t \bigg|_0^{{\pi}{2}} + \cancel{\frac{27}{4} \text{sin}(4t) \bigg|_0^{\frac{\pi}{2}}} \\[5pt] &= 54 \frac{\pi}{2} + 27 \frac{\pi}{2} \\[5pt] &= \frac{81 \pi}{2} = 127.23 \text{ units}^3 \end{align}$$
Check with the disk method
We can check this volume by doing a simpler integral using the disk method. The figure shows how we add disks along the $z$-axis from $z=0$ to $z=9$.

Here's the integral:
$$ \begin{align} V &= \int_0^9 \pi (\sqrt{9-z})^2 \, dz \\[5pt] &= \pi \int_0^9 (9 - z) \, dz \\[5pt] &= \pi \left[ 9z - \frac{z^2}{2} \right]_0^9 \\[5pt] &= \pi \left[9(9) - \frac{9^2}{2} - 0 + 0 \right] \\[5pt] &= \pi \left[ 81 - \frac{81}{2} \right] \\[5pt] &= \frac{81 \pi}{2} \; \color{green}{\checkmark} \end{align}$$
Now, you might be asking, if this volume was so simple to find with the disk method and single integration, why did we do it with double integrals? Fair point. But we won't always have such nice symmetry when finding volumes and solving other kinds of multidimensional integration problems, so it was worth going through. Plus, it's a nice reminder of some of our integration techniques.
Practice problems
Solve the following double integrals:
-
$\int_0^1 dx \, \int_1^2 dy \, \left( \frac{x \, e^x}{y} \right)$
Solution
$$ \begin{align} \int_0^1 dx \, &\int_1^2 dy \, \left( \frac{x \, e^x}{y} \right) \\[5pt] &= \int_0^1 dx \left[ x \, e^x \, ln(y) \right]_1^2 \\[5pt] &= \int_0^1 dx \left[ x \, e^x (ln(2) - ln(0)) \right] \\[5pt] &= ln(2) \int_0^1 x \, e^x \, dx \end{align}$$
We can solve this integral by parts:
$$ \begin{align} \text{Let } u &= x \phantom{000} dv = e^x \, dx \\[5pt] \text{then } \; du &= dx \phantom{0} \text{ and } \phantom{0} v = e^x \end{align}$$
$$ \begin{align} \int x \, e^x \, dx &= x \, e^x - \int e^x \, dx \\[5pt] &= e^x (x - 1) \end{align}$$
Plugging this into our double integral, we get
$$ \begin{align} &= ln(2)\, e^x (x-1) \bigg|_0^1 \\[5pt] &= ln(2) \left[ e(0) -1(-1) \right] = ln(2) \end{align}$$
-
$\int_0^1 dx \int_2^{2x} dy \, (y-x)$
Solution
$$ \begin{align} \int_0^1 dx &\int_2^{2x} dy \, (y-x) \\[5pt] &= \int_0^1 dx \left[ \frac{y^2}{2} - xy \right]_2^{2x} \\[5pt] &= \int_0^1 dx [2x - 2] \end{align}$$
$$ \begin{align} &= \left[ x^2 - 2x \right]_0^1 \\[5pt] &= 1-2-0+0 \\[5pt] &= -1 \end{align}$$
-
$\int_0^1 dx \int_0^1 dy \sqrt{x+y}$
Solution
$$\int_0^1 dx \int_0^1 dy \sqrt{x+y}$$
$$ \begin{align} \text{Let } u &= x+y \; \text{ , then } \; du = dy \\[5pt] y &= 0 \; \rightarrow \; u = x, \\[5pt] y &= 1 \; \rightarrow \; u = x+1 \end{align}$$
Now note the change of variables in the first integral.
$$ \begin{align} \int_0^1 dx &\int_x^{x+1} u^{\frac{1}{2}} du \\[5pt] &= \frac{2}{3} \int_0^1 dx \, (x+1)^{\frac{3}{2}} - x^{\frac{3}{2}} \\[5pt] &= \frac{2}{3} \left[ \frac{2}{5}(x+1)^{\frac{5}{2}} - \frac{2}{5} x^{\frac{5}{2}} \right]_0^1 \\[5pt] &= \frac{4}{15} \left[ 2^{\frac{5}{2}} - 1^{\frac{5}{2}} -0+0 \right] \\[5pt] &= \frac{4}{15} (32 - 1) = \frac{124}{15} \end{align}$$
-
Calculate the double integral over region $R$, $\iint_R \frac{y}{x^5+1} \, dA$, where $R = \{(x,y)|0 \le x \le 1, 0 \le y \le x^2 \}$
Solution
First let's have a look at the region, $R$.

The integral setup is
$$ \begin{align} \int_0^1 dx &\int_0^{x^2} dy \frac{x^4}{x^5+1} \\[5pt] &= \frac{1}{2} \int_0^1 dx \frac{y^2}{x^5+1} \bigg|_0^{x^2} \\[5pt] &= \frac{1}{2} \int_0^1 dx \frac{x^4}{x^5+1} \end{align}$$
This is a good integral for u-substitution because of the difference of one in the powers of the numerator and denominator
$$ \begin{align} \text{Let } \; u &= x^5+1, \; \text{ then } \; du = 5x^4 \, dx \\[5pt] x &= 0 \; \rightarrow \; u = 1 \\[5pt] x &= 1 \; \rightarrow \; u = 2 \end{align}$$
Making the substitutions and changing the limits of integration gives
$$ \begin{align} \frac{1}{10} &\int_1^2 du \frac{1}{u} \\[5pt] &= \frac{1}{10} ln(u) \bigg|_1^2 \\[5pt] &= \frac{1}{10}(ln(2) - ln(1)) \\[5pt] &= \frac{ln(2)}{10} \end{align}$$
-
Calculate the double integral over region $R$, which is defined by the triangle in the $xy$-plane with vertices $(1, 1), (4, 1)$ and $(1, 2)$.
Solution
First let's have a look at the region, $R$.

The limits of integration in the y-direction are 1 (the lower limit) and $y = -\frac{1}{3}x + \frac{7}{3}$, the equation of the hypotenuse, which you can just obtain from the geometry of the problem. Then the limits in the $x$-direction are just 1 to 4. Here's the integral:
$$ \begin{align} \int_1^4 dx &\int_1^{-\frac{1}{3}x + \frac{7}{3}} dy \, (xy) \\[5pt] &= \int_1^4 dx \, \frac{xy^2}{2} \bigg|_1^{-\frac{1}{3}x} \\[5pt] &= \frac{1}{2} \int_1^4 dx \left[ x\left(-\frac{1}{3} x + \frac{7}{3}\right)^2 - \frac{x}{2} \right] \\[5pt] &= \frac{1}{2} \int_1^4 dx \left[ x \left( \frac{1}{9} x^2 - \frac{14}{9}x + \frac{49}{9} \right) - \frac{x}{2} \right] \\[5pt] &= \frac{1}{18} \int_1^4 dx \left[ x^3 - 14x^2 + 49x - \frac{x}{2} \right] \\[5pt] &= \frac{1}{18} \int_1^4 dx \left[ x^3 - 14x^2 - \frac{97}{2}x \right] \\[5pt] &= \frac{1}{18} \left[ \frac{x^4}{4} - \frac{14x^3}{3} - \frac{97x^2}{4} \right]_1^4 \end{align}$$
Now the rest is just arithmetic ... with plenty of opportunity to make mistakes:
$$ \begin{align} &\frac{1}{18} \left[ \frac{x^4}{4} - \frac{14x^3}{3} - \frac{97x^2}{4} \right]_1^4 \\[5pt] &= \frac{1}{18} \bigg[ \frac{4^4}{4} - \frac{14(4^3)}{3} - \frac{97(16)}{4} \\[5pt] &= \phantom{000} - \frac{1}{4} + \frac{14}{3} + \frac{97}{4} \bigg] &\dots = \frac{31}{8} \text{ units}^3 \end{align}$$
... where I've skipped some arithmetic steps that you can fill in if you feel so motivated.

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2024-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.