The vector cross product, $\vec{a} \times \vec{b}$
The cross product (also called the vector product), is a special product of two vectors in { $\mathbb{R}^3$ } space (3-dimensional $x,\; y,\; z$ space). The cross product of two 3-space vectors yields a vector orthogonal to the vectors being "crossed." It's one of the most important relationships between 3-D vectors. In this section we'll define the cross product and show how it works.
The symbol of the cross product is the 'times' symbol, ×. Generally there isn't much confusion between taking a cross product and vanilla multiplication because of the context. If a × comes between two vectors, we assume that means cross product.
Below we'll derive the cross product using the dot product, so if you need to, you might want to review that.
Derivation from the dot product
First, recall that the dot product between two vectors $\vec{a}$ and $\vec{b}$ yields the angle,$\theta$, between them:
$$\vec{a} \cdot \vec{b} = |a| |b| cos(\theta)$$
From here on I'll drop the arrows above vectors. It should be clear from the context when we're working with vectors. Now let's let the components of vectors $\vec a$ and $\vec b$ be
$$\vec a = (a_1, \; a_2, \; a_3)$$
and
$$\vec b = (b_1, \; b_2, \; b_3).$$
Let's also make a vector $n = (x, y, z)$ that will be the orthogonal vector (the vector perpendicular to $\vec a$ and $\vec b$) that we hope to construct. If $n$ is perpendicular to $\vec a$ and $\vec b$ then the dot products must equal zero:
$$ \begin{align} \vec a \cdot \vec n &= a_1 x + a_2 y + a_3 z = 0 \\[5pt] \vec b \cdot \vec n &= b_1 x + b_2 y + b_3 z = 0 \end{align}$$
Now we'll do a bit of manipulation to get where we want to go. Let's multiply the first dot product by $b_1$ and the second by $a_1$
$$ \begin{align} b_1(a_1 x + a_2 y + a_3 z) &= 0 \\[5pt] a_1(b_1 x + b_2 y + b_3 z) &= 0 \end{align}$$
Expanding these gives
$$ \begin{align} a_1 b_1 x + a_2 b_1 y + a_3 b_1 z &= 0 \\[5pt] a_1 b_1 x + a_1 b_2 y + a_1 b_3 z &= 0 \end{align}$$
Now subtract the second from the first to get a new equation. Notice that the first terms in each of the above equations, those containing $x$, are the same, so they'll go away.
$$a_2 b_1 y + a_3 b_1 z - a_1 b_2 y - a_1 b_3 z = 0$$
Now collect terms containing $y$ and $z$:
$$(a_2 b_1 - a_1 b_2) y + (a_3 b_1 - a_1 b_3) z = 0$$
Now move the second term to the right side:
$$(a_2 b_1 - a_1 b_2) y = (a_1 b_3 - a_3 b_1) z$$
Division by the quantities in parentheses give us an equality of ratios:
$$\frac{y}{a_1 b_3 - a_3 b_1} = \frac{z}{a_2 b_1 - a_1 b_2}$$
Now recall that our original choice of multiplication by $a_1$ and $b_1$ caused the terms with $x$ to vanish. We could easily have made another choice, dropping the $z$ term, for example, and found that
$$\frac{x}{a_2 b_3 - a_3 b_2} = \frac{y}{a_1 b_3 - a_3 b_1}$$
So we can equate all three like this:
$$\frac{x}{a_2 b_3 - a_3 b_2} = \frac{y}{a_1 b_3 - a_3 b_1} = \frac{z}{a_1 b_2 - a_2 b_1}$$
Now this equality is true if*
$$ \begin{align} x &= a_2 b_3 - a_3 b_2 \\[5pt] y &= a_1 b_3 - a_3 b_1 \\[5pt] z &= a_1 b_2 - a_2 b_1 \end{align}$$
These are the $\langle x, y, z \rangle$ coordinates of our vector that is orthogonal to vectors $\vec a$ and $\vec x$.
Properties of the cross product
Here are some key properties of the cross product that will come in handy when doing calculations. They can all be proved fairly easily using either the definition of 3-D cross product.
| Property | Explanation |
|---|---|
| $\vec{a} \times \vec{a} = -\vec{b} \times \vec{a}$ | The cross product is commutative to within a factor of -1 (i.e. it is not commutative, but predictably so). |
| $(k \vec{a}) \times \vec{b} = k (\vec{a} \times \vec{b}) = \vec{a} \times (k \vec{b})$ | where k is a constant. The outcome of a cross product is a vector. The multiplication by a constant need only be done once. |
| $\vec{a} \times (\vec{b} ± \vec{c}) = \vec{a} \times \vec{b} ± \vec{a} \times \vec{c}$ | The cross product is distributive over addition and subtraction |
| $(\vec{a} ± \vec{b}) \times \vec{c} = \vec{a} \times \vec{c} ± \vec{b} \times \vec{c}$ | The dot product is distributive as long as order is maintained (see above). |
| $\vec{a} \cdot (\vec{b} \times \vec{c}) = (\vec{a} \times \vec{b}) \cdot \vec{c}$ | Triple product |
| $\vec{a} \times (\vec{b} \times \vec{c}) = (\vec{a} \cdot \vec{c})\vec{b} - (\vec{a} \cdot \vec{b}) \vec{c}$ |
Example 1
Find the coordinates of the 3-D vector $\vec{z}$ that is orthogonal to $\vec{a} = (1, 0, 0)$ and $\vec{b} = (0, 1, 0)$.
Cross product
$$ \begin{align} x &= a_2 b_3 - a_3 b_2 = 0(1) - 1(0) = 0\\[5pt] y &= a_3 b_1 - a_1 b_3 = 1(0) - 0(0) = 0\\[5pt] z &= a_1 b_2 - a_2 b_1 = 1(1) - 0(0) = 1 \end{align}$$
So our orthogonal vector is $\vec{z} = (0, 0, 1)$ Think of vectors $\vec{a}$ and $\vec{b}$ as lying in the $x-y$ plane. Then our vector $\vec{z}$ is perpendicular (normal) to that plane, by definition of the 3-D Cartesian coordinate system.
Note that the vector $-\vec{z} = (0, 0, -1)$ is also normal to $\vec{a}$ and $\vec{b}$.

The cross product follows the right-hand rule
In example 1, we saw that there are actually two vectors orthogonal to $(1, \; 0, \; 0)$ and $(0, \; 1, \; 0)$. They are $(0, \; 0, \; 1)$ and $(0, \; 0, \; -1)$. By convention, we choose the first because it conforms to the right-hand rule.
The right-hand rule refers to a simple rule of thumb (so to speak) that pops up from time-to-time in math and especially physics. There are two versions
RHR version 1

In this version, we imagine that the $x$-vector (the first in $\vec{x} \times \vec{y}$) hinges at the origin and rotates into the $y$-vector. If the fingers of the right hand curve along the direction of that arcing route from $x$ to $y$, then the thumb points in the proper direction for the cross-product vector, upward in the diagram above.
RHR version 2

In this version of the RHR, the index finger, middle finger and thumb of the right hand are arranged so that each is about 90˚ from the others. Then if the index finger is pointed along the x-vector, and the middle finger along the y-vector, then the thumb points along the $\vec{x} \times \vec{y}$ vector.
You should really get to know one or both of these rules. They'll come in handy in future studies. If you're studying the cross product, you're well on your way there.
Example 2
Calculate the normalized vector orthogonal to $\vec{a} = \langle 1, 1, 1\rangle$ and $\vec{b} = \langle 1, \; 2, \; 3\rangle$. Recall that normalized means that the vector length is adjusted to one. That is, it is a unit vector.
The cross product (let's call it $\vec{c}$) is
$$ \begin{align} x &= a_2 b_3 - a_3 b_2 = 1(3) - 1(2) = 1\\[5pt] y &= a_3 b_1 - a_1 b_3 = 1(1) - 1(3) = -2\\[5pt] z &= a_1 b_2 - a_2 b_1 = 1(2) - 1(1) = 1 \end{align}$$
Now the length of this vector is $|c| = \sqrt{x^2 + y^2 + z^2}$, which is 6 units. In order to normalize vector $\vec c$, we divide all of its components by this length:
$$\vec{c}_N = \langle \frac{1}{6}, \frac{-2}{6}, \frac{1}{6} \rangle $$
The "N" subscript stands for "normalized." You can check for yourself that the length of our new vector is 1. And we can change the length of a vector without changing its direction, so this is the normalized vector orthogonal to $\vec{a} = \langle 1, \; 1, \; 1\rangle$ and $\vec{b} = \langle 1, \; 2, \; 3\rangle $.
A cross-product mnemonic
There is a handy way to remember how to calculate cross products involving the determinant of a 3-D matrix. If you need to review those, go here.
Let's say we're calculating the cross product of vectors $\vec{a} = \langle a_1, \; a_2, \; a_3\rangle $ and $\vec{b} = \langle b_1, \; b_2, \; b_3\rangle $. Our result vector will be vector $\vec{c} = \langle x, \; y, \; z\rangle $, where $x, \; y$ and $z$ are the unknown components of the cross product result. We begin by constructing a $3 \times 3$ matrix of these three row vectors like this:
$$\left( \begin{matrix} a_1 & a_2 & a_3 \\[5pt] b_1 & b_2 & b_3 \\[5pt] x & y & z \end{matrix} \right)$$
The cross product turns out to be the determinant of this matrix. You can find it by reproducing its first two columns to the right of the matrix, like this:
$$ \begin{array}{rrr|rr} a_1 & a_2 & a_3 & a_1 & a_2 \\[5pt] b_1 & b_2 & b_3 & b_1 & b_2\\[5pt] x & y & z & x & y \end{array}$$
Now the cross product can be calculated by following the diagonals in that matrix drawn below:

Using the diagonals, the x, y and z components of the cross product vector are the differences between the products indicated by the magenta diagonals and those indicated by the green diagonals. Thus we have
$$ \begin{align} x &= a_2 b_3 - a_3 b_2 \\[5pt] y &= a_3 b_1 - a_1 b_3 \\[5pt] z &= a_1 b_2 - a_2 b_1 \end{align}$$
3 × 3 determinants are fairly common, so if you can remember those, this is a nice way to remember the cross-product formulas.
The cross product is not commutative: $\vec{a} \times \vec{b} \ne \vec{b} \times \vec{a}$
We can use our determinant representation of the cross product to show that the cross product is not commutative. That is,
$$\vec{a} \times \vec{b} \ne \vec{b} \times \vec{a}$$
We already know the result of $\vec{a} \times \vec{b}.$ It is:

which gives
$$ \begin{align} x &= a_2 b_3 - a_3 b_2 \\[5pt] y &= a_3 b_1 - a_1 b_3 \\[5pt] z &= a_1 b_2 - a_2 b_1 \end{align}$$
If we swap $\vec{a}$ and $\vec{b}$ in our construction, we get:

which yields
$$ \begin{align} x &= a_3 b_2 - a_2 b_3 \\[5pt] y &= a_1 b_3 - a_3 b_1 \\[5pt] z &= a_2 b_1 - a_1 b_2 \end{align}$$
Notice that the second case is just the negative of the first for every component of vector $\vec c$. Thus we have:
$$\vec{a} \times \vec{b} = -[\vec{b} \times \vec{a}]$$
Recall that for vectors, $-1\cdot \langle x, \; y, \; z \rangle = \langle -x, \; -y, \; -z \rangle $.
Further, if you go back and review the right-hand rule, you'll notice that both cross products obey the rule because a swapping of vectors a and b results in a flipping of the direction of the thumb.
So while the cross product is not strictly commutative, it is to within a multiple of ±1 (change of sign). This kind of relationship is sometimes referred to as anti commutative.
Cross product as area of a parallelogram
The magnitude or length of the cross-product vector $\vec{a} \times \vec{b}$ turns out to be the area of the parallelogram defined by vectors $\vec{a}$ and $\vec{b}.$ Let's see how this comes about, and in the process, we'll discover a couple of new and useful formulas.

First consider the square of the cross product:
$$|\vec{a} \times \vec{b}|^2 = \left| \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\[4pt] a_1 & a_2 & a_3 \\[4pt] b_1 & b_2 & b_3 \end{matrix} \right|^2$$
Now that cross product is
$$(a_2 b_3 - a_3 b_2)^2 + (a_1 b_3 - a_3 b_1)^2 + (a_1 b_2 - a_2 b_1)^2,$$
where we recall that the square of a vector is the dot product of the vector with itself, e.g. $(a_1, a_2, a_3)^2 = a_1^2 + a_2^2 + a_3^2$. We've also eliminated the squares of the unit vectors $ \hat i$, $\hat j$, $\hat k$, as $( \, \hat{i} \,)^2 = 1,$ and so on. Now expanding those squared binomials, we get
$$= a_2^2 b_3^2 - 2 a_2 a_3 b_2 b_3 + a_3^2 b_2^2 + a_1^2 b_3^2 - 2 a_1 a_3 b_1 b_3 + a_3^2 b_1^2 + a_1^2 b_2^2 - 2 a_1 a_2 b_1 b_2 + a_2^2 b_1^2$$
Now if we're clever, we can reexpress this sum of terms like this:
$$= (a_1^2 + a_2^2 + a_3^2)(b_1^2 + b_2^2 + b_3^2) - (a_1 b_1 + a_2 b_2 + a_3 b_3)^2$$
Now we can recognize the first term as the square of the magnitude of $\vec{a},$ the second as the magnitude of $\vec{b},$ and the last as the square of the dot product, $\vec{a} \cdot \vec{b}:$
$$= |\vec{a}|^2 |\vec{b}|^2 - (\vec{a} \cdot \vec{b})^2$$
Inserting the definition of the dot product gives us
$$= |\vec{a}|^2 |\vec{b}|^2 - |\vec{a}|^2 |\vec{b}|^2 \cos^2(\theta),$$
where $\theta$ is the angle between vectors a and b. Factoring out the first term gives
$$= |\vec{a}|^2 |\vec{b}|^2(1 - \cos^2(\theta))$$
So finally, we have
$$|\vec{a} \times \vec{b}|^2 = |\vec{a}|^2 |\vec{b}|^2 \sin^2(\theta),$$
and thus
$$|\vec{a} \times \vec{b}| = |\vec{a}| |\vec{b}| \sin(\theta).$$
Here's a diagram showing how this represents the area of our parallelogram, the length of the base multiplied by the height, which is $h = |\vec{a}|\sin(\theta).$

This can be a very useful way to visualize a cross product, and it's worth keeping in mind.
The triple product
We can take the area-of-parallelogram idea a step further and use the cross and dot products to find the volume of a parallelepiped, a 3-dimensional parallelogram. Here's a picture of a parellelepiped (think "parallel + e'·pee·ped") formed from three vectors, $\vec{a}, \, \vec{b},$ and $\vec{c}:$

We already know that the magnitude of the cross product of two vectors (the blue vectors $\vec b$ and $\vec c$ in the figure above) gives the area of the parallelogram they define. The triple product is the dot product of that cross product vector (not its magnitude) with a third vector not in the same plane. (It could be in the same plane, but then the volume would be zero, and we're not interested in that).
From the figure, we can see that the volume of the parallelepiped is the area of its base, $|\vec{a} \times \vec{b}|,$ multiplied by the height, $h = |\vec{c}| cos(\theta),$ where $\theta$ is the angle between $\vec{c}$ and the base. Notice that the black vector is normal to the plane defined by $\vec b$ and $\vec c$.
$$V = |\vec{a} \times \vec{b}||\vec{c}| \cos(\theta)$$
Now this is just the definition of the dot product,
$$V = (\vec{a} \times \vec{b}) \cdot \vec{c}.$$
The dot product is commutative $(\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}),$ so this triple product is the same as
$$V = \vec{c} \cdot (\vec{a} \times \vec{b}).$$
With an eye toward showing another method for calculating the volume of a parallelepiped, let's do the triple product using the vector components:
$$ \begin{align} \vec a &= (a_1, a_2, a_3) \\[5pt] \vec b &= (b_1, b_2, b_3) \\[5pt] \vec c &= (c_1, c_2, c_3) \end{align}$$
The triple product is:
$$ \begin{align} (\vec a &\times \vec b) \cdot \vec c = \text{det} \left( \begin{matrix} i & j & k \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{matrix} \right) \cdot (c_1, c_2, c_3) \\[5pt] &= i(a_2 b_3 - a_3 b_2) + j(a_3 b_1 - a_1 b_3) + \\[5pt] &\phantom{000} (a_1 b_2 - a_2 b_1) \cdot (c_1, c_2, c_3) \\[5pt] &= (a_2b_3-a_3b_2, a_3b_1 - a_1b_3, a_1 b_2 - a_2 b_1) \cdot (c_1, c_2, c_3) \\[5pt] &= a_2b_3c_1 - a_3b_2c_1 + a_3b_1c_2 - a_1b_3c_2 + a_1b_2c_3 - a_2b_1c_3 \\[5pt] \end{align}$$
This is the same result as the determinant of the $3 \times 3$ matrix formed fromt the three row vectors of $\vec a, \; \vec b$ and $\vec c$:
$$ \left| \begin{matrix} a_1 & a_2 & a_3 \\[5pt] b_1 & b_2 & b_3 \\[5pt] c_1 & c_2 & c_3 \end{matrix} \right|$$
One last thing (optional): Cross product by minors of a matrix
There is one more way to calculate the cross product of two $\mathbb{R}^3$ vectors. It's still the determinant of the $3\times 3$ matrix
$$ \left( \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\[4pt] a_1 & a_2 & a_3 \\[4pt] b_1 & b_2 & b_3 \end{matrix} \right)$$
Here's the idea of minors.

To calculate the determinant, in terms of its $\hat{i}, \hat{j}, \hat{k}$ components, for minor matrices from our 3×3. The ith component is calculated by blocking out the ith row and column. The resulting 2×2 matrix that is not shaded is our minor. The ith component is
$$\hat{i} \left| \begin{matrix} a_2 & a_3 \\[4pt] b_2 & b_3 \end{matrix} \right|,$$
where the determinant of the 2×2 matrix is easy. Doing the same thing for the jth and kth components, (and incorporating a necessary sign change that I won't cover here) is
$$\vec{a} \times \vec{b} = \\[4pt] \hat{i} \left| \begin{matrix} a_2 & a_3 \\[4pt] b_2 & b_3 \end{matrix} \right| - \hat{j} \left| \begin{matrix} a_1 & a_3 \\[4pt] b_1 & b_3 \end{matrix} \right| + \hat{k} \left| \begin{matrix} a_1 & a_2 \\[4pt] b_1 & b_2 \end{matrix} \right|$$
Notice the minus operation in front of the $\vec{j}$ component. This can be a quick way of reliably calculating cross products, another tool in your matrix toolkit.
Practice problems
-
Normalize these vectors:
- $\vec{a} = \langle 2, 2, 3 \rangle $
- $\vec{v} = \langle -1, -1, -2 \rangle $
- $\vec{z} = \langle 0, 0, 3 \rangle $
Solutions
First calculate the lengths each vector:
$$ \begin{align} |\vec{a}| &= \sqrt{2^2 + 2^2 + 3^2} \\[5pt] &= \sqrt{17} \\[5pt] |\vec{v}| &= \sqrt{(-1)^2 + (-1)^2 + (-2)^2} \\[5pt] &= \sqrt{6} \\[5pt] |\vec{z}| &= \sqrt{0^2 + 0^2 + 3^2} \\[5pt] &= \sqrt{9} = 3 \\[5pt] \end{align}$$
Now divide each component of the vector by its length:
$$ \begin{align} \vec{a}_N &= \left( \frac{2}{\sqrt{17}}, \frac{2}{\sqrt{17}}, \frac{3}{\sqrt{17}} \right) \\[5pt] \vec{v}_N &= \left( \frac{-1}{\sqrt{6}}, \frac{-1}{\sqrt{6}}, \frac{-2}{\sqrt{6}} \right) \\[5pt] \vec{z}_N &= \left( 0, 0, \frac{3}{3} \right) = (0, 0, 1)\\[5pt] \end{align}$$
-
Calculate these cross products and normalize the resulting vector. Verify that it is orthogonal to both vectors:
- $(1, 1, -2) \times (2, 2, 3)$
- $(1, -6, 4) \times (2, -1, -1)$
- $(-1, -1, 3) \times (4, 6, -2)$
Solution
(a)
$$(1, 1, -2) \times (2, 2, 3) = \\[5pt] \hat{i} \left| \begin{matrix} 1 & -2 \\[5pt] 2 & 3 \end{matrix} \right| - \hat{j} \left| \begin{matrix} 1 & -2 \\[5pt] 2 & 3 \end{matrix} \right| + \hat{k} \left| \begin{matrix} 1 & 1 \\[5pt] 2 & 2 \end{matrix} \right|$$
$$= (7, 7, 0) \\[5pt] = \left( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}, 0 \right)$$
(b)
$$(1, -6, 4) \times (2, -1, -1) = \\[5pt] \hat{i} \left| \begin{matrix} -6 & 4 \\[5pt] -1 & -1 \end{matrix} \right| - \hat{j} \left| \begin{matrix} 1 & 4 \\[5pt] 2 & -1 \end{matrix} \right| + \hat{k} \left| \begin{matrix} 1 & -6 \\[5pt] 2 & -1 \end{matrix} \right|$$
$$= (10, 9, 11) \\[5pt] = \left( \frac{10}{\sqrt{302}}, \frac{9}{\sqrt{302}}, \frac{11}{\sqrt{302}} \right)$$
(c)
$$(-1, -1, 3) \times (4, 6, -2) = \\[5pt] \hat{i} \left| \begin{matrix} -1 & 3 \\[5pt] 6 & -2 \end{matrix} \right| - \hat{j} \left| \begin{matrix} -1 & 3 \\[5pt] 4 & -2 \end{matrix} \right| + \hat{k} \left| \begin{matrix} -1 & -1 \\[5pt] 4 & 6 \end{matrix} \right|$$
$$= (-16, 10, -2) \\[5pt] = \left( \frac{-8}{3\sqrt{20}}, \frac{5}{3\sqrt{20}}, \frac{-1}{3\sqrt{20}} \right)$$
These were done using the method of minors. You can, of course, get the same results by using the method of your choice. Give it a try.
-
Find the normalized vector orthogonal to $\vec{a} = (1, 3, 7)$ and $\vec{b} = (2, -1, 1)$.
Solution
We'll use the 3×3 matrix determinant form of the cross product:
$$ \begin{matrix} a_1 & a_2 & a_3 & a_1 & a_2 \\[5pt] b_1 & b_2 & b_3 & b_1 & b_2 \\[5pt] x & y & z & x & y \end{matrix}$$
which gives:
$$ \begin{matrix} 1 & 3 & 7 & 1 & 3 \\[5pt] 2 & -1 & 1 & 2 & -1 \\[5pt] x & y & z & x & y \end{matrix}$$
So our components are:
$$ \begin{align} x &= 3(1) - 7(-1) = 10 \\[5pt] y &= 7(2) - 1(1) = 13 \\[5pt] z &= 1(-1) - 3(2) = -7 \end{align}$$
The length of our new vector (we'll call it $\vec{c}$) is
$$|\vec{c}| = \sqrt{10^2 + 13^2 +(-7)^2} = \sqrt{318}$$
Finally, our normalized vector is
$$\vec{c}_N = \left( \frac{10}{\sqrt{318}}, \frac{13}{\sqrt{318}}, \frac{-7}{\sqrt{318}} \right)$$
-
Confirm that the unit vectors $\vec{x} = (1, 0, 0),$ $\vec{y} = (0, 1, 0)$ and $\vec{z} = (0, 0, 1)$ form an orthogonal set of basis vectors in 3-D space.
Solution
We need to show that each vector is the cross product of the other two. Here is one example.
$$ \begin{align} \vec{x} &\times \vec{y} \\[5pt] &= [0(0) - 1(0)]x + [0(0)- 1(0)]y + [1(1) - 0(0)]z \\[5pt] &= (0, 0, 1) = \vec{z} \end{align}$$
You can confirm the other two on your own.
Note that we could also have calculated the dot product between all three pairs and found that the angle between them is 90˚
-
Find a vector that is perpendicular to the plane determined by the points $P = (1, 2, 3)$, $Q = (-1, -1, 2)$ and $R = (0, 2, -1)$.
Solution
First we need to find two vectors in that plane. We can do that by subtracting the components of one vector (let's choose p) from the other two. That will give us two vectors with the same origin. Here are our three points plotted on a 3-D Cartesian grid:
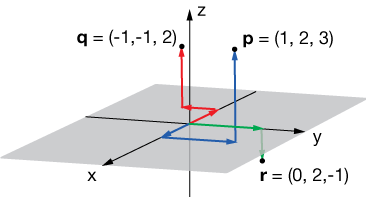
$$ \begin{align} \vec{Q} &= (-1 - 1, -1 - 2, 2 - 3) \\[5pt] &= (-2, -3, -1) \\[5pt] \vec{R} &= (0 - 1, 2 - 2, -1 - 3) \\[5pt] &= (-1, 0, -4) \end{align}$$
Here are our two new vectors R and Q that form the plane shown with the triangle.
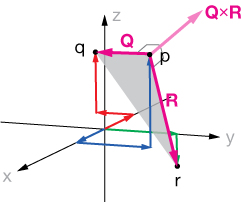
Now we find the cross product of those two vectors.
The
$$ \begin{matrix} a_1 & a_2 & a_3 & a_1 & a_2 \\[5pt] b_1 & b_2 & b_3 & b_1 & b_2 \\[5pt] x & y & z & x & y \end{matrix}$$
which gives:
$$ \begin{matrix} -2 & -3 & -1 & -2 & -3 \\[5pt] -1 & 0 & 4 & -1 & 0 \\[5pt] x & y & z & x & y \end{matrix}$$
So our components are:
$$ \begin{align} x &= -3(4) - (-1)0 = -12 \\[5pt] y &= -1(-1) - 4(-2) = 9 \\[5pt] z &= -2(0) - (-3)(-1) = -3 \end{align}$$
So our vector is
$$(-12, 9, -4)$$
These vectors can be difficult to visualize, but if you look at the plot above, our cross-product vector seems about right.
-
Calculate the volume of the parallelepiped determined by the vectors $\vec a, \; \vec b$ and $\vec c$.
-
$\vec a = (1, 2, 3), \; \vec b = (-1, 0, 2), \; \vec c = (2, 1, 4)$
Solution
The volume of a parallelepiped is the triple product $(\vec a \times \vec b) \cdot \vec c$. Here's the cross-product part:
$$ \begin{matrix} \hat i & \hat j & \hat k & \hat i & \hat j \\[5pt] 1 & 2 & 3 & 1 & 2 \\[5pt] -1 & 0 & 2 & -1 & 0 \end{matrix}$$
$$= 4\hat i -3\hat j + 0 + 2\hat k - 0 -2\hat j = 4\vec i -5\vec j + 2 \hat k$$
Now the absolute value of the dot product of $(4, -5, 2)$ with vector $\vec c$ give us our volume:
$$ \begin{align} |(4, -5, 2)\cdot (2, 1, 4)| &= |4(2) - 5(1) + 2(4)| \\[5pt] &= |8 - 5 + 8| \\[5pt] &= 11 \; \text{ units}^3 \end{align}$$
-
$\vec a = \vec i + \vec j, \; \vec b = \vec j + \vec k, \; \vec c = \vec i + \vec j - \vec k$
Solution
The volume of a parallelepiped is the triple product $(\vec a \times \vec b) \cdot \vec c$. Here's the cross-product part:
$$ \begin{matrix} \hat i & \hat j & \hat k & \hat i & \hat j \\[5pt] 1 & 1 & 0 & 1 & 1 \\[5pt] 0 & 1 & 1 & 0 & 1 \end{matrix}$$
$$= \vec k + \vec i + 0 - 0 - \vec j - 0$$
Now the dot product of $(1, -1, 1)$ with vector $\vec c$ give us our volume:
$$ \begin{align} |(1, -1, 1)\cdot (1, 1, -1)| &= |1(1) - 1(1) - 1(1)| \\[5pt] &= |1 - 1 - 1| \\[5pt] &= |-2| = 2 \; \text{cubic units} \end{align}$$
-
Orthogonal
In two dimensions, orthogonal means perpendicular. But when we proceed to three or more dimensions, "perpendicular" isn't good enough. In 3-D a line and a plane can be perpendicular when viewed from one direction, but not perpendicular when viewed from an angle 90˚ away on the plane. The word orthogonal means perpendicular in every conceivable direction, no matter how many dimensions.

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.