The big idea
Here's a nice analogy by Dr. Trefor Bazett, a mathematics professor at the University of Victoria, Canada (by the way, his calculus videos on YouTube are excellent).

Imagine that you have a field of snowdrifts like the one pictured here. That will be our three-dimensional function $z = f(x,y)$ where $(x,y)$ are coordinates on the ground and $z=f(x,y)$ gives the depth of the snow at each location. Now imagine we want to walk through that snowfield, shoveling a path as we go. Clearly, the total amount of snow we shovel will depend on the path we take. We could go straight through, take a longer, loopier path that avoids the deepest snow, or choose to meander through the peaks to shovel the most snow possible. There are endless possibilities.
In this section we'll learn how to "walk" along or traverse any path and add up the function above (or below) that path as we go.
Necessary digression: Parameterization is crucial
In order to do line integrals, we'll have to parameterize both the path and the function being integrated in terms of one or more parameters — one for linear or curved paths, two for surfaces, which we'll do later.
Let's recall some key methods of parameterization, keeping in mind that practice will be the key.
Linear paths
Let's say we want to perform a line integral along the line beginning at $(1, 2)$ and ending at $(5, 9)$. Recall that to parameterize a line we need a vector pointing to some point on it (usually one end is most convenient) — we'll call that $\vec r_o$, and a direction vector pointing along the line, and which will be multiplied by the parameter. Here's a picture:
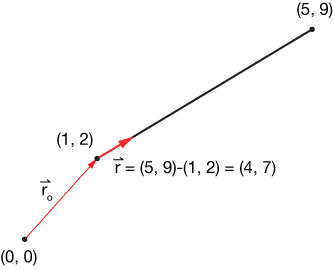
The direction vector is
$$ \begin{align} \vec r &= (5,9) - (1,2) \\[5pt] \vec r &= (5-1, \; 9-2) \\[5pt] \vec r &= (4,7) \end{align}$$
Now to reach any point on the segment (or really on the line of which it is a part) we have an equation
$$L = (1, 2) + t (4, 7)$$
where $\vec r_o$ is where we begin and $t$ is a parameter that determines the number of lengths of the direction vector $\vec r = (4, 7)$ to move on the line to get to our point, $(x, y)$.
$$ \begin{align} x &= 1 + 4t \\[5pt] y &= 2+7t \end{align}$$
Often the direction vector is normalized, but that won't be crucial in evaluating line integrals.
Curved paths
As a simple example, suppose we wanted to integrate over the path formed by $y = x^2$ between $(-1,1)$ and $(1,1)$. One parameterization could be to set $x=t$, then $y=t^2$, and the limits of $t$ would be $-1 \lt t \lt 1$. We could also set $y=t$, then $x=\sqrt{t}$, and so on. In this graph we've used the first parameterization. Notice that as the parameter (often interpreted as time) grows, we move along the curve from right to left

Paramaterizations are directional
Other coordinate systems
Some paths have circular symmetry, so it will be handy to be able to parameterize a function $f(x,y)$ in terms of a radial parameter, $r$, and an angle $\theta$. For example, if our path is the unit circle
$$x^2+y^2=1$$
we can use the parameterization
$$ \begin{align} x &= r \, \text{cos}(\theta) \\[5pt] y &= r \, \text{sin}(\theta) \\[5pt] r^2 &= x^2 + y^2 \end{align}$$
We'll do some examples using this kind of parameterization later. There are all kinds of ways to parameterize a function, and there is no unique parameterization of any function or curve.
The line integral
Here's the basic idea of the line integral. Imagine that we have some 3D function, $f(x,y)$, shown here as an upward-opening paraboloid — but it could be any continuous function. Then we have a path of some kind in the $xy$ plane, labeled $C$ in the graph. According to our original analogy, the $f(x,y)$ is our snowfield and $C$ our path through it.
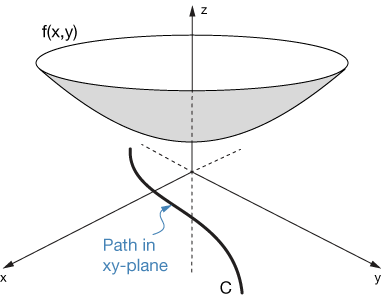
The integral we seek is the area of the curved surface above path $C$ and below $f(x,y)$. Just like any 1D integral, we should remember that part or all of $f(x,y$ could be under the $xy$ plane, possibly yielding a negative area.

In order to do this integral, we'll divide the region into rectangles in the usual way. The height of each rectangle will be approximately equal to the function value at one of its sides (recall that it doesn't matter which, because we'll be shrinking the widths of the rectangles and employing the mean-value theorem).
Here's a snapshot of how we'll break the vertical area over our path into rectangles — or trapezoids — it doesn't matter which.

And here's a zoomed in version of one of those trapezoids:
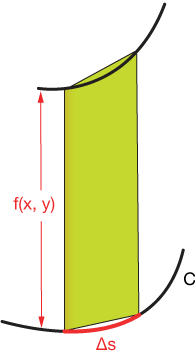
The dimensions of our rectangle are the height of the function $f(x,y)$ on one side (doesn't matter which), and the width is the arc length, $\Delta S$, which we can approximate by a line. Take a look at the zoomed-in picture of the bottom of the rectangle:
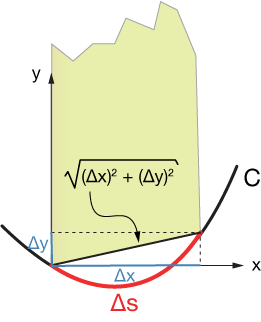
We can approximate $\Delta S$ by the straight-line distance across, $\Delta S \approx \sqrt{(\Delta x)^2 + (\Delta y)^2}$. So the approximate area of the ith rectangle is
$$\Delta A_i = f(x_i,y_i) \sqrt{(\Delta x)^2 + (\Delta y)^2}$$
Now we employ a trick: Divide and multiply each term under the radical by $\Delta t$:
$$\Delta A_i = f(g(t),h(t)) \sqrt{ \left(\frac{\Delta x}{\Delta t}\right)^2 + \left(\frac{\Delta y}{\Delta t}\right)^2 } \, \Delta t$$
Now recognize that in the limit of infinitely-narrow rectangles,
$\frac{\Delta x}{\Delta t}$ becomes $\frac{dx}{dt}$. Then if we parameterize $f(x,y)$ in terms of $t$ we get
$$dA = f(g(t),h(t)) \sqrt{(g'(t))^2 + (h'(t))^2} \, dt$$
Here $x=g(t)$ and $y=h(t)$. The part under the radical is just our expression for arc length of a parameterized function. Integration of $dA$ with respect to the parameter gives us our line integral:
The line integral of a function
$$A = \int \limits_C f(g(t),h(t)) \, \sqrt{(g'(t))^2 + (h'(t))^2} \, dt$$
Note: Because of that root term, some of these integrals can be tricky to solve analytically. We'll find a few work-arounds for that as we move through our studies of line integrals and Green's theorem.
Example 1
Calculate the line integral of the function $f(x,y)=x^2+y^2+4$ over the line segment from $(1,2)$ to $(3,5)$ in the $xy$ plane.
$$ \begin{align} C &= (1, 2) + t[(3,5)-(1,2)] \\[5pt] &= (1,2) + t(2,3) \end{align}$$
That give us our parameterized $x$ and $y$ coordinates,
$$x = 1+2t \phantom{000} y = 2+3t$$
In what follows we'll use the function notation
$$x = g(t) = 1+2t \phantom{000} y = h(t) = 2+3t$$
Then looking ahead, we can calculate
$$(x'(t))^2 = 4 \phantom{000} (y'(t))^2 = 9$$
So the root term in the line integral is just $\sqrt{13}$. It's nice when those are just constant, more difficult when they aren't. The limits on $t$ will be $0 \le t \le 1$.
Now to parameterize the function. That's easy, we just plug in our parameterized versions of $x$ and $y$:
$$ \begin{align} f(x) &= x^2+y^2 \\[5pt] &= (1+2t)^2 + (2+3t^2) \\[5pt] &= 1 + 4t + 4t^2 + 4 + 12t + 9t^2 \\[5pt] &= 13t^2 + 16t + 5 \end{align}$$
Now we an put the integral together:
$$ \begin{align} A &= \int \limits_C f(g(t),h(t)) \, \sqrt{(g'(t))^2 + (h'(t))^2} \, dt \\[5pt] &= \sqrt{13} \int_0^1 [13t^2+16t+5] \, dt \\[5pt] &= \sqrt{13} \left[\frac{13t^3}{3}+8t^2+5t \right]_0^1 \\[5pt] &= \sqrt{13} \left[ \frac{13}{3}+8+5 \right] \\[5pt] &= \sqrt{13} \left[\frac{13+24+15}{3} \right] = \frac{52 \sqrt{13}}{3} \end{align}$$
Example 2
Calculate the line integral of the function $f(x,y) = 3x^2+2xy^2$ over the path $C$, which is the unit circle in the $xy$ plane.
$$ \begin{align} r &= 1 \\[5pt] x &= \text{cos}(\theta) \\[5pt] x &= \text{sin}(\theta) \end{align}$$
The arc-length portion of our line integral is determined first by finding the squares of teh derivatives of $x(y)$ and $y(t)$:
$$(x'(t))^2 + (y'(t))^2 = (-\text{sin}(\theta))^2 + (\text{cos}(\theta))^2 = 1$$
So the root term is just $1$.
The function transforms like this:
$$ \begin{align} f(x,y) &= 3x^2+2xy^2 \\[5pt] &= 3 \,\text{cos}^2(\theta) + 2 \, \text{cos}(\theta) \, \text{sin}^2(\theta) \end{align}$$
If we split the integral into two parts, the first is
$$ \begin{align} A_1 &= \int_0^{2\pi} 3 \, \text{cos}^2(\theta) \\[5pt] &= 3 \int_0^{2\pi} \frac{1+\text{cos}(2 \, \theta)}{2} \, d\theta \tag{1} \\[5pt] &= 3 \left[ \frac{\theta}{2} + \frac{1}{4} \text{sin}(2\theta) \right]_0^{2\pi} \\[5pt] &= 3 [\pi + 0] = 3\pi \end{align}$$
In equation (1), we used the power-reduction formula for $\text{cos}^2(\theta)$,
$$\text{cos}^2(\theta) = \frac{1+\text{cos}(2\theta)}{2}$$
The second integral can be done with u-substitution:
$$ \begin{align} A_2 &= 2 \int_0^{2\pi} \text{cos}(\theta)\, \text{sin}^2(\theta) \, d\theta \\[5pt] \text{Let } & u = \text{sin}(\theta), \; \rightarrow \; du = \text{cos}(\theta) \, d\theta \\[5pt] &\rightarrow 2\int u^2 \, du = \frac{1}{3}u^3 \\[5pt] &= 2 \left[ \frac{1}{3} \text{sin}^3(\theta) \right]_0^{2\pi} \\[5pt] &= 0 \end{align}$$
So the total value of the integral is $3\pi$.
Note: Although our path was circular, this was not a polar integral, thus we didn't need the whole $r \, dr \, d\theta$ thing. We recognized that our path had the form of a circle with a fixed radius, and therefore could be parameterized with the single parameter $\theta$.
Closed-path integrals — new notation
When our path closes on itself (forms a simple loop), we call it a closed path. In what's ahead, that will be an important feature of line integrals, so we'll introduce a symbol for it here.
$$\oint$$
Example 3
Evaluate $\int_C (2+xy^2) dS$, where $C$ is the upper half of the circle $x^2+y^2=4$.
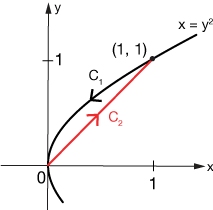
We'll take this integral in two pieces, moving in a counterclockwise (ccw) direction, as indicated by the arrows.
Path $C_1$
We can parameterize this path by setting $x = t$, then $y = t^2$. The limits will be $0 \le t \le 1$, and we'll integrate our function from $(1,1)$ to $(0,0)$.
The function transforms to
$$ \begin{align} 2 + xy^2 &= 2 + t \cdot (t^2)^2 \\[5pt] &= 2 + t^5 \end{align}$$
The derivatives of the path components are
$$ \begin{align} (x'(t))^2 &= 1 \\[5pt] (y'(t))^2 &= 4t^2 \end{align}$$
Our line integral is then
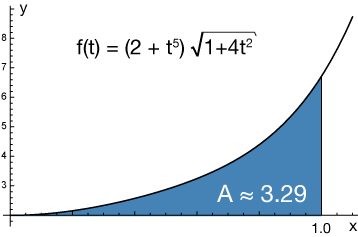
$$A = \int_1^0 (2+t^5) \sqrt{1+4t^2} \, dt$$
It doesn't take much fiddling with this integral to see that it's a difficult one. In fact, its solution involves a hyperbolic sine function (sinh). Done numerically on a calculator, it comes to $A_1 = -3.29$.
Path $C_2$
The parameterization of the line segment is
$$ \begin{align} L &= (1,1) + t(0-1,0-1) \\[5pt] &= (1,1) + t(-1,-1) \\[5pt] x &= 1-t \phantom{000} y = 1-t \end{align}$$
The limits on $t$ are $0 \le t \le 1$. The derivatives are
$$ (x'(t))^2 = 1 \phantom{000} (y'(t))^2 = 1$$
So the radical term in the integral is $\sqrt{2}$.
The function $f(x,y) = 2+xy^2$ transforms to
$$ \begin{align} f(g(t),h(t)) &= 2 + (1-t)(1-t)^2 \\[5pt] &= 2+ (1-t)(1-2t+t^2) \\[5pt] &= 2+ 1-2t+t^2-t+2t^2-t^3 \\[5pt] &= -t^3 + 3t^2 -3t +3 \end{align}$$
The line integral is
$$ \begin{align} A &= \sqrt{2} \int_0^1 (-t^3 + 3t^2 -3t +3) \, dt \\[5pt] &= \sqrt{2} \left[ \frac{-t^4}{4} + t^3 - \frac{3}{2}t^2 + 3t \right]_0^1 \\[5pt] &= \sqrt{2} \left[ -\frac{1}{4} + 1 - \frac{3}{2} + 3 \right] \\[5pt] &= \frac{9 \sqrt{2}}{4} = 3.18 \end{align}$$
Total area $\approx -0.11$
It may be a bit unnerving to have a negative area, but remember that just like in 1-D integration, some of the function may lie below the plane of any path we choose. A negative result is OK.
Line integrals with respect to $x$ and $y$
There is a particular class of line integrals for which we integrate along the $x-$ or $y-$directions only. If that's something you need to do, the integrals are simplified a little. They look like this:
$$ \begin{align} \int \limits_C f(x,y) \, dx = \int_a^b f(x(t),y(t)) \, x'(t) \, dt \\[5pt] \int \limits_C f(x,y) \, dy = \int_a^b f(x(t),y(t)) \, y'(t) \, dt \end{align}$$
These are really the same as our line integral formula above. The root term, which is the arc-length component of the integral, is
$$\sqrt{\left( \frac{dx(t)}{dt} \right)^2 + \left( \frac{dy(t)}{dt} \right)^2 }$$
In a line integral strictly along the x-axis, $\frac{dy(t)}{dt}$ is zero. Likewise for integrals along the y-direction, thus we end up with the formulas above. Given that for any integral,
We can also encounter integrals of the form
$$\int \limits_C f(x,y) \, dx + g(x,y) \, dy,$$
which can just be split into the relevant $dx$ and $dy$ line integrals and added back together.
Example 4
Evaluate $\int_C \, \left(\frac{1}{2} xy \, dy\right) \, dS$, where $C$ is the line segment between $(0, 0)$ and $(1, 2)$
Our integrand is
$$\frac{1}{2} t (2t) = t^2$$
What would be the radical part of our integral is just $y'(t) = 2$, so our integral is
$$ \begin{align} \int_0^1 2t^2 \, dt &= \frac{2}{3} t^3 \, \bigg|_0^1 \\[5pt] &= \frac{2}{3} \end{align}$$
Now just for drill, let's say we went the other way along our path, from $(1,2)$ to $(0,0)$. Then our parameterization would be $(1,2)+t(-1,-2)$ or $x = 1-t$ and $y=2-2t$ for $0 \le t \le 1$.
The integrand would be $\frac{1}{2}(1-t)(2-2t) = (1-t)^2 = 1-2t+t^2$. Multiplying by the derivative of $y$ gives
$$ \begin{align} -2\int_0^1 (1-2t+t^2) &= t -t^2+\frac{t^3}{3} \, \bigg|_0^1 \\[5pt] &= -2\left( 1-1-\frac{1}{3} \right) \\[5pt] &= \frac{-2}{3} \end{align}$$
This is just the negative of the first integral. If we switch directions along a path, the path integral switches signs.
Practice problems
Consider the list of vectors below, then use them to perform the following calculations.
-
Calculate $\int \limits_C (x-y) \, ds$, where $C$ is the line segment from $(1,3)$ to $(5,-2)$.
Solution
The parameterization of the path is
$$ \begin{align} C(t) &= (1, 3) + t(5-1,-2-3) \\[5pt] &= (1, 3) + t(4,-5) \\[5pt] 0 &\le t \le 1 \\[5pt] x &= 1+4t \phantom{000} y = 3-5t \end{align}$$
Our squared derivatives are
$$(x'(t))^2 = 16 \phantom{000} (y'(t))^2 = 25$$
So our root term is $\sqrt{41}$.
The integrand is
$$ \begin{align} x-y &= 1+4t - (3 - 5t) \\[5pt] &= 1-3+9t \\[5pt] &= 9t-2 \end{align}$$
The integral is:
$$ \begin{align} A &= \sqrt{41} \int_0^1 9t-2 \, dt \\[5pt] &= \sqrt{41} \left[ \frac{9t^2}{2} - 2t \right]_0^1 \\[5pt] &= \sqrt{41} \left[ \frac{9}{2} - 2 \right] \\[5pt] &= \frac{5 \sqrt{41}}{2} \end{align}$$
-
Calculate $\int \limits_C (z+y^2) \, ds$, where $C$ is the line segment from $(3,4,0)$ to $(1,4,2)$. (3D line integrals like this are a simple extension of the 2D integrals in the examples).
Solution
The path parameterization is
$$ \begin{align} C(t) &= (3,4,0) + t(1-3,4-4,2-0) \\[5pt] &= (3,4,0) + t(-2,0,2) \\[5pt] 0 &\le t \le 1 \\[5pt] x &= 3-2t, \phantom{00} y = 4, \phantom{00}, z = 2t \end{align}$$
Our squared derivatives are
$$(x'(t))^2 = 4, \; (y'(t))^2 = 0, \; (z'(t))^2 = 4,$$
which makes our root term $\sqrt{4+0+4} = 2 \sqrt{2}$
The integrand is
$$z + y^2 = 2t + 16$$
Our integral is
$$ \begin{align} 2 \sqrt{2} \int_0^1 2t&+16 \, dt \\[5pt] &= 2 \sqrt{2} \left[ t^2 + 16t \right]_0^1 \\[5pt] &= 2 \sqrt{2}[1+16] = 34 \sqrt{2} \end{align}$$
-
Calculate $\int \limits_C y \, ds$, where $C$ is the upper half of the circle of radius 3 from $(3,0)$ to $(-3,0)$.
Solution
Here's a picture of our path:
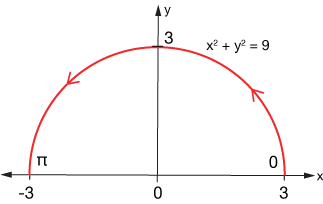
We'll take advanage of the symmetry and parameterize with the polar angle $\theta$.
$$ \begin{align} x(\theta) &= r \, \text{cos}(\theta) \\[5pt] y(\theta) &= r \, \text{sin}(\theta) \\[5pt] r(t) &= (3 \, \text{cos}(\theta), 3 \, \text{sin}(\theta)) \\[5pt] |r'(t)| &= \sqrt{9 \text{sin}^2(\theta) + 9 \text{cos}^2(\theta)} \\[5pt] &= 3 \end{align}$$
The integrand is just $y = 3 \, \text{sin}(\theta)$, so our integral is
$$ \begin{align} 3 \int_0^\pi 3 &\, \text{sin}(\theta) \, d\theta \\[5pt] &= 9 \left[-\text{cos}(\theta) \right]_0^{\pi} \\[5pt] &= -18 \end{align}$$
-
Evaluate the line integral $\int \limits_C (xy+z^3) \, ds$, where $C$ is the piece of the helix $\vec r(t) = (\text{cos}(t), \text{sin}(t), t)$ from $t=0$ to $t=\pi$.
Solution
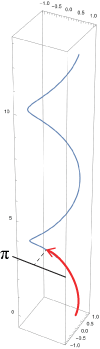
Here's the path for this integral.
It's a helix with a circular profile in the $xy$ plane as we look down the $z$-axis, and the $z$ component of $\vec r(t)$ gives the amount of rise or pitch of the helix as it turns.
Our path for this exercise is just the red portion.
We already have the parameterization of this path, so the squares of the derivatives are
$$ \begin{align} (x'(t))^2 &= \text{sin}^2(t) \\[5pt] (y'(t))^2 &= \text{cos}^2(t) \\[5pt] (z'(t))^2 &= 1 \end{align}$$
So the root term of our line integral is
$$\sqrt{\text{cos}^2(t) + \text{sin}^2(t) + 1} = \sqrt{2}$$
Our integrand is
$$xy+z^3 = \text{cos}(t) \text{sin}(t) + t^3$$
The integral is
$$ \begin{align} \sqrt{2}\int_0^{\pi} &\text{cos}(t) \text{sin}(t) + t^3 \, dt \\[5pt] &= \sqrt{2} \left[ \frac{1}{2} \text{sin}^2(t) + \frac{t^4}{4} \right]_0^{\pi} \\[5pt] &= \frac{\pi^4 \sqrt{2}}{4} \approx 34.4 \end{align}$$
-
The mass of a fine wire of variable density can be found by performing a line integral of the density function, $\delta$, over the curve of the wire. If the wire has the shape of the top part of a circle: $\sqrt{9-x^2}$ with $0 \le x \le 3$and its density function is $\delta(x,y) = x \sqrt{y}$, calculate the mass of the wire.
Solution
The path is the quarter of the circle of radius $r = 3$ centered at the origin and in the first quadrant, so we can parameterize it in terms of angle $\theta$, with $0 \le \theta \le \pi/2$. Then the integrand (the density function) transforms to
$$x \sqrt(t) = 3 \, \text{cos}(\theta) \sqrt{3 \text{sin}(\theta)}$$
The coordinates are $x(t) = 3 \, \text{cos}(\theta)$ and $y(t) = 3 \, \text{sin}(\theta)$. So the root term will just turn out to be $3$. The integral is:
$$ \begin{align} 9\sqrt{3} \int_0^{\pi/2} &\text{cos}(\theta) \sqrt{\text{sin}(\theta)} \, dt \\[5pt] \text{Let } u &= \text{sin}(\theta), \; du = \text{cos}(\theta) \, d\theta \\[5pt] 9\sqrt{3} &\int u^{1/2} du \\[5pt] &= 9\sqrt{3} \frac{2}{3} \text{sin}^{3/2}(\theta) \bigg|_0^{\pi/2} \\[5pt] &= 9\sqrt{3} \frac{2}{3} [1-0] = 6 \sqrt{3} \end{align}$$
-
Evaluate $\int \limits_C (y-x) \, dx + (xy) \, dy$ where $C$ is the line segment from $(2,4)$ to $(3,1)$.
Solution
Think of this as the sum of line integrals along the $x$- and $y$-axes, respectively. First parameterize the line segment:
$$ \begin{align} C(t) &= (2,4) + t(3-2, \; 1-4) \\[5pt] &= (2, 4) + t(1, -3) \\[5pt] x &= 2+t \phantom{000} y = 4-3t \end{align}$$
Now the two parts of our integrand are
$$ \begin{align} y - x &= 4-3t - (2+t) \\[5pt] &= 2 - 4t \\[5pt] xy &= (4-3t)(2+t) \\[5pt] &= 8+4t-6t-3t^2 \\[5pt] &= -3t^2-2t+8 \end{align}$$
Our derivatives are
$$\frac{dx}{dt} = 1 \phantom{0000} \frac{dy}{dt} = -3$$
Finally, the integral is
$$ \begin{align} \int_0^1 &(2-4t)(1) + (-3t^2-2t+8)(-3) \, dt \\[5pt] &= \int_0^1 2-4t+9t^2+6t-24 \, dt \\[5pt] &= \int_0^1 9t^2 +2t-22 \, dt \\[5pt] &= \left[ 3t^3 + t^2 -22t \right]_0^1 \\[5pt] &= 3+1-22 = -18 \end{align}$$
Cartesian coordinates
Cartesian coordinates are the normal 2-dimensional (2D) or 3-dimensional (3D) coordinate systems we most-frequently use. In two dimensions, we draw x- and y-axes at 90˚ angles to each other, and in 3D we add a third axis, usually the z-axis, perpendicular to the x-y plane.
The location or direction of an point or particle can be described using Cartesian coordinates (x, y) in the 2D plane, or (x, y, z) in 3D.
Parameter
A parameter is an adjustable constant in the definition of a function that is different from the independent variable(s). Parameters are not independent variables. For example, in the quadratic function
f(x) = Ax2 + Bx + C
A, B and C are parameters which change the shape of the graph of the function. x is the independent variable. A, B and C are fixed for any particular version of f(x), but x can range from -∞ to +∞

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.

