Headline
Let's begin with our derivatives in the $x$- and $y$-directions — the normal partial derivatives:
$$ \begin{align} D_{x} f(x_o, \; y_o) = \lim_{h \to 0} \frac{f(x_o+h, \; y_o) - f(x_o, \; y_o)}{h} \\[5pt] D_{y} f(x_o, \; y_o) = \lim_{h \to 0} \frac{f(x_o, \; y_o+h) - f(x_o, \; y_o)}{h} \\[5pt] \end{align}$$
These are the rates of change of our function in the $x$- and $y$ directions, respectively. Now we'd like to find the rate of change of $z$ at point $P = (x_o, \; y_o)$ in the direction of some other unit vector $\hat u = \langle a, \; b \rangle$.
Let's let $S$ be a surface with $z = f(x, \; y)$ and $z = f(x_o, \; y_o)$. Then point $P = (x_o, \; y_o, \; z_o)$ lies on surface $S$. The vertical plane passing through $P$ in the direction of $\hat u$ intersects $S$ in a curve, $C$. Here's the basic geometry:

Here is a blowup of the geometry shown in yellow dashed lines in the previous figure. The unit direction vector $\hat u = \langle a, \; b \rangle$. Any vector of lenth $h$ (a scalar) can be written as $h\hat u$ or $h \langle a, \; b \rangle$.
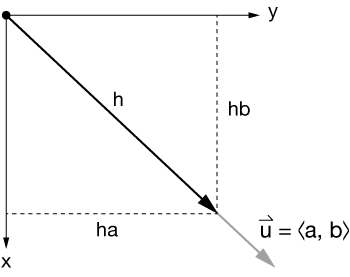
The slope of the tangent line, $T$ is the rate of change in the direction of $\hat u$. That's what we're after here. We can also write vector $h \hat u$ as
$$ \begin{align} \vec{P'Q'} &= \langle x-x_o, \; y-y_o, \; 0 \rangle \tag{1} \\[5pt] &= h \hat u = \langle ha, \; hb \rangle \tag{2} \end{align}$$
where $h$ is a scalar. We have then, by association between the vectors in $(1)$ and $(2)$,
$$ \begin{align} x - x_o = ha \; \longrightarrow x = x_o + ha \\[5pt] y - y_o = hb \; \longrightarrow y = y_o + hb \end{align}$$
Now we can construct an average slope in the $z$-coordinate like this:
$$\frac{\Delta z}{h} = \frac{z-z_o}{h} = \frac{f(x_o+ha, \; y_o+hb) - f(x_o,y_o)}{h}$$
Now we take the limit of this ratio as $h \to 0$ to get a derivative:
$$D_{\hat u} f(x_o,y_o) = \lim_{x\to 0} \frac{f(x+ha, y+hb) - f(x_o,y_o)}{h}$$
where $D_{\hat u}$ will be our new notation for the derivative of a function in the direction of vector $\hat u$.
Notice that if our direction vectors are $\hat u = \hat i = \langle 1, \; 0 \rangle$, or $\hat u = \hat j = \langle 0, \; 1 \rangle$, then our directional derivatives are $D_{\hat i}f = f_x$ and $D_{\hat j}f = f_y$, which are just our vanilla partial derivatives taken with respect to the $x$- and $y$-axes, respectively.
Now we'll propose and prove a theorem that will make calculating directional derivatives easy.
Theorem
If $f$ is a function of $x$ and $y$ that is differentiable over its range, then $f$ has directional derivatives in the direction of any unit vector $\hat u = \langle a, \; b \rangle$, and
$$D_{\hat u}f(x,y) = f_x(x,y) a + f_y(x,y) b$$
where $f_x$ and $f_y$ are partial derivatives.
Proof
First, let $g(h) = f(x_o+ha, \; y_o+hb)$. Then we have
$$ \begin{align} g'(0) &= \lim_{h\to 0} \frac{g(h)-g(0)}{h} \\[5pt] &= \lim_{h\to 0} \frac{f(x_o+ha, \; y_o+hb) - f(x_o, y_o)}{h} \\[5pt] &= D_{\hat u} f(x_o, \; y_o) \tag{1} \end{align}$$
We can also write
$$ \begin{align} g(h) &= f(x,y), \; \text{with} \\[5pt] x &= x_o + ha \\[5pt] y &= y_o + hb \end{align}$$
The chain rule then gives us
$$ \begin{align} g'(h) &= \frac{\partial f}{\partial x} \frac{\partial x}{\partial h} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial h} \\[5pt] &= f_x(x, y) a + f_y(x,y) b \end{align}$$
Now plug in $h=o$ to match equation $(1)$ above. When $h=0$ we have $x=x_o$ and $y = y_o$, so
$$g'(0) = f_x(x_o, y_o)a + f_y(x_o, y_o)b \tag{2}$$
Now $(1)$ and $(2)$ are the same, so we've proved our theorem.
$$D_{\hat u}f(x,y) = f_x(x,y) a + f_y(x,y) b$$
Example 1
Calculate the derivative of the function $z = x^2+y^2$ at point $P = (0, 2)$ in the direction of $\vec u = \langle 1, \; 4 \rangle$.
First we'll need the length of $\vec u$. It's $|\vec u| = \sqrt{2}$. Then our unit direction vector is
$$\hat u = \bigg< \frac{1}{\sqrt{17}}, \; \frac{4}{\sqrt{17}} \bigg>$$
The derivative is
$$ \require{cancel} \begin{align} D_{\hat u}f(x,y) &= f_x(x,y) a + f_y(x,y) b \\[5pt] &= 2x \left( \frac{1}{\sqrt{2}} \right) + 2y \left( \frac{1}{\sqrt{2}} \right) \\[5pt] &= \cancel{2(0) \left( \frac{1}{\sqrt{17}} \right)} + 2(2) \left( \frac{1}{\sqrt{17}} \right) \\[5pt] &= \frac{4}{\sqrt{17}} \approx 3.88 \end{align}$$
Here is a contour plot* of that same function, $f(x,y) = x^2+y^2$, drawn looking above, into the "bowl." The
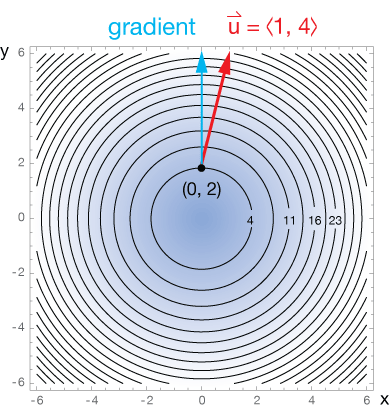
The uphill slope at $(0, \; 2)$ in the direction of $\hat u$ is $3.88$, while the steepest slope is along the blue vector, with a value of $4.0$. That steepest ascent is called the gradient. We'll encounter that just ahead.
* Think about a topographic map of mountains and valleys, where each curve on the map represents a constant height or altitude.
The gradient vector
Let's re-express the directional derivative in the direction of $\hat u = \langle a, \; b \rangle $ slightly:
$$ \begin{align} D_{\hat u} f(x,y) &= f_x(x,y)a + f_y(x,y)b \\[5pt] &= \langle f_x(x,y), \; f_y(x,y) \rangle \cdot \langle a, \; b \rangle \\[5pt] &= \langle f_x(x,y), \; f_y(x,y) \rangle \cdot \hat u \end{align}$$
We'll call the vector $\langle f_x(x,y), \; f_y(x,y) \rangle$ the gradient vector. We'll further define an "operator" called "del", with symbol $\nabla$ (called "nabla") as a pseudo-vector:
$$\nabla = \bigg< \frac{\partial}{\partial x}, \; \frac{\partial}{\partial y}\bigg>$$
The three-dimensional version is
$$\nabla = \bigg< \frac{\partial}{\partial x}, \; \frac{\partial}{\partial y}, \; \frac{\partial}{\partial z} \bigg>$$
We can use $\nabla$ in two ways. One is as an operator, which is just a set of instructions for what to do with another vector of the same dimensions. That is,
$$ \begin{align} \nabla f(x, y) &= \bigg< \frac{\partial f}{\partial x}, \; \frac{\partial f}{\partial y} \bigg> \\[5pt] \nabla f(x, y, z) &= \bigg< \frac{\partial f}{\partial x}, \; \frac{\partial f}{\partial y}, \; \frac{\partial f}{\partial z} \bigg> \end{align}$$
These are the gradient vectors of functions $f(x,y)$ and $f(x,y,z)$, respectively.
Or we can use $\nabla$ to stand for the gradient vector and take a dot product with another vector. For example if $\nabla f(x,y,x) = \langle a, \; b, \; c \rangle$ and $\vec v = \langle xy, \; yz, \; xz \rangle$, then
$$ \begin{align} \nabla \cdot \vec v &= \bigg< \frac{\partial}{\partial x}, \; \frac{\partial}{\partial y}, \; \frac{\partial}{\partial z} \bigg> \cdot \langle xy, \; yz, \; xz \rangle \\[5pt] &= y + z + x \end{align}$$
Here we took a strange dot product. For example the "product" of $\frac{\partial}{\partial x}$ with vector component $xy$ just means to take that partial derivative. It's a loosey-goosey notation, but it works and we'll use it a lot. Like all dot products, the result is a scalar. The gradient vector will turn out to point toward the direction of maximum slope and the dot
Gradient: Vector of steepest ascent
The gradient vector always points in the direction of steepest ascent.
Theorem
If $f$ is a differentiable function of two or three variables (represented by $\vec x$), the maximum value of the directional derivative in the direction of $\hat u$ is $|\nabla \cdot f(\vec x)|$. It occurs when $\hat u$ has the same direction as $\nabla f(\vec x)$.
Proof
$$ \begin{align} D_{\hat u} &= \nabla f(\vec x) \\[5pt] &= |\nabla f(\vec x)| |\hat u| \cos(\theta) \tag{1}\\[5pt] &= |\nabla f(\vec x)| \cos(\theta) \tag{2} \\[5pt] \end{align}$$
In equation $(1)$ we've used the dot product definition. In $(2)$ we recognize that the length of a unit vector is 1. Then the maximum of the expression in $(2)$ occurs when $\cos(\theta)$ has a maximum, and that's $\theta = 0$, which means that the angle between $\hat u$ and $\nabla f(\vec x)$ is zero — they are in the same direction.
The directional derivative
The directional derivative of the function $f$ in the direction of $\vec u$, which we write as $D_{\vec u} f$, is
$$D_{\vec u} f = \frac{\nabla f \cdot \vec u}{|\vec u |}$$
Recall that $\frac{\vec u}{|\vec u|}$ is just the normalized version of $\vec u$, which is $\hat u$.
Example 2
Consider the function $f(x,y) = 9-x^2-y^2$. Find the directional derivative in the direction of $\vec u = \langle 1, \; 2 \rangle$ over the point $P = (1, 1)$ in the $xy$ plane.
$$ \begin{align} \nabla f &= \bigg< \frac{\partial f}{\partial x}, \; \frac{\partial f}{\partial y} \bigg> \\[5pt] &= \langle -2x, \; -2y\rangle \\[5pt] \nabla f(1,1) &= \langle -2, \; -2\rangle \end{align}$$
The length of $\vec u$ is
$$| \vec u | = \sqrt{1^2 + 2^2} = \sqrt{5}$$
Now we can compute our directional derivative:
$$ \begin{align} D_{\vec u} f &= \frac{\nabla f \cdot \vec u}{\vec u} \\[5pt] &= \frac{\langle -2,-2\rangle \cdot \langle1, 2\rangle}{\sqrt{5}} \\[5pt] &= \frac{-2(1) - 2(2)}{\sqrt{5}} \\[5pt] &= -\frac{6}{\sqrt{5}} = -\frac{6 \sqrt 5}{5} \end{align}$$
Example 3
Find the directional derivative of $f(x,y) = (1+xy)^{3/2}$ at point $P = (3, 1)$ and in the direction $\vec u = \langle 1, 1\rangle $.
$$ \begin{align} \nabla f &= \bigg< \frac{\partial f}{\partial x}, \; \frac{\partial f}{\partial y} \bigg> \\[5pt] &= \bigg< \frac{3}{2} y \sqrt{1 + xy}, \; \frac{3}{2} x \sqrt{1 + xy} \bigg> \\[5pt] \nabla f(3,1) &= \langle 3, \; 9 \rangle \end{align}$$
Let $\vec u = \langle 1, \; 1\rangle = \hat i + \hat j$. Then the length of $\vec u$ is
$$| \vec u | = \sqrt{1^2 + 1^2} = \sqrt{2}$$
Now we can compute our directional derivative:
$$ \begin{align} D_{\vec u} f &= \frac{\nabla f \cdot \vec u}{\vec u} \\[5pt] &= \frac{\langle 3,9\rangle \cdot \langle 1, 1\rangle}{\sqrt{2}} \\[5pt] &= \frac{3(1) + 9(1)}{\sqrt{2}} \\[5pt] &= \frac{12}{\sqrt{2}} = 6 \sqrt{2} \end{align}$$
Example 4
Let's do an example with three independent variables — it's the same idea. Find the derivative of $f(x,y,z) = x^2+2y^2+3z^2$ at point $P_o = (3,2,1)$ along the direction $\vec u = \langle 2, \; 1, \; 1\rangle $.
$$\hat u = \frac{\langle 2,1,1 \rangle}{\sqrt{2^2+1^2+1^2}} = \frac{1}{\sqrt{6}}\langle 2,1,1\rangle $$
The gradient of $f(x,y,z)$ is
$$\nabla f(x,y,z) = \langle 2x,4y,6z\rangle$$
Now the directional derivative is
$$ \begin{align} \nabla f(x,y,z) \cdot \hat u &= \langle 2x,4y,6z \rangle \cdot \langle 2,1,1\rangle \frac{1}{\sqrt{6}} \\[5pt] &= \frac{1}{\sqrt{6}} (4x+4y+6z) \end{align}$$
Then we plug in our point, $P_o$:
$$ \begin{align} D_{\hat u}\langle 3,2,1\rangle &= \frac{1}{\sqrt{6}} (4x+4y+6z) \\[5pt] &= \frac{1}{\sqrt{6}} [4(3)+4(2)+6(1)] \\[5pt] &= \frac{12}{\sqrt{6}} + \frac{8}{\sqrt{6}} + \frac{6}{\sqrt{6}} \\[5pt] &= \frac{26}{\sqrt{6}} \end{align}$$
Example 5
Suppose that the temperature, $T$ at point $(x,y,z)$ of a block of metal is given by
$$T = \frac{30}{1+3x^2+2y^2+z^2}$$
with $T$ in $^{\circ}C$, and $x, \; y, \; z$ in meters. In which direction does $T$ increase fastest at point $(1, \; 1, \; 2)$ ?
$$ \begin{align} \nabla T &= \bigg< \frac{\partial T}{\partial x}, \; \frac{\partial T}{\partial y}, \; \frac{\partial T}{\partial z} \bigg> \\[5pt] &= \bigg< \frac{-180x}{(1+3x^2+2y^2+z^2)^2}, \; \frac{-120y}{(1+3x^2+2y^2+z^2)^2}, \; \frac{-60x}{(1+3x^2+2y^2+z^2)^2} \bigg> \\[5pt] \nabla T_{(1, 1, -2)} &= \bigg< \frac{-180}{7}, \; \frac{-120}{7}, \; \frac{120}{25} \bigg> \\[5pt] &\approx \langle -25.7, -17.1, \; 4.8 \rangle \end{align}$$
The length of the gradient vector is the value of the slope, which is $31.24^{\circ}C/m$.
Practice problems
Find an equation of the plane tangent to the surface at the given point.
-
For $f(x,y) = 4 - x^2 - y^2$, calculate the derivative of $f$ above point $(1, 1)$ in the $x-y$ plane and along the vector $\vec u = \langle 1, 3 \rangle $. What does it mean that $\nabla f(0, 0) = \vec 0$ for this function?
Solution
First calculate the unit vector form of $\vec u$:
$$ \begin{align} |\vec u| &= \sqrt{1^2 + 3^2} = \sqrt{10} \\[5pt] \hat u &= \frac{1}{\sqrt{10}} (1, 3) \end{align}$$
Now $\nabla f = (-2x, -2y)$, so
$$ \begin{align} \nabla f \cdot \hat u &= (-2x, -2y) \cdot (1, 3) \frac{1}{\sqrt{10}} \\[5pt] &= \frac{-2x}{\sqrt{10}} - \frac{6y}{\sqrt{10}} \end{align}$$
Finally,
$$\nabla f \cdot \hat u(1, 1) = \frac{-2}{\sqrt{10}} - \frac{6}{\sqrt{10}} = \frac{-8}{\sqrt{10}}$$
This makes sense because the function is a downward-opening paraboloid, which we'd expect to have a negative slope in this direction. The gradient of the function, $\nabla f(0,0) = (0, 0)$, the zero vector. This is because $(0,0)$ is the global maximum value of the function.
-
Find the directional derivative of $f(x,y) = sin(xy^2)$ above point $P = (\pi/4, 2)$ in the direction of $\vec u = \langle 1, 1\rangle $
Solution
The unit direction vector is
$$\hat u = \frac{1}{\sqrt{2}}(1, 1)$$
The gradient vector is
$$\nabla f = (y^2\cos(xy^2), 2xy \, \cos(xy^2))$$
Then we have
$$ \begin{align} \nabla f &= (y^2\cos(xy^2), 2xy \, \cos(xy^2)) \cdot (1,1) \frac{1}{\sqrt{2}} \\[5pt] &= \frac{1}{\sqrt{2}} \left[ y^2 \cos(xy^2) + 2xy \, \cos(xy^2) \right] \end{align}$$
Finally,
$$ \require{cancel} \begin{align} \nabla f &\left( \frac{\pi}{4}, 2 \right) \cdot \hat u \\[5pt] &= \frac{1}{\sqrt{2}} \left[ 4 \cos(\pi) + \cancel{2} \left(\frac{\pi}{\cancel{4}} \right)\cancel{2} \cos(\pi) \right] \\[5pt] &= \frac{1}{\sqrt{2}} \left[ (4 + \pi) \cos(\pi) \right] \\[5pt] &= -\frac{1}{\sqrt{2}} (4 + \pi) \\[5pt] &= \frac{-(4+\pi)}{\sqrt{2}} \end{align}$$
-
Find the derivative of $f(x,y) = x^2 + xy + y^2$ above point $P = (0, 1)$ in the direction of $-3 \hat i + 4 \hat j$.
Solution
The unit vector version of $\vec u$ is
$$ \begin{align} |\vec u| &= \sqrt{(-3)^2+4^2} = \sqrt{25} = 5 \\[5pt] \rightarrow \; \hat u &= \frac{1}{5}(-3, 4) \end{align}$$
The gradient is
$$\nabla f(x,y) = (2x + y, 2y + x)$$
$$ \begin{align} \nabla f \cdot \hat u &= -\frac{3}{5}(2x + y) + \frac{4}{5} (2y + x) \\[5pt] &= -\frac{6}{5} x - \frac{3}{5} y + \frac{8}{5} y + \frac{4}{5} x \\[5pt] &= -\frac{1}{5} x + y \end{align}$$
Then
$$\nabla f(0, 1) \cdot \hat u = -\frac{1}{5} (0) + 1 = 1$$
-
Find the derivative of $f(x,y,z) = (x-y)(y-z)(z-x)$ above point $P = (1,1,1)$ in any direction.
Solution
It will be easier to find the gradient (take the derivatives) if we expand these binomials:
$$ \begin{align} f(x,y,z) &= (x-y)(y-z)(z-x) \\[5pt] &= (xy - xz - y^2 + yz)(z-x) \\[5pt] &= \cancel{xyz} - x^2 y - xz^2 + x^2z \\[5pt] &\phantom{000} - y^2z + xy^2 + yz^2 - \cancel{xyz} \\[5pt] &= -x^2 y - xz^2 + x^2z - y^2z + xy^2 + yz^2 \end{align}$$
Now the gradient is
$$ \begin{align} \nabla f &= (-2xy - z^2 + 2xz + y^2, \\[5pt] &\phantom{000} -x^2 - 2yz + x + 2yz, \\[5pt] &\phantom{000} -2xz + x^2 - y^2 + 2yz) \end{align}$$
and
$$ \begin{align} \nabla f(1,1,1) &= (-2-1+2+1,\\[5pt] &-1-2+1+2, \\[5pt] &-2+1-1+2) \\[5pt] &= (0,0,0) \end{align}$$
Now the directional derivative in an unspecified direction, $\hat u = (u_1, u_2, u_3)$ is
$$ \begin{align} \nabla f(1,1,1) &\cdot (u_1, u_2, u_3) \\[5pt] &= (0,0,0) \cdot (u_1, u_2, u_3) = 0 \end{align}$$
So the directional derivative at this point in any direction is zero.
Notice that in this problem you have to be meticulous about your algebra — there are a lot of steps and many opportunities to make a sign error.
-
Suppose that $z = e^{xy+x-y}$.
- How fast is $z$ changing when we move away from the origin toward $(2, 1)$ ?
- In what direction should we move away from the origin for $z$ to change most rapidly? What would the maximum rate be?
Solution
Moving away from the origin toward $(2, 1)$ means moving in the direction of $\vec u = \langle 2, 1\rangle$. The unit vector is
$$\hat u = \frac{1}{\sqrt{5}}(2, 1)$$
The gradient of $f(x,y)$ is
$$ \begin{align} \nabla f &= \left( e^{xy+x-y}(y+1), e^{xy+x-y}(x-1) \right) \\[5pt] \nabla f(2,1) &= \left( e^{2+2-1}(1+1), e^{2+2-1}(1) \right) \\[5pt] &= (2e^3, e^3) \\[5pt] &= e^3(2, 1) \end{align}$$
Now
$$ \begin{align} \nabla f(2, 1) \cdot \hat u &= e^3(2, 1)\cdot (2, 1) \frac{1}{\sqrt{5}} \\[5pt] &= e^3[2(2)+1(1)] \frac{1}{\sqrt{5}} \\[5pt] &= e^3 \cdot 5 \sqrt{5} \end{align}$$
The direction of maximum slope is the gradient. The gradient we found above, evaluated at the origin is
$$ \begin{align} \nabla f &= \left( e^{xy+x-y}(y+1), e^{xy+x-y}(x-1) \right) \\[5pt] \nabla f(0,0) &= \left( e^0(0+1), e^0(0-1) \right) \\[5pt] &= (1, -1) \end{align}$$
That is the direction of steepest ascent. The magnitude of the slope is the length of this vector:
$$|(1, -1)| = \sqrt{2}$$
-
Consider the function $f(x,y) = \frac{x^2-y^2}{x^2+y^2}$. In what direction is the directional derivative of $f$ at $(1, 1)$ equal to zero?
Solution
We'll just call our unknown direction unit vector
$$\hat u = (u_1, u_2)$$
And we'll seek to find the $u_1$ and $u_2$ that yield
$$\nabla f \cdot \hat u = 0$$
Let's do the gradient in pieces:
$$ \begin{align} \frac{\partial f}{\partial x} &= \frac{(x^2+y^2)(2x) - (x^2-y^2)(2x)}{(x^2+y^2)^2} \\[5pt] &= \frac{\cancel{2x^3}+2xy^2 - \cancel{2x^3} + 2xy^2}{(x^2+y^2)^2} \\[5pt] &= \frac{4xy^2}{x^2+y^2)^2} \\[5pt] \frac{\partial f}{\partial y} &= \frac{(x^2+y^2)(-2y) - (x^2-y^2)(2y)}{(x^2+y^2)^2} \\[5pt] &= \frac{-2x^2y - \cancel{-2y^3} - 2x^2y + \cancel{2y^3}}{(x^2+y^2)^2} \\[5pt] &= \frac{-4xy^2}{(x^2+y^2)^2} \\[5pt] \rightarrow \nabla f &= \left( \frac{4xy^2}{x^2+y^2)^2}, \frac{-4xy^2}{(x^2+y^2)^2} \right) \end{align}$$
Evaluated at $(1, 1)$, the gradient is
$$\nabla f(1, 1) = \left( \frac{4}{2^2}, \frac{-4}{2^2} \right) = (1, -1)$$
Now in order to have a directional derivative of zero, we require that
$$ \begin{align} \nabla f(1, 1) \cdot (u_1, u_2) &= 0 \\[5pt] (1, -1) \cdot (u_1, u_2) &= 0 \\[5pt] u_1 - u^2 = 0 \end{align}$$
So the directional derivative is zero when $u_1 = u_2$, that is, directions specified by $(1, 1)$ and $(-1,-1)$.

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2024-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.