Specifying the direction of a vector
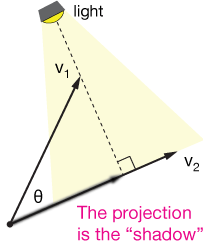
It's often necessary to figure out "how much" a vector points along a certain direction or directions. To do that, we use vector projections. The word projection hints at shadows cast on the wall or screen on which a projector light is shining. It's appropriate for vector projections. Here's a simple picture.

Vector $\vec{v_1}$ does not point purely in the direction of $\vec{v_2},$ but it does a little bit. Our projection vector is a measure of precisely how much of $\vec{v_1}$ points along $\vec{v_2}.$
Here's another way to visualize projections. think about a light or lamp pointing in a direction perpendicular to $\vec{v_2}.$
Then the "shadow" of $\vec{v_1}$ along $\vec{v_2}$ is its projection
In this section we'll learn how to calculate and use projections of one vector on another. We'll first do it using angles, then we'll repeat the process using only matrices. The angle &mdash/ in the dot product — is embedded in the matrix approach, but we'll never really need to calculate angles in that method. It's pretty cool.
Directions along axes
Sticking with three dimensions for now, it's fairly easy to find the angles that an $\mathbb{R}^3$ vector makes with the coordinate system. We identify the coordinate directions with the unit vectors $\hat{i} = (1, 0, 0), \; \hat{j} = (0, 1, 0),$ and $\hat{k} = (0, 0, 1).$ Now remember that the dot product of two vectors is
$$\vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}| \cos (\theta),$$
So that the cosine of the angle between them is
$$\cos(\theta) = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}.$$
Now if our vector of interest is $\vec{a}$ and $\vec{b}$ is the the unit vector $\hat{i})$ in the x direction, then that cosine is just
$$\cos(\theta) = \frac{\vec{a} \cdot \hat{i}}{|\vec{a}||\hat{i}|} = \frac{a_1}{|\vec{a}|},$$
where $a_1$ is the first (or $x$) coordinate of vector $\vec{a},$ selected by multiplying $\vec{a}$ by $(1, 0, 0)$, and the lengths of vectors $i,\; j,\; k$ (unit vectors) are one. So if we let the angles $\alpha$, $\beta$ and $\gamma$ be the angles between vector $\vec{a} = (a_1, a_2, a_3)$ and the three unit vectors that define our 3-D axis system, we obtain the three so-called direction cosines of that vector,
$$ \begin{align} \cos(\alpha) &= \frac{a_1}{|\vec{a}|} \\[5pt] \cos(\beta) &= \frac{a_2}{|\vec{a}|} \\[5pt] \cos(\gamma) &= \frac{a_3}{|\vec{a}|} \\[5pt] \end{align}$$
Now think about squaring each of those terms and adding them. We get
$$\frac{a_1^2}{|\vec{a}|^2} + \frac{a_2^2}{|\vec{a}|^2} + \frac{a_3^2}{|\vec{a}|^2} = \frac{a_1^2 + a_2^2 + a_3^2}{|a|^2}$$
Now notice that the numerator is just the length of $\vec{a}$ squared, as is the denominator, so this expression equals 1, which gives
$\cos^2(\alpha) + \cos^2(\beta) + \cos^2(\gamma) = 1,$ and
$$\frac{1}{|\vec{a}|} \vec{a} = (\cos(\alpha), \, \cos(\beta), \, \cos(\gamma)).$$
This is a nice compact formula for finding the direction cosines of any vector in $\mathbb{R}^3,$ and it can be generalized to any number of dimensions.
Here's a picture of those angles:

The angles are shown, and the green vectors are the projections of $\vec{a}$ on the coordinate axes. They are multiples of the unit vectors $\hat{i}, \, \hat{j}, \, \hat{k}.$
Example 1
Find the direction cosines of the $\mathbb{R}^3$ vector $\vec{a} = (1, \, 3, \, 4).$
$$ \begin{align} \cos(\alpha) &= \frac{1}{\sqrt{26}} \; \rightarrow \; \alpha = 79˚ \\[5pt] \cos(\beta) &= \frac{3}{\sqrt{26}} \; \rightarrow \; \beta = 54˚ \\[5pt] \cos(\gamma) &= \frac{4}{\sqrt{26}} \; \rightarrow \; \gamma = 38˚ \end{align}$$
Projections
Now let's move from direction angles to finding the projections of vectors on the coordinate axes to the projection of a vector on some other arbitrary vector. Here's the basic idea; we'd like to find the projection of vector b on vector a, where the points P, Q and R are endpoints of our vectors, as shown:

Notice from the figure that our projection, $\vec{s},$ is just the length of $\vec{b}$ multiplied by the cosine of the angle (the direction cosine). We'll use the dot product to find $\vec{s}.$
$$ \begin{align} \vec{a} \cdot \vec{b} &= |\vec{a}||\vec{b}| \cos(\theta) \\[5pt] &= |\vec{a}|(|\vec{b}| \cos(\theta)) \end{align}$$
Now the projection is just
$$ \begin{align} |\vec{b}| \cos(\theta) &= \frac{\vec{a} \cdot \vec{b}}{|\vec{a}|} \\[5pt] &= \frac{\vec{a}}{|\vec{a}|} \cdot \vec{b} \end{align}$$
So the projection of $\vec{b}$ along $\vec{a}$ is just dot product of the direction cosine vector, $(\vec{a}/| \vec{a}|),$ with $\vec{b}.$ Note that this is a scalar, which simply gives us the distance along $\vec{a}$ to the end of the projection vector.
Now if we want our result to be the full projection vector, we just need to multiply the the scalar projection by the normalized or unit a vector:
$$\frac{\vec{a}}{|\vec{a}|} \cdot \vec{b} \left( \frac{\vec{a}}{|\vec{a}|} \right) = (\vec{a} \cdot \vec{b}) \frac{\vec{a}}{|\vec{a}|^2}$$
These formulas can get a little confusing, but try to keep in mind the basic geometry of things. The length of the projection is just found using right-triangle trigonometry; to get the projection vector, just multiply this length by the unit vector in the direction of the vector your projecting onto (i.e. the normalized version of that vector).
Example 2
Determine the vector projection of $\vec{a} = (1, \, 2, \, 3)$ on $\vec{b} = (-3, \, 2, \, 1).$
$$ \begin{align} \frac{\vec{a}}{|\vec{a}|} \cdot \vec{b} &= \frac{1}{\sqrt{14}} [(1, 2, 3)\cdot (-3, 2, 1)] \\[5pt] &= \frac{4}{\sqrt{14}} \end{align}$$
Now to get the vector projection we just multiply that length by the unit vector a:
$$ \begin{align} \vec{s} &= \frac{4}{\sqrt{14}} \left[ \frac{1}{\sqrt{14}} (-3, 2, 1) \right] \\[5pt] &= \left( \frac{-6}{7}, \, \frac{4}{7}, \, \frac{2}{7} \right) \end{align}$$
Scalar & vector projections
The length of the projection (the scalar projection) of vector $\vec{b}$ on $\vec{a}$ is
$$s = \frac{\vec{a}}{|\vec{a}|} \cdot \vec{b}$$
The vector projection is that scalar value (scalar projection) multiplied by the unit or normalized vector $\vec{a}:$
$$\vec{s} = s \frac{\vec{a}}{|\vec{a}|}$$
Practice problems
-
Determine the direction cosines and the angles these $\mathbb{R}^3$ vectors form with the x, y and z axes.
- $\vec{a} = (-1, \, 0, \, 1)$
- $\vec{a} = (1, \, 2, \, -5)$
- $\vec{a} = (1, \, 2, \, 2)$
Solution
(a) Vector length:
$$|\vec{a}| = \sqrt{1 + 0 + 1} = \sqrt{2}$$
Cosines and angles:
$$ \begin{align} \cos(\alpha) &= \frac{a_1}{|\vec{a}|} = \frac{-1}{\sqrt{2}} \\[5pt] \alpha &= 45˚ \\[5pt] \cos(\beta) &= \frac{a_2}{|\vec{a}|} = \frac{0}{\sqrt{2}} \\[5pt] \beta &= 90˚ \\[5pt] \cos(\gamma) &= \frac{a_3}{|\vec{a}|} = \frac{1}{\sqrt{2}} \\[5pt] \gamma &= 45˚ \\[5pt] \end{align}$$
Recall that $\cos(x)$ is an even function, so $f(-x) = f(x)$
(b) Vector length:
$$|\vec{a}| = \sqrt{1 + 4 + 25} = \sqrt{30}$$
Cosines and angles:
$$ \begin{align} \cos(\alpha) &= \frac{1}{\sqrt{30}} \\[5pt] \alpha &= 79.5˚ \\[5pt] \cos(\beta) &= \frac{2}{\sqrt{30}} \\[5pt] \beta &= 43˚ \\[5pt] \cos(\gamma) &= \frac{-5}{\sqrt{30}} \\[5pt] \gamma &= 156˚ \\[5pt] \end{align}$$
(c) Vector length:
$$|\vec{a}| = \sqrt{1 + 4 + 4} = 3$$
Cosines and angles:
$$ \begin{align} \cos(\alpha) &= \frac{1}{3} \\[5pt] \alpha &= 70.5˚ \\[5pt] \cos(\beta) &= \frac{2}{3} \\[5pt] \beta &= 48˚ \\[5pt] \cos(\gamma) &= \frac{2}{3} \\[5pt] \gamma &= 48˚ \\[5pt] \end{align}$$
-
Calculate the scalar and vector projections of $\vec{b}$ onto $\vec{a}.$
- $\vec{a} = (-1, \, 2)$ $\vec{b} = (2, \, 3)$
- $\vec{a} = (-1, \, 2, \, 3)$ $\vec{b} = (1, \, 2, \, 4)$
- $\vec{a} = (2, \, 5, \, -2)$ $\vec{b} = (1, \, 1, \, 2)$
Solution
(a) Length of vector a:
$$|\vec{a}| = \sqrt{1 + 4} = \sqrt{5}$$
Scalar projection:
$$ \begin{align} s &= \frac{\vec{a}}{|\vec{a}|} \cdot b \\[5pt] &= \left( \frac{-1}{\sqrt{5}}, \frac{2}{\sqrt{5}} \right)\cdot (2, 3) \\[5pt] &= \frac{-2}{\sqrt{5}} + \frac{6}{\sqrt{5}} = \frac{4}{\sqrt{5}} \end{align}$$
Now the vector projection:
$$ \begin{align} \vec{s} &= s \frac{\vec{a}}{|\vec{a}|} \\[5pt] &= \frac{4}{\sqrt{5}} \left( \frac{-1}{\sqrt{5}}, \frac{2}{\sqrt{5}} \right) \\[5pt] &= \left( \frac{-4}{5}, \frac{8}{5} \right) \end{align}$$
(b) Length of vector a:
$$|\vec{a}| = \sqrt{1 + 4 + 9} = \sqrt{14}$$
Scalar projection:
$$ \begin{align} s &= \frac{\vec{a}}{|\vec{a}|} \cdot b \\[5pt] &= \left( \frac{-1}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}} \right)\cdot (1, 2, 4) \\[5pt] &= \frac{-1}{\sqrt{14}} + \frac{2}{\sqrt{14}} + \frac{12}{\sqrt{14}} \\[5pt] &= \frac{13}{\sqrt{14}} \end{align}$$
Now the vector projection:
$$ \begin{align} \vec{s} &= s \frac{\vec{a}}{|\vec{a}|} \\[5pt] &= \frac{13}{\sqrt{14}} \left( \frac{-1}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}} \right) \\[5pt] &= \left( \frac{-13}{14}, \frac{26}{14}, \frac{39}{14} \right) \\[5pt] &= \left( \frac{-13}{14}, \frac{13}{7}, \frac{39}{14} \right) \end{align}$$
(c) Length of vector a:
$$|\vec{a}| = \sqrt{4 + 25 + 4} = \sqrt{33}$$
Scalar projection:
$$ \begin{align} s &= \frac{\vec{a}}{|\vec{a}|} \cdot b \\[5pt] &= \left( \frac{2}{\sqrt{33}}, \frac{5}{\sqrt{33}}, \frac{-2}{\sqrt{33}} \right)\cdot (1, 1, 2) \\[5pt] &= \frac{2}{\sqrt{33}} + \frac{5}{\sqrt{33}} - \frac{2}{\sqrt{33}} \\[5pt] &= \frac{5}{\sqrt{33}} \end{align}$$
Now the vector projection:
$$ \begin{align} \vec{s} &= s \frac{\vec{a}}{|\vec{a}|} \\[5pt] &= \frac{5}{\sqrt{33}} \left( \frac{2}{\sqrt{33}}, \frac{5}{\sqrt{33}}, \frac{-2}{\sqrt{33}} \right) \\[5pt] &= \left( \frac{10}{33}, \frac{25}{33}, \frac{-10}{33} \right) \end{align}$$
-
Calculate the scalar projection of vector $\vec{b} = (1, 0, 1)$ on vector $\vec{a} = (1, 1, -1),$ and explain the result.
Solution
First calculate the length of $\vec{a}$:
$$|\vec{a}| = \sqrt{1 + 1 + 1} = \sqrt{3}$$
Now the scalar projection is
$$ \begin{align} \frac{\vec{a}}{|\vec{a}|} \cdot \vec{b} &= \left( \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{-1}{\sqrt{3}} \right) \cdot (1, 0, 1) \\[5pt] &= \frac{1}{\sqrt{3}} + 0 - \frac{1}{\sqrt{3}} = 0 \end{align}$$
The projection has a length of zero because vectors a and b are orthogonal. You can confirm this by calculating the dot product, which is zero. The "shadow" of vector b on vector a is a point, like the shadow of a pole in the noon-sun.
Matrix method
Let's do this partly by example. Here's the setup. We'd like to find the projection of vector $\vec b$ onto $\vec a$. One way to think of that is that we'd like to find vector $\vec p$, such that the distance between $\vec b$ and $\vec p$ (given by $\vec e$) is the shortest possible. That's like finding the distance from a point to a line — the line between them always forms a right angle to the line.

We define $\vec e$ as the difference between $\vec b$ and $\vec p$. It is $\vec e = \vec b - \vec p$. Now because $\vec e$ and $\vec p$ are perpendicular, we have
$$\vec e \cdot \vec p = 0$$
If we notice that the projection is just a piece of vector $\vec a$, namely $x \vec a$, where $x$ is a scalar, then we can write $\vec e = \vec b - x\vec a$, then we can write the dot product as $$(\vec b - x\vec a) \cdot \vec a$$
Writing that using a transposed vector (see dot products) gives
$$\vec a^T(\vec b - x \vec a) = 0$$
Then we can distribute multiplication on the left by $\vec a^T$ and simplify like this:
$$\begin{align} \vec a^T \vec b - x \vec a^T \vec a &= 0 \\[5pt] \vec a^T \vec b &= x \vec a^T \vec a \\[5pt] x &= \frac{\vec a^T \vec b}{\vec a^T \vec a} \end{align}$$
We said before that $\vec p = x \vec a$, which is the same as $\vec a x$, sow we have
$$\vec p = \vec a \; \frac{\vec a^T \vec b}{\vec a^T \vec a} \tag{1}$$
Before we go on to the last step, consider these two points:
- If $\vec b \; \longrightarrow \; 2 \vec b$, then the length of $\vec p$ is doubled: $\vec p \; \longrightarrow \; 2\vec p$. That makes sense. If the length of our vector $\vec b$ is doubled, then its projection along any other vector should double.
- If $\vec a \; \longrightarrow \; 2 \vec a$, then the length of $\vec p$ is unchanged because we end up with a 4 in both the numerator and denominator of our expression, and they cancel. That makes sense, too. The length of our projection shouldn't depend on the length of $\vec a$.
Now we just re-punctuate our expression (1) above in this way:
$$\vec p = \vec a \; \frac{\vec a^T \vec b}{\vec a^T \vec a} \longrightarrow \left( \frac{\color{magenta}{\vec a \vec a^T}}{\color{magenta}{\vec a^T \vec a}} \right) \; \vec b$$
This is just a matrix-vector multiplication. Let's define the projection matrix, the matrix in
$$P = \frac{\vec a \; \vec a^T}{\vec a^T \vec a}$$
This is a matrix because the denominator is a dot product – a scalar – and the numerator is a matrix. Now we have a handy projection matrix that will allow us to find projections without calculating angles — the angle is in there, but we just don't see it.
Projection matrix
To find the projection of $\vec b$ on a vector $\vec a$, we multiply $\vec b$ on the left by the projection matrix:
$$P = \frac{\vec a \; \vec a^T}{\vec a^T \vec a}$$
This works for vectors of any dimension, provided that the dimensions of $\vec a$ and $\vec b$ are the same.
Now let's apply this method to our example in the graph above. We have $\vec a$, so our projection matrix is
$$P = \frac{\vec a \; \vec a^T}{\vec a^T \vec a} = \frac{\left( \begin{matrix} 5 \\ 1 \end{matrix} \right) (5, \; 1)}{(5, \; 1) \left( \begin{matrix} 5 \\ 1 \end{matrix} \right)} = \frac{\left( \begin{matrix} 25 & 5 \\ 5 & 1 \end{matrix} \right)}{25 + 1}$$
Dividing through by the denominator, we get the transformation matrix:
$$P = \left( \begin{matrix} \frac{25}{26} & \frac{5}{26} \\ \frac{5}{26} & \frac{1}{26} \end{matrix} \right)$$
Now let's multiply our matrix $P$ by the vector $\vec b$ to get our projection:
$$\begin{align} P \vec b &= \left( \begin{matrix} \frac{25}{26} & \frac{5}{26} \\ \frac{5}{26} & \frac{1}{26} \end{matrix} \right) \left( \begin{matrix} 2 \\ 3 \end{matrix} \right) = \left( \begin{matrix} \frac{50}{26} + \frac{15}{26} \\ \frac{10}{26} + \frac{3}{26} \end{matrix} \right) \\[5pt] &= \left( \begin{matrix} \frac{65}{26} \\ \frac{13}{26} \end{matrix} \right) = \left( \begin{matrix} 2.5 \\ 0.5 \end{matrix} \right) \end{align}$$
A glance at the graph of all of our vectors above should assure you that this projection seems right. We can also check it by computing the dot product of our projection $\vec p$ with $\vec e = \vec b - \vec p$:
$$ \begin{align} \vec p^T \vec a &= (2.5, 0.5) \left( \begin{matrix} 2-2.5 \\ 3-0.5 \end{matrix} \right) \\[5pt] &= (2.5, 0.5) \left( \begin{matrix} -0.5 \\ 2.5 \end{matrix} \right) \\[5pt] &= -1.25 + 1.25 = 0 \end{align}$$
This method of finding projections scales perfectly for vectors of any size. We'll do a 3D example below.
Example 3
Find the projection of vector $\vec b = \left( \begin{matrix} 0 \\ -3 \\ 3 \end{matrix} \right)$ on the vector $\vec a = \left( \begin{matrix} 1 \\ 2 \\ 3 \end{matrix} \right)$.
$$\begin{align} P &= \frac{\vec a \; \vec a^T}{\vec a^T \; \vec a} = \frac{\left( \begin{matrix} 1 \\ 2 \\ 3 \end{matrix} \right) (1, 2, 3)}{(1, 2, 3) \left( \begin{matrix} 1 \\ 2 \\ 3 \end{matrix} \right)} \\[5pt] &= \frac{\left( \begin{matrix} 1 & 2 & 3 \\ 2 & 4 & 6 \\ 3 & 6 & 9 \end{matrix} \right)}{1 + 4 + 9} = \left( \begin{matrix} \frac{1}{14} & \frac{2}{14} & \frac{3}{14} \\ \frac{2}{14} & \frac{4}{14} & \frac{6}{14} \\ \frac{3}{14} & \frac{6}{14} & \frac{9}{14} \end{matrix} \right) \end{align}$$
Now we find the projection by multiplying our vector $\vec b$ on the left by the projection matrix:
$$P \vec b = \left( \begin{matrix} \frac{1}{14} & \frac{2}{14} & \frac{3}{14} \\ \frac{2}{14} & \frac{4}{14} & \frac{6}{14} \\ \frac{3}{14} & \frac{6}{14} & \frac{9}{14} \end{matrix} \right) \left( \begin{matrix} 0 \\ -3 \\ 3 \end{matrix} \right) = \left( \begin{matrix} \frac{3}{14} \\ \frac{6}{14} \\ \frac{9}{14} \end{matrix} \right)$$
In decimal form, our projection is
$$\vec p = \left( \begin{matrix} \frac{3}{14} \\ \frac{6}{14} \\ \frac{9}{14} \end{matrix} \right) = \left( \begin{matrix} 0.214 \\ 0.428 \\ 0.643 \end{matrix} \right)$$
Here's a 3D graph of all of these vectors. The red dashed line is the x-y-z path to vector $\vec a$, just to orient you as to how this axis system works.

Practice
Use the projection-matrix method to find the projections of vector $\vec a$ on $\vec b$ for each pair of vectors:
$$1. \phantom{00} \vec a = \left( \begin{matrix} -4 \\ -4 \end{matrix} \right) \phantom{000} \vec b = \left( \begin{matrix} 1 \\ 3 \end{matrix} \right)$$
$$2. \phantom{00} \vec a = \left( \begin{matrix} 1 \\ -2 \\ 3 \end{matrix} \right) \phantom{000} \vec b = \left( \begin{matrix} 1 \\ 0 \\ 4 \end{matrix} \right)$$
$$3. \phantom{00} \vec a = \left( \begin{matrix} 2 \\ -2 \\ 1 \\ 3 \end{matrix} \right) \phantom{000} \vec b = \left( \begin{matrix} 1 \\ 3 \\ 2 \\ -1 \end{matrix} \right)$$
Solutions
Wide equations: Scroll left ↔ right.
1. First calculate the projection matrix:
$$\frac{\vec a \vec a^T}{\vec a^T \vec a} = \frac{\left( \begin{matrix} -4 \\ -4 \end{matrix} \right)(-4, -4)}{(-4, -4) \left( \begin{matrix} -4 \\ -4 \end{matrix} \right)} = \frac{\left( \begin{matrix} 16 & 16 \\ 16 & 16 \end{matrix} \right)}{32} = \left( \begin{matrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{matrix} \right)$$
Now multiply $\vec b$ on the left to get the projection:
$$\left( \begin{matrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{matrix} \right) \left( \begin{matrix} 1 \\ 3 \end{matrix} \right) = \left( \begin{matrix} \frac{1}{2} + \frac{3}{2} \\ \frac{1}{2} + \frac{3}{2} \end{matrix} \right) = \left( \begin{matrix} 2 \\ 2 \end{matrix} \right)$$
2. First calculate the 3-D projection matrix:
$$\frac{\vec a \vec a^T}{\vec a^T \vec a} = \frac{\left( \begin{matrix} 1 \\ 2 \\ -3 \end{matrix} \right)(1, 2, -3)}{(1, 2, -3) \left( \begin{matrix} 1 \\ 2 \\ -3 \end{matrix} \right)} = \frac{\left( \begin{matrix} 1 & 2 & 3 \\ 2 & 4 & 6 \\ -3 & -6 & -9 \end{matrix} \right)}{14} = \left( \begin{matrix} \frac{1}{14} & \frac{2}{14} & \frac{3}{14} \\ \frac{2}{14} & \frac{4}{14} & \frac{6}{14} \\ \frac{-3}{14} & \frac{-6}{14} & \frac{-9}{14} \end{matrix} \right)$$
Now multiply $\vec b$ on the left to get the projection:
$$\left( \begin{matrix} \frac{1}{14} & \frac{2}{14} & \frac{3}{14} \\ \frac{2}{14} & \frac{4}{14} & \frac{6}{14} \\ \frac{-3}{14} & \frac{-6}{14} & \frac{-9}{14} \end{matrix} \right) \left( \begin{matrix} 1 \\ 0 \\ 4 \end{matrix} \right) = \left( \begin{matrix} \frac{1}{14} + \frac{12}{14} \\ \frac{2}{14} + \frac{24}{14} \\ \frac{-3}{14} - \frac{36}{14} \end{matrix} \right) = \left( \begin{matrix} \frac{13}{14} \\ \frac{26}{14} \\ -\frac{39}{14} \end{matrix} \right) = \left( \begin{matrix} 0.9285 \\ 1.857 \\ -2.786 \end{matrix} \right)$$

3. First calculate the 4-D projection matrix:
$$\frac{\vec a \vec a^T}{\vec a^T \vec a} = \frac{\left( \begin{matrix} 2 \\ -2 \\ 1 \\ 3 \end{matrix} \right)(2, -2, 1, 3)}{(2, -2, 1, 3) \left( \begin{matrix} 2 \\ -2 \\ 1 \\ 3 \end{matrix} \right)} = \frac{\left( \begin{matrix} 4 & -4 & 2 & 6 \\ -4 & 4 & -2 & -6 \\ 2 & -2 & 1 & 3 \\ 6 & -6 & 3 & 9 \end{matrix} \right)}{18} = \left( \begin{matrix} \frac{2}{9} & -\frac{2}{9} & \frac{1}{9} & \frac{1}{3} \\ -\frac{2}{9} & \frac{2}{9} & -\frac{1}{9} & -\frac{1}{3} \\ \frac{1}{9} & \frac{-1}{9} & \frac{1}{18} & \frac{1}{6} \\ \frac{1}{3} & -\frac{1}{3} & \frac{1}{6} & \frac{1}{2} \end{matrix} \right)$$
Now multiply $\vec b$ on the left to get the projection:
$$\left( \begin{matrix} \frac{2}{9} & -\frac{2}{9} & \frac{1}{9} & \frac{1}{3} \\ -\frac{2}{9} & \frac{2}{9} & -\frac{1}{9} & -\frac{1}{3} \\ \frac{1}{9} & \frac{-1}{9} & \frac{1}{18} & \frac{1}{6} \\ \frac{1}{3} & -\frac{1}{3} & \frac{1}{6} & \frac{1}{2} \end{matrix} \right) \left( \begin{matrix} 1 \\ 3 \\ 2 \\ -1 \end{matrix} \right) = \left( \begin{matrix} \frac{2}{9} - \frac{6}{9} + \frac{2}{9} - \frac{3}{9} \\ -\frac{2}{9} + \frac{6}{9} - \frac{2}{9} + \frac{3}{9} \\ \frac{1}{9} - \frac{3}{9} + \frac{1}{9} - \frac{1}{6} \\ \frac{1}{3} - 1 + \frac{1}{3} - \frac{1}{2}\end{matrix} \right) = \left( \begin{matrix} -\frac{5}{9} \\ \frac{5}{9} \\ -\frac{5}{24} \\ -\frac{5}{6} \end{matrix} \right)$$
Orthogonal
In two dimensions, orthogonal means perpendicular. But when we proceed to three or more dimensions, "perpendicular" isn't good enough. In 3-D a line and a plane can be perpendicular when viewed from one direction, but not perpendicular when viewed from an angle 90˚ away on the plane. The word orthogonal means perpendicular in every conceivable direction, no matter how many dimensions.

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.