Uses for double integrals
In this section we'll cover some important applications of multiple integrals (up to double integrals). They're useful for calculating quatities like
- Mass
- Moment of inertia
- Center of mass
- Probability density
- Expected values
where the properties of an object, such as density or temperature, vary over its volume. We'll take these one at a time and do some examples.
Density affects calculations of mass and moment of inertia; we'll cover those first.
Mass from density
When considering things like mass and moments of inertia of an object, we'll look back to solving for volumes of 3D objects by slicing. We'll refer to those slices as laminae (the plural of lamina). As a reminder, the density of an object is its mass divided by its volume. We usually use the Greek letter rho $( \; \rho \; )$ for density:
$$\rho = \frac{\text{mass}}{\text{volume}} = \frac{m}{V}.$$
For a lamina of uniform density, finding the mass and a few other properties is really just a matter of finding the volume of a stack of uniformly-dense slices and multiplying by some constant:

If we know a function that represents the varying density of a lamina and we know its 2D shape, we can find also find those properties because we can integrate over area as the density changes:
Take a look at a lamina divided into squares of area $dA$:
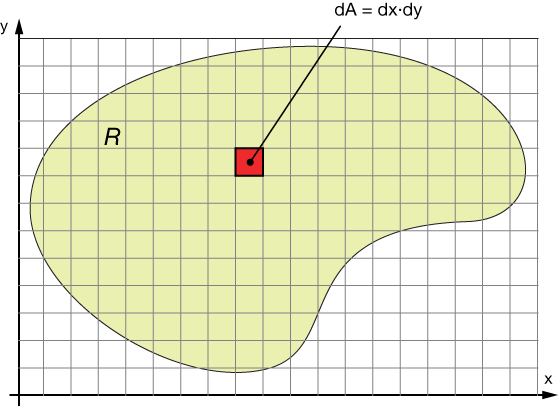
We can organize our squares with indices like a matrix: $R_{ij}$ represents the square in the $i^{th}$ row and $j^{th}$ column. The area of such a square is
$$ \begin{align} m &= \lim_{{k,l} \rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l \rho(x_{ij}^*, y_{ij}^*) \Delta A \tag{1} \\[5pt] &= \iint\limits_D \rho(x,y) \tag{2} \, dA \end{align}$$
In equation (1), we sum over the row and column indices $i$ and $j$, up to values ($k$ and $l$) that we can eventually take to infinity. The function $\rho(x_{ij}^*, y_{ij}^*)$ is a function of the points $x_{ij}^*$ and $y_{ij}^*$ that are guaranteed to be points of tangency to a tangent plane (or alternatively to tangent lines in the $x-$ and $y-$directions) by the mean value theorem. $\Delta A$ is the area of each element, which shrinks as we increase $k$ and $l$.
Equation (2) is the integral version that results from shrinking the area element $\Delta A$ to $dA$. The double integral is over the $x-$ and $y-$coordinates, in either order.
Mass
The mass of a 2D lamina with density function $\rho(x,y)$ is
$$\iint\limits_D \rho(x,y) \, dA$$
$$ \begin{align} m &= \int_0^5 dx \int_0^{5-x} dy = \int_0^5 dx \; y \; \bigg|_0^{5-x} \\[5pt] &= \int_0^5 dx \, (5-x) = 5x-\frac{x^2}{2} \bigg|_0^5 \\[5pt] &= 25-12.5=12.5 Kg \end{align}$$
Now with the density function, our integral is
$$ \begin{align} m &= \int_0^5 dx \int_0^{5-x} dy \,(xy) \\[5pt] &= \int_0^5 dx y \, \left(\frac{xy^2}{2}\right) \bigg|_0^{5-x} \\[5pt] &= \int_0^5 dx \, \frac{x(5-x)^2}{2} = \int_0^5 dx \, (x^3-10x^2+25x) \\[5pt] &= \left[ \frac{x^4}{4} - \frac{10x^3}{3} + \frac{25^2(6)}{2} \right]_0^5 \\[5pt] &= \frac{625(3)-1250(4)+25^2(6)}{12} = 26 \text{ Kg} \end{align}$$
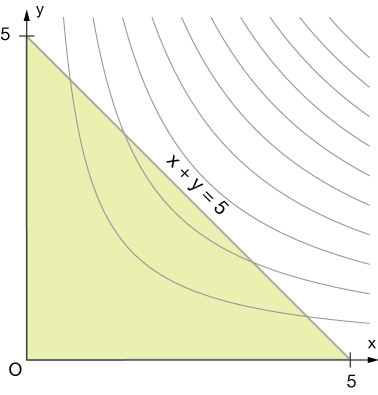
Here is a graph of our lamina with the contour plot of $f(x,y)=xy$ superimposed upon it. The gradient of the density function points down and to the left, so the lamina is more dense toward $(0,0)$.
Moment of inertia
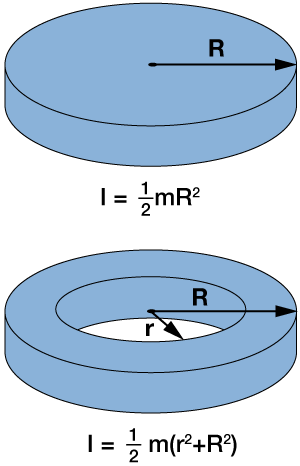
When an object is not rotating, we can simplify any equations of motion by concentrating (on paper) its mass at its center of mass. It's a helpful trick that's very often employed. When an object is rotating, however, everything depends on where the mass is located within it. Here are a couple of simple examples, a solid disk and a ring of the same mass rotating about their center of mass like a wheel-and-axle. These have different moments of inertia, thus when they're rotating they will have different angular momenta and other properties.
The moment of inertia of a disk is
$$I = \frac{1}{2} mR^2,$$
where $R$ is the radius and $m$ is the mass. The moment for ring of the same mass and same outer radius is
$$I = m(r^2 + R^2),$$
where $r$ is the inner radius — the radius of the hole. Now all of the mass is contained in the ring. The two moments are different.
Calculating moments of inertia
In general, the moment of inertia of $n$ point masses on a line (say $x$) is
$$I = \sum_{i=1}^n m_i x_i^2,$$
where $x$ is the distance of the mass from the origin of our coordinate system. If we divide a lamina into squares as we did above, we can consider each of these to be a point mass centered at $(x_{ij}^*, y_{ij}^*)$. Then we can sum up the 1D moments of inertia about the $x-$ and $y-$axes, respectively, like this:
$$ \begin{align} I_x &= \lim_{m,n \rightarrow \infty} \sum_{i=1}^m (y_{ij}^*)^2 \rho(x_{ij}^*, y_{ij}^*) \Delta A = \iint\limits_D y^2 \rho(x,y) \, dA \\[5pt] I_y &= \lim_{m,n \rightarrow \infty} \sum_{i=1}^m (x_{ij}^*)^2 \rho(x_{ij}^*, y_{ij}^*) \Delta A = \iint\limits_D x^2 \rho(x,y) \, dA \end{align}$$
Those are the moments about axes that lie in the plane of our disk, as shown. We can combine these to find the moment about the origin:
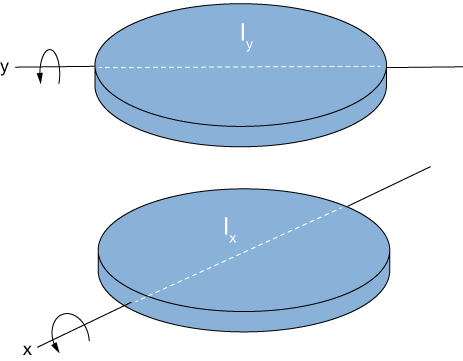
$$ \begin{align} I_O &= \lim_{m,n \rightarrow \infty} \sum_{i=1}^m \left[ (x_{ij}^*)^2 + (y_{ij}^*)^2\right] \rho(x_{ij}^*, y_{ij}^*) \Delta A \\[5pt] &= \iint\limits_D (x^2+y^2) \rho(x,y) \, dA \end{align}$$
The $D$ under the double integral sign just says the we're integrating over some 2D region, which we generally call $D$. When we actually do the integral, we'll have to define that more specifically.
Moment of inertia
The moments of inertia of a lamina rotating about an axis through the origin and contained by an axis traveling through it (the $x-$ and $y-$axes) are
$$\iint\limits_D x^2 \; \rho(x,y) \; dA \phantom{00} \text{and} \phantom{00} \iint\limits_D y^2 \; \rho(x,y) \; dA$$
The moment of inertia about the origin of a 2D lamina rotating about an axis orthogonal to the lamina, and with density function $\rho(x,y)$ is
$$\iint\limits_D (x^2+y^2) \; \rho(x,y) \; dA$$
Example 2
Now let's derive our two moment-of-inertia formulas of the blue disk and ring above using double integrals. We'll assume a constant density, $\rho$.
The disk
The moment of inertia of a disk of radius $R$ about the origin is
$$\iint_D (x^2+y^2)\rho \, dA$$
which we'll want to do in polar coordinates (don't forget the $r \, dr \, d\theta$):
$$ \begin{align} I_O &= \rho \int_0^{2\pi} d\theta \int_0^R de \, r^2 \, r \\[5pt] &= \rho \int_0^{2\pi} d\theta \, \left(\frac{r^4}{4}\right) \\[5pt] &= \rho \frac{r^4}{4} \theta \; \bigg|_0^{2\pi} \\[5pt] &= \frac{\pi \rho r^4}{2} \tag{1} \end{align}$$
Now let's recall that the mass is just the integral of the density over the same interval:
$$ \begin{align} I_O &= \rho \int_0^{2\pi} d\theta \int_0^R dr \, r \, \\[5pt] &= \rho \int_0^{2\pi} d\theta \, \left(\frac{r^2}{2}\right) \\[5pt] &= \rho \frac{r^2}{2} \theta \; \bigg|_0^{2\pi} \\[5pt] &= \pi \rho r^2 \tag{2} \end{align}$$
Substituting (2) into (2), we get the formula for the moment of inertia,
$$I_O = \frac{1}{2} mr^2$$.
The ring
Now let's derive the moment of inertia formula for the ring. The moment of inertia is
$$ \begin{align} I_O = \iint_D (x^2+y^2) \, \rho \, dA &= \rho \int_0^{2\pi} d\theta \int_r^R r^2 dr \, r^2 \, r \\[5pt] &= \rho \int_o^{2\pi} d\theta \frac{r^4}{4} \, \bigg|_r^R \\[5pt] &= \frac{\rho}{4} \int_0^{2\pi} R^4-r^4 \, d\theta \\[5pt] &= \frac{\pi \rho}{2} (R^4-r^4) \\[5pt] &= \frac{\pi \rho}{2} (R^2-r^2)^2 \end{align}$$
It's convenient here that $R^4-r^4$ is a difference of perfect squares, so $R^4-r^4 = (R^2-r^2)^2$. In a similar way as we did for the disk, we can write the mass of the ring as
$$m = \pi \rho (R^2 - r^2)$$
So the moment of inertia of the ring is
$$I_O = \frac{1}{2} m(R^2-r^2)$$
Center of mass
The center of mass of $n$ objects arranged in a line is
$$\text{com}=\frac{1}{M} \sum_{i=1}^n m_i r_i,$$
where
$$M = \sum_{i=1}^n m_i,$$
$m_i$ is the mass of the ith object and $r_i$ is its position in the line from some arbitrary point — say the origin.
For example, for the array of masses
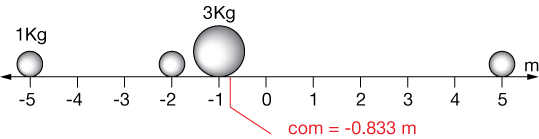
has center of mass
$$ \begin{align} \text{com}&=\frac{1}{6} [-5(1)-2(1)-1(3+5(1)] \\[5pt] &= -0.833 \; m \end{align}$$
The center of mass is the balance point (also called the center of balance) of the system of masses. The center of mass of the average human, for example, is roughly halfway through the body behind the navel.
For a 2D array of masses we just calculate the other coordinate of the com by performing the same sum in that coordinate, and so on for other dimensions.
The center of mass bears a strong relationship to the moment of inertia. We can relate them like this:
$$ \begin{align} x_{\text{com}} &= \frac{I_y}{m} = \frac{\iint\limits_D x \rho (x,y) \, dA}{\iint\limits_D \rho(x,y) \, dA} \\[5pt] y_{\text{com}} &= \frac{I_x}{m} = \frac{\iint\limits_D y \rho (x,y) \, dA}{\iint\limits_D \rho(x,y) \, dA} \end{align}$$
Example 3
Let's calculate the center of mass of our triangular area from Example 1 with the density function $\rho = xy$.
The mass of the lamina was calculated in Example 1. It's $m = 26.04 \, \text{Kg}$. The moment of inertia about the $y$ axis is
$$ \begin{align} I_y &= \iint\limits_D x \, \rho(x,y) \, dA = \int_0^5 dx \int_0^{5-x} dy \, (x^2y) \\[5pt] &= \frac{1}{2} \int_0^5 dx \, (x^2y^2) \bigg|_0^{5-x} \\[5pt] &= \frac{1}{2} \int_0^5 dx \, (x^4-10x^3+25x^2) \\[5pt] &= \frac{1}{2}\left[ x^2 \left( \frac{x^2}{5} - \frac{10x}{4} + \frac{25}{3} \right) \right]_0^5 \\[5pt] &= \frac{125}{2} \left( \frac{25}{5} - \frac{50}{4} + \frac{25}{3} \right) \\[5pt] &= \frac{125}{120} \cdot \frac{50}{60} = 0.8681 \, \text{Kg m} \end{align}$$
Now the center of mass in this direction is the ratio
$$x_{\text{com}} = \frac{I_y}{m} = \frac{0.8681 \text{Kg m}^2}{26.04 \text{ Kg}} = 0.0333 \text{ Kg}$$
Now by symmetry, $I_x = I_y$, and the mass is always the same, so the y-coordinate of the com will be the same. Thus the coordinates of the center of mass are $\text{com} = (0.0333, \; 0.0333)$. This makes sense because with this density function (see the graph in Example 1) most of the mass is concentrated very near the origin.
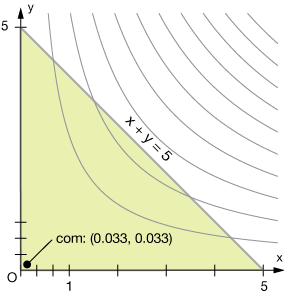
Recall that the center of mass of a lamina like this is called the centroid of the figure. If every human in the U.S. had the same mass and the continental U.S. was a lamina, then the population centroid of the U.S. today lies roughly in southern Missouri.
Probability
Another important application of integration over an area – via double integration – is calculating the total probability over an area given a probability density function, $P(x,y)$.
The basic idea is the same as for moment of inertia. The integral is
$$P = \iint\limits_D \, P(x,y) \; dA$$
The
The
Practice problems
Solve the following double integrals:
-
Find the volume of the function $f(x,y) = x+y$ over the region $R$, where $R$ is the region in the first quadrant of the $xy$ plane inside the circle $x^2+y^2 \le a^2$ and under the line $y = \sqrt{2} x$.
Solution
Here's the region over which we're integrating the function $f(x,y)=x+y$.

To do this integral in polar coordinates, we'll have to find the angle $\theta$ shown in the graph. That's just a matter of a little bit of trigonometry. The
red line is the line $y = \sqrt{2} x$, and the radius of the quarter-circle shown is $a$. The angle is then just:$$\theta = \tan^{-1} \left( \frac{y}{x} \right) = \tan^{-1} \left( \frac{\sqrt{2} x}{x} \right) = \sqrt{2}$$
So we have $\theta = \tan^{-1}(\sqrt{2}) = 0.955 \text{ rad}$ (about 54˚). So our limits of integration along $r$ will be $0$ to $a$ and along the $\theta$ coordinate they'll be $0$ to $0.955$. Now we need to convert the function $f(x,y)$ to $f(r,\theta)$. We just do a simple substitution, $x = r \, \cos(\theta)$ and $y = r \, \sin(\theta)$:
$$f(r, \theta) = r(\sin(\theta) + \cos(\theta))$$
Now our integral is
$$\int_0^{0.955} d\theta \int_0^a dr \; r^2(\sin(\theta) + \cos(\theta))$$
Now to solve the integral:
$$ \begin{align} \int_0^{0.955} & d\theta \int_0^a dr \; r^2(\sin(\theta) + \cos(\theta)) \\[5pt] &= \frac{r^3}{3} \bigg|_0^a \, \int_0^{0.955} d\theta \, (\sin(\theta) + \cos(\theta)) \\[5pt] &= \frac{a^3}{3} \int_0^{0.955} d\theta \, (\sin(\theta) + \cos(\theta)) \\[5pt] &= \frac{a^3}{3} \left[ -\cos{\theta} + \sin(\theta) \right]_0^{0.955} \\[5pt] &= \frac{a^3}{3} \left[ -\cos{0.955} + \sin(0.955) + \cos(0) - \sin(0) \right] \\[5pt] &= \frac{a^3}{3} \left[ -0.578 + 0.816 + 1 - 0 \right] \\[5pt] &= \frac{a^3}{3} \cdot 1.238 \\[5pt] &= 0.413 a^3 \end{align}$$
-
Calculate the volume inside of the sphere with equation $x^2 + y^2 + z^2 = 16$ and outside of the cylinder $x^2+y^2 = 4$.
Solution
Here is a picture of the volume we're interested in. It's the volume of the sphere of radius 4 minus what's inside the cylinder of radius 2:

The excluded area is the cylinder $x^2 + y^2 = 4$, which is $r = 2$ in polar coordinates (actually that equation is in cylindrical coordinates, which we'll tackle eventually. So we'll be integrating along the $r$ coordinate from $2$ to $4$, and in the $\theta$ coordinate all the way around the circle, from $0$ to $2 \pi$. The equation for the sphere transforms into polar coordinates using $r^2 = x^2 + y^2$ like this:
$$ \begin{align} x^2 + y^2 + z^2 &= 16 \\[5pt] z^2 &= 16 - x^2 - y^2 \\[5pt] z^2 &= 16 - (x^2 + y^2) \\[5pt] z^2 &= 16 - r^2 \\[5pt] z &= \sqrt{16-r^2} \end{align}$$
Now the integral setup is:
$$V = \int_0^{2 \pi} d \theta \int_2^4 dr \, r \, (16-r^2)^{\frac{1}{2}}$$
We can solve this integral by u-substitution:
$$ \begin{align} \text{Let } \; u &= 16-r^2 \phantom{00} \text{ then } \; du = -2r dr \\[5pt] \text{and } \; r &= 2 \rightarrow u = 12, \; r = 4 \rightarrow u = 0 \end{align}$$
Then our integral reduces to
$$ \require{cancel} \begin{align} V &= -\frac{1}{2} \int_0^{2 \pi} d \theta \int_{12}^0 u^{\frac{1}{2}} du \\[5pt] &= -\frac{1}{\cancel{2}}\frac{\cancel{2}}{3} \int_0^{2 \pi} d \theta \; u^{\frac{3}{2}} \bigg|_{12}^0 \\[5pt] &= -\frac{1}{3} \int_0^{2 \pi} d\theta \; \left[0-12^{\frac{3}{2}}\right] \\[5pt] &= \frac{1}{3} \cdot 24 \sqrt{3} \cdot \theta \bigg|_0^{2 \pi} \\[5pt] &= \frac{24 \sqrt{3}}{3} \cdot 2 \pi \\[5pt] &= 16 \pi \sqrt{3} \text{ units}^3 \end{align}$$
-
Calculate the volume that lies between the hyperboloid (two sheets) $-x^2-y^2+z^2 = 1$ and the plane $z = 2$.
Solution
Here's a plot of these two functions. The hyperboloid is of two sheets, and the plane $z = 2$ cuts through the top sheet, defining the volume outlined in yellow.

We need to find the intersection of these two figures. Inserting $z = 2$ into the equation of the hyperboloid gives
$$ \begin{align} -x^2 - y^2 + 2^2 &= 1 \\[5pt] -x^2 - y^2 &= -3 \\[5pt] x^2 + y^2 &= 3 \end{align}$$
This is the equation of a circle with radius $r = \sqrt{3}$, so our limits of integration along the $r$ coordinate will be $0 \rightarrow 3$. With respect to the $\theta$ coordinate, we'll integrate from $0$ to $2 \pi$.
Now the hyperboloid can be expressed in polar coordinates using $r^2 = x^2 + y^2$:
$$ \begin{align} -x^2 - y^2 + z^2 &= 1 \\[5pt] x^2 + y^2 &= 1 - z^2 \\[5pt] r^2 + 1 &= z^2 \\[5pt] z &= \pm \sqrt{r^2 + 1} \end{align}$$
So our volume double integral is
$$V = \int_0^{2\pi} d\theta \int_0^3 (r^2+1)^{\frac{1}{2}} \, r \, dr$$
We can solve this integral by u-substitution:
$$ \begin{align} \text{Let } \; u &= r^2+1 \phantom{00} \text{ then } \; du = 2r dr \\[5pt] \text{and } \; r &= 0 \rightarrow u = 1, \; r = \sqrt{3} \rightarrow u = 4 \end{align}$$
This reduced our integral to
$$ \begin{align} V &= \frac{1}{2} \int_0^{2\pi} d\theta \int_1^4 u^{\frac{1}{2}} \, r \, dr \\[5pt] &= \frac{1}{\cancel{2}} \frac{\cancel{2}}{3} \int_0^{2\pi} d\theta u^{\frac{3}{2}} \bigg|_1^4 \\[5pt] &= \frac{1}{3} \int_0^{2\pi} d\theta \, 4^{\frac{3}{2}} - 1 \\[5pt] &= \frac{7}{3} \int_0^{2\pi} d\theta \\[5pt] &= \frac{14 \pi}{3} \text{ units}^3 \end{align}$$
-
Convert the integral
$$\int_0^a \, dy \int_{-\sqrt{a^2-x^2}} \, dx \, [x^2y]$$
to polar coordinates, and find and interpret the resulting volume.
Solution
First we have to interpret the meaning of the limits of integration in the $x$ and $y$ coordinates and see if we can translate them to polar coordinates. The lower limit of integration in the $dx$ integral is $-\sqrt{a^2-y^2}$, which is the left side of a circle of radius $a$ in the $xy$-plane.
$$x^2+y^2=a^2 \; \rightarrow \; x = -\sqrt{a^2-y^2}$$

In polar coordinates our limits of integration will be $0$ to $a$ in the $r$ coordinate and either $\left[ \frac{\pi}{2}, -\frac{\pi}{2} \right]$ or $\left[ \frac{\pi}{2}, \frac{3\pi}{2} \right]$ in the $\theta$ coordinate. Conversion of the function $f(x,y) = x^2 y$ to polar coordinates gives
$$f(r, \theta) = r^3 \cos^2(\theta) \sin(\theta)$$
So our integral in polar coordinates is
$$V = \int_{\frac{\pi}{2}}^{\frac{\pi}{2}} d\theta \int_0^a dr \; r^4 \, \cos^2(\theta) \sin(\theta)$$
doing the inner integral yields
$$ \begin{align} V &= \int_{\frac{\pi}{2}}^{\frac{\pi}{2}} d\theta \int_0^a dr \; r^4 \, \cos^2(\theta) \sin(\theta) \\[5pt] &= \int_{\frac{\pi}{2}}^{\frac{\pi}{2}} d\theta \left[ \frac{r^5}{5} \right]_0^a \, \cos^2(\theta) \sin(\theta) \\[5pt] &= \frac{a^5}{5} \int_{\frac{\pi}{2}}^{\frac{\pi}{2}} d\theta \cos^2(\theta) \sin(\theta) \\[5pt] \end{align}$$
The $\theta$ part can be done by simple u-substitution:
$$ \begin{align} \text{Let } \; u &= \cos(\theta), \; \text{ then } \; du = \sin(\theta) d\theta \\[5pt] \theta &= \frac{\pi}{2} \; \rightarrow \; u = 0 \\[5pt] \theta &= \frac{3\pi}{2} \; \rightarrow \; u = 0 \end{align}$$
Making the substitutions and changing the limits of integration gives
$$V = \frac{a^5}{5} \int_0^0 du \, u^2$$
OK, now that's a weird result: The integral is zero when the limits are the same, so this volume must be zero. What's going on? Here are a couple of pictures of the function that will help.

Here is the function $f(x,y) = x^2y$. It has two-fold symmetry along the $x$ and $y$-axes around the origin.

If we look at this function from above and we draw our semicircular area of integration over it, we see that the upgoing (+) regions and donwgoing (-) regions are symmetric, so the volume has as much below as above the plane z=0, thus those positive and negative volumes cancel.
-
Use double integration in polar coordinates to calculate the area enclosed by the two cardioid $r = 1+\cos(\theta)$ and $r = 1-\cos(\theta)$.
Solution
Here are the two cardioids. The area enclosed by both is highlighted:


If we look just at the curve
$$r = 1-\cos(\theta),$$
we see that the region graphed between $\theta = -\frac{\pi}{2}$ and $\theta = \frac{\pi}{2}$ is half of the region of interest, so we can do the integral of that region and multiply by $2$.
Our integral and its solution are:
$$ \begin{align} A &= 2 \int_{\frac{-\pi}{2}}^{\frac{\pi}{2}} d\theta \int_0^{1-\cos(\theta)} \, dr \\[5pt] &= 2 \int_{\frac{-\pi}{2}}^{\frac{\pi}{2}} d\theta [r]_0^{1-\cos(\theta)} \\[5pt] &= 2 \int_{\frac{-\pi}{2}}^{\frac{\pi}{2}} d\theta [1-\cos(\theta)] \\[5pt] &= 2 \left[ \theta - \sin(\theta) \right]_{\frac{-\pi}{2}}^{\frac{\pi}{2}} \\[5pt] &= 2 \left[ \frac{\pi}{2} - 1 + \frac{\pi}{2} - 1 \right] \\[5pt] &= 2 \left[ \frac{\cancel{2} \pi}{\cancel{2}} - 2\right] \\[5pt] &= \frac{\pi}{2}-1 \text{ units}^2 \end{align}$$
lamina
The term lamina comes from anatomy. It means "layer" or "plate." In mathematics a lamina (plural = laminae) is usually an infinitessimally thin layer, as in calculus.
The Greek alphabet
| alpha | Α | α |
| beta | Β | β |
| gamma | Γ | γ |
| delta | Δ | δ |
| epsilon | Ε | ε |
| zeta | Ζ | ζ |
| eta | Η | η |
| theta | Θ | θ |
| iota | Ι | ι |
| kappa | Κ | κ |
| lambda | Λ | λ |
| mu | Μ | μ |
| nu | Ν | ν |
| xi | Ξ | ξ |
| omicron | Ο | ο |
| pi | Π | π |
| rho | Ρ | ρ |
| sigma | Σ | σ |
| tau | Τ | τ |
| upsilon | Υ | υ |
| phi | Φ | φ |
| chi | Χ | χ |
| psi | Ψ | ψ |
| omega | Ω | ω |

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2024-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.

