What is an electron?
I like to do an exercise with my chemistry students on the first day of class. I ask them to write down as many things as they know about an electron on a sheet of paper. Then we discuss them. All kinds of facts, some sophisticated, some not, come up:
Electrons are particles. They're waves. They're both particles and waves. They "orbit" the nuclei of atoms ( picture → ). They are very light. They "cause" electricity, and so on ...
Then I walk around the room with a recycling bin and ask them all to crumple up the papers and toss them in. We start over, and I tell them this:
Nothing in your life up to now has prepared you to understand what an electron really is. It's not your fault, you just don't live in the subatomic world. Neither do I. Electrons are what they are; they behave as they behave. They're not like baseballs and they're not like radio waves. Our job is not to interpret their behavior in terms of things we already know, but to come up with a mathematical model that fits the observed behavior and accept it.
Key Experiments
A few key experiments, performed around the turn of the 20th century, began to show that matter of or below the size of atoms exhibited behavior that contradicted what was known so far about the physical world — the world of baseballs and Newton's laws of motion. Although there were many such experiments, I'll just go over a few here that I think tell a compelling story.
Experiment 1: The Stern-Gerlach experiment
The Stern-Gerlach experiment is shown in the figure below. This is a very idealized version of the SG experiment. I've left out some experimental details, but rest assured that the essential experiment has been reproduced many thousands of times in various forms, all with the same result.

It works like this: Early on, physicists realized that electrons had magnetic properties because a beam of electrons could be deflected by placing a magnet nearby. The original televisions (cathode ray tubes) employed this principle.
It was also known that a spinning, charged object would exhibit magnetic properties, so the logical assumption was that electrons were spinning, charged particles – tiny little magnets with north and south poles.
Now in any group or ensemble of spinning charges, it would be reasonable to expect that all possible orientations of the magnetic field vector (the straight arrow pointing north in the figure) would be present. That is, we would expect those arrows to be randomly oriented in space. Because of this, we'd expect to find a whole range of differences in how one electron would interact with an external magnetic field compared to any other. Some would be strongly repelled or attracted to one pole, others would be more weakly affected. There would be a continuum of interactions on a scale from weak to strong.
So the expected result of the SG experiment was that a beam of electrons that passed through a magnetic field would be "smeared out" when they hit some detector screen, a reflection of the wide range of effects "felt" by the magnetic field of the electron. Here is the experiment. The expected result is shown in the top panel . . . and what really happened in the bottom:

What actually happens in the SG experiment is really stunning: The beam of electrons splits pretty cleanly into two separate beams, with nothing in the middle. These came to be called the "spin-up" and "spin-down" electrons (let's call these electrons +z and -z according to the coordinate system below).
Apparently, when it comes to "spin" (which I put in quotes because it's now understood not to be like the spin of a charged spinning baseball), electrons come in only two "orientations", with nothing in between.

Electron "spin"
Electrons exhibit only two kinds of "spin," which we'll label s, our first quantum number. It is customary to write these as s = ± ½.
s = ± ½ are called discrete spin "states" of an electron, and there are always only two, each with a value opposite the other.
Even stranger results ...
And there are some even stranger results from the S-G experiments. Consider the following three scenarios, illustrated in a kind of shorthand in the wide figure below. Each set of magnets has been replaced by a box to simplify the diagram. In the first scenario, we follow the original SG apparatus (the one above) by another set of magnets oriented in the same way, but we only capture one of the split beams, the +z, and we block the other. As we might expect, the beam is simply further deflected in the same direction - no big surprise there. We had previously "filtered" the beam, now we expect it to pass through another filter in the same way.
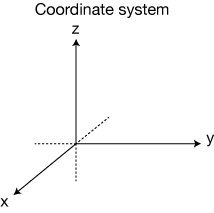
In the second experiment, we do the same thing, but this time we rotate the second set of magnets 90˚ around the electron-beam axis (the y-axis in the coordinate system above). The first experiment separated the beam into ±z components. This second experiment seeks to separate one of those beams (+z) into ±x beams. The result: This time the +z beam is split cleanly into two beams, +x and -x. Somehow there is, embedded inside the kind of spin along the z-direction, two kinds of spin along the x-direction.
Finally, we put a third set of SG magnets, acting in the z-direction, around one of the ±x beams from the previous experiment, blocking the other. The result: Two beams, ±z ! Apparently, upon going through the second set of magnets, all of the spin-up/spin-down (±z) identity of the beam was lost! Baseballs just don't behave like that. We clearly can't think of electrons as little "particles" just like shrunken baseballs.
Further SG experiments
... with odd results
Here's a second SG experiment. In the diagrams that follow, we'll simplify the diagram to block diagrams, and we'll call an SG apparatus that separates into plus and minus z-axis components SGz ... and we'll have SGx and SGy, too. This diagram contains two copies of our original SGz apparatus, which separates an electron beam into ±z components.
Not surprisingly, if we put the +z beam, selected from
the first SGz apparatus, through a second SGz apparatus, only the +z beam comes out, and with just the same intensity as when it entered. In other words, the beam was pre-filtered into +z electrons and they all went through as +z electrons.
The experiment works for the same kind of double selection of the -z beam just as well.

There appear to be sub-divisions of "spin"
Here, again is one copy of our original SGz apparatus, in green, followed by another that is rotated by 90˚, so that it exerts its magnetic separating force in the x-direction (see the axes definitions above).
Now what begins to happen here is somewhat unexpected. We thought that there were two versions of "spin," +z and -z, but now when the +z or -z electron beam is put through the SGx apparatus, we again see two beams, each with roughly the same number of electrons – i.e. the same intensity on a fluorescent screen.
So apparently, there is another classification to spin in addition to ±z, that we'll have to call ±x.
Except that the same thing happens if we use an SGy apparatus. So are there six different kinds of spin?
We know so far that if we take any electron beam that we don't know anything about and put it through an SG apparatus, it will be split into two beams, ±z, ±y or ±x, depending on which SG setup we use.
But if we already know that a beam contains only +z or -z or +x or ..., and we put it through a second identical SG apparatus, we get the result that we expect. A pure beam of known type does not separate further. OK.

It all falls apart ...
Here's a final experiment that establishes that electrons don't really behave the way we expect them to.
In this experiment, we'll use an SGz to separate a beam into ±z components, and we'll block the -z beam – we'll ignore it. We'll then do as we did in the last experiment, filter that +z beam into ±x beams. The we block the -x beam and pass the +x beam through another SGz apparatus.
Remember that we've already filtered out all of the -z electrons, but the result of this experiment is two beams of ±z character.
It seems like in doing the SGx filtering, we lost all information about the "z-ness" of the beam. The second SGz apparatus is "naive" to the ±z content of the beam and simply does its job, separating an electron beam into two components.

This was the confusing information that began a whole new way of thinking about electrons. The subject can get a little esoteric, but the result is that there are really only two versions of spin, and it's not really spin as we know it in our macroscopic world. It's just a characteristic of electrons to which we have to give a name, and spin stuck.
It turns out that every electron is both "spin up" and "spin down" all the time, until we "look," until we make a measurement. Then it "collapses" into one or the other state. Our goal here is not to understand this idea absolutely, just to accept that it's real, and that electrons have to have their own set of rules by which we understand them.
What we've learned
We have learned that one property of electrons, which for historical reasons we call "spin", is
We've also learned that spin is somehow affected by what kind of experiment or sorting was done before. When we pre-filter in one way, then filter in another, we lose all "memory" of the first filtering, strange behavior indeed.
Experiment 2: The Hydrogen-Atom Spectrum
Another piece of strange behavior observed at about the same time is the so-called "line spectrum" of the hydrogen atom. You are already familiar with the fact that a prism can be used to disperse (separate) the colors of white light (like light from the sun or a light bulb) into its component colors: Red, Orange, Yellow, Green, Blue, indigo and Violet (ROYGBIV). The rainbow that results from dispersion by a prism is called the spectrum of the sun.
We know that our sun is made up of many elements, everything, in fact, from hydrogen (H, most abundant) to Iron (Fe, 0.003% of all atoms in the sun). Although sunlight consists of more of some colors and less of others, we refer to its light as white light because it contains all colors visible to humans. However, if we look at the emission spectrum of only hot, glowing hydrogen gas (e.g. by putting H2 gas in a fluorescent bulb), dispersing it with a prism in just the same way, we see a completely different result (figure below).
Now instead of a rainbow, we see only four distinct "lines" or "bands" of colored light with nothing in between - thus the term "line spectrum."
The two spectra below show absorption by and emission from an ensemble of hydrogen atoms. In the top panel, we see that when white light is shined on a sample of hydrogen gas, the H absorbs certain discrete wavelengths of light, leaving the rest to pass through the prism and be dispersed into colors. The black bands represent missing light - light that has been absorbed by the hydrogen.
In the lower panel, Hydrogen gas has been excited with electricity in a kind of fluorescent tube, and passed through the prism. The light emanating from the excited hydrogen atoms consists of only four discrete color bands, red, cyan (light blue), blue and purple. The wavelengths of the colors are given (in nanometers), and form a characteristic fingerprint of hydrogen.
Indigo
What is indigo and why is it in the spectrum?
![]()
If you look at a rainbow in the sky or from a prism, it's pretty easy to pick out ROYGBV, but not the I for indigo, somewhere between blue and violet.
It turns out that it's there because Isaac Newton had certain occult views of his religion and strongly believed that the spectrum must have seven colors.

The actual emission spectrum of the sun (and anything else) is also really a line spectrum, but because there are so many different types of atoms in the sun, and because all have much more dense and complex line spectra than H (which is the simplest atom) they overlap and blur together to give our familiar rainbow. The color spectra of different stars are different because each star has a unique composition.
What does this mean? There is really only one explanation for the existence of line spectra.
Think about emission: In order to maintain the law of conservation of energy, if an electron in an atom is to "relax" from a state of higher kinetic energy (the energy of motion) to a lower one, it must get rid of that energy somehow. It does so by radiating that energy away, usually in the form of one particular color of visible light. If the electrons in an atom could have any kinetic energy at all, we would expect a continuous spectrum - a rainbow. That we see a discrete spectrum (one made up of only specific colors of light) is evidence that electrons can't just have any energy. They can only take on discrete energies, with nothing in between.
Energy Levels of Hydrogen
The diagram below explains the H-atom emission spectrum. It contains a bit more information than you need right now,
but just concentrate on the middle set of arrows that goes with the visible emission spectrum (hydrogen also has emission lines in the invisible infrared and ultraviolet regions of the spectrum).
We assume that electricity excites the electron in a H atom to one of the "excited states" - higher energy levels than the ground state or lowest energy level.
When those excited electrons relax, they emit light that exactly equals the difference between the two energy levels that define the transition.
This must be so because energy must be conserved — neither created out of nothing, nor destroyed. You can see that the visible line spectrum represents transitions from excited states to the second-highest energy level. The spectra of larger atoms are proportionally more complicated.
The absorption spectrum is just the reverse. The electron in a ground-state hydrogen atom absorbs certain energies of light in order to achieve an excited state.
The idea that the energies of electrons in atoms are discrete and not continuous is another example of the non-classical (not like objects we're used to seeing) and unexpected behavior of electrons that begged for a non-classical explanation.

Baseballs vs. electrons

Experiment 3: The Photoelectric Effect
One last experiment will shed some more light on the behavior of electrons. The photoelectric effect is illustrated below. When certain metals are irradiated with light, electrons, which we presume to be bound to the atoms of the metal, are ejected from the surface and can be collected, run through a wire and measured as an electric current.

When researchers were able to vary the energy of the incoming light beam, they got a surprising result. When the frequency (proportional to the energy of the light) was low enough, nothing at all happened to the metal. However, once a certain threshold was reached, electrons previously bound to the metal atoms were ejected. They became free electrons.
Moreover, after the threshold was reached, the ejected electrons left the metal with higher kinetic energies (speeds) in proportion to the increase in frequency. This graph illustrates this idea.

It also didn't matter if the light was brighter – meaning more photons striking the metal per unit time, the effect was the same of the energy of each photon was below the threshold – no effect.
The conclusion of the photoelectric effect experiments was that there was some threshold energy that had to be met before an electron could be pried away from its atom. After that, it behaved as a "free" electron, able to take on any value of kinetic energy at all — like a baseball.
Electrons bound to atoms do not act like free electrons. Free electrons act more like (a little more like) classical particles than bound electrons.
What do all of these experiments mean?
After the turn of the 20th century, all of these experiments were leading a few scientists toward a model of the simplest atom, hydrogen. I won't go through all of the early attempts here. They are covered elsewhere. Suffice to say that they all had at least one flaw, and any useful theory has to predict all properties accurately. Early attempts came close to reproducing the observed energy levels, but didn't get them exactly, and some failed to predict other properties of hydrogen that had been measured.
In about 1926, Erwin Schrödinger, an Austrian physicist known for his work on wave equations, took a look at the models and noted that they looked a lot like his wave equations. He published a series of papers that showed how a wave equation could fit the data perfectly, and correctly predict many other phenomena that had been puzzling researchers. Schrödinger's equation is beyond the scope of the mathematical background you likely have. It is a differential equation that requires calculus and a few other tricks to solve. Here it is (don't panic!):
DON'T PANIC ... Below you'll find a few equations that might blow your mind. Don't worry, you're not meant to understand them as a newcomer to chemistry. In fact, it takes a few years to learn all of the math you'd need to derive them. I only show them to you so that you'll know that there's a mathematical basis for the strange orbital shapes to come.
Schrödinger's equation is not likely the kind of equation you've seen before. The Hamiltonian operator [the thing in brackets] "operates" (does some mathematical things) to a "wave function" that represents the electron in the H-atom, and returns to us the energy levels multiplied by the same wave function. Resist the temptation just to cancel $\psi(x)$ from both sides — it's not that kind of equation ($\psi$ is the Greek letter "psi", pronounced like "sigh").
The Schrödinger equation
$$\left[ \frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} + V(x) \right] \psi(x) = E \psi (x)$$
- The expression in [square brackets] is called the Hamiltonian operator.
- $\psi(x)$ is the wave function.
- $E$ is the energy of that particular wave function.
What's important about this equation is that it is solved not by numbers, but by functions (the $\psi(x)$). In particular, this equation is solved by a set of 3-dimensional functions called spherical harmonics, which represent, in some sense, the "location" of the electron in the H-atom. Location is in quotes because the electron behaves more like a wave when bound to the atom, so its location is ill-defined.
(The more advanced reader will note that I've written the 1-dimensional Schrödinger equation above, but you get the idea).
Here is the equation for the spherical harmonics. Again, don't panic. There's a lot here to understand, and we only have the mathematical background to scratch the surface.
The Spherical Harmonics
$$Y_l^m (\theta, \, \phi) = N e^{im \phi} P_l^m (cos(\theta))$$
$l$ and $m$ are integer indices, with $l = 0, 1, 2, \dots$ and $m = -1, -2+1, \dots, i-2, i-1, i$
The important thing to note about the spherical harmonics is that
(1) They contain a trigonometric function (cosine, in this case), but in three dimensions. That gives them the shapes you will see below.
(2) They are indexed by the indices $L$ and $m$. (Note: I am using a capital $L$ in this text, but we generally write a lower-case script L ... it just looks like a one in this font.) In the mathematical world of the spherical harmonics, these are just counting or index variables that make sure we write the functions correctly and in the right order. But in the subatomic world, they become two of our four quantum numbers of any electron.
The quantum numbers describe all of the relevant characteristics of any electron, and they arise from the fact that the energies of electrons are not continuous, but quantized, as we learned from our key experiments. Schrödinger's equation accurately predicts all of the properties of the Hydrogen atom.
Quantum Numbers
This initial discussion of quantum numbers isn't going to go down very well. It's very foreign to think of things this way. It will seem made-up and artificial. Rest assured that quantum numbers are a direct result of the kinds of solutions that come out of the Schrödinger equation. Work through it. By the time we're done, it will make better sense.
The first quantum number, the principal quantum number, is called $n$. It labels the energy level of an electron. In the H-atom energy level diagram above, you can see that the levels are labeled from lowest to highest, starting at $n=1$. We usually say that $n$ labels which shell that the electron occupies. Inner shells are small and closer to the nucleus, and outer shells are larger. Inner shells are of lower energy, outer shells of higher energy.
The second quantum number is $L$, the azimuthal quantum number. It describes the general shape of the orbital occupied (created, actually) by an electron.
The shape comes from the 3-D shape of the spherical harmonic functions. $L$ runs from $0$ to $n-1$, so for $n = 1$, $L$ can only be zero, but for $n = 2$, $L = 0$ or $1$, and so on.
It is an artifact of the development of the quantum theory that we call $L=0$ orbitals $s$-orbitals, and for $L=1,2,3$ we call them $p$, $d$ and $f$, respectively. $p$, $d$ and $f$ orbitals are composed of several sub-orbitals. These rules seem strange, but trust me, they pop right out of the mathematics.
The third quantum number is $m_L$, the magnetic quantum number. It labels the sub-orbitals within a $p, \; d$ or $f$ orbital. The values of $m$ depend on $L$. If $L = 0$, then $m = 0$; if $L = 1$, then $m_L = -1, \; 0, \; 1$; if $L = 2$, then $m_L = -2, \; -1, \; 0, \; 1, \; 2$; and so on, or $m_L = -L, \; -L+1, \; \dots , L-1, \; L$.
The final quantum number is the spin quantum number, which we have met before in the SG experiments. It is usually called $m_s$, and takes on the values $\pm \frac{1}{2}$. In the world of subatomic particles, there are particles with "half-integer spin" (Fermions) like ½, 3/2, and with "integer spin" (Bosons), like 1, 2, ... Electrons are Fermions.
Below is a chart of the $s, \; p$, and $d$ orbital shapes.

The shapes of the orbitals
The lowest-energy orbital, with $L=0$, is called an $s$-orbital. Its shape is always a sphere, as shown on the right.
In the spherical harmonic functions that describe the spaces that electrons occupy, when the quantum number $L$ is zero, the quantum number $m_L$ must also be zero, and the only possible 3-D shape that can arise is the sphere. There are no sub-orbitals of an $s$-orbital
We interpret this sphere as the region within which it's most likely to find an electron if we could find it. Remember that an electron bound to an atom is acting much more like a wave than a tiny particle.
Every shell (labeled by $n$) has one s-orbital, each larger than the one below it.
Each $s$-orbital can hold, at most, two electrons, and those must have paired spins, one $+ \frac{1}{2}$, the other $-\frac{1}{2}$. It's another quirk of quantum behavior that we just have to get used to: No two electrons bound to an atom can have exactly the same set of quantum numbers, $n, \; L, \; m_L$ and $m_s$.

The Pauli exclusion principle
No two electrons in an atom can have the same set of quantum numbers, $n$, $L$, $m_L$ and $m_s$.
p-Orbitals

$P$-orbitals are where things start getting interesting. How on Earth does this strange dumbbell shape arise?
We have to remember where we began. Electrons must be understood on their own terms. These orbital shapes arise from the solutions to the Schrödinger equation which exactly reproduce all that is known about the H-atom. They are what they are.
P-orbitals actually resemble some of the kinds of patterns you might observe if you could see electromagnetic waves coming off of an antenna. The p-orbitals look like this because electrons act more like waves than particles when they're bound to atoms. One of the ways waves interact is to interfere with one another, and that interference can lead to "nodes" like the pinched-off area in the middle of this p-orbital.
There are three p sub-orbitals, only one of which, the $p_z$ orbital, is drawn above. There are also p-orbitals that lie along the $x$- and $y$-axes, $p_x$ and $p_y$. The point is not really that they lie along these axes specifically, but that they exist at 90˚ angles to one another in 3 dimensions (another way to say this is that they're orthogonal). This has been verified in many experiments.
In an atom, each $p$ sub-orbital can hold two electrons, as long as their spins are different.
For example, two electrons in the $p_y$ orbital of the second energy level ($n = 2$) of an atom would have the quantum numbers $n, \; L, \; m_L, \; m_s = 2, 1, 1$ (or 0 or -1 – we don't often specify which mL quantum number goes with which orbital), ±½ - unique sets of quantum numbers. Each $p$-orbital (including all three sub-orbitals) can hold six electrons. For each value of the quantum number $n \gt 1$, there is a $p$-orbital (which consists of three sub-orbitals), which can hold six electrons.
It's getting weird(er): $d$-orbitals
D-orbitals ($L = 2$) are composed of five different types of sub-orbitals, labeled by $m_L = -2, \; -1, \; 0 \; 1, \; 2$.
While the shapes of many of the $d$ sub-orbitals are reminiscent of the $p$-orbitals, they are different. One, the $d_{z2}$ orbital is bizarre indeed, containing one toroidal (donut-shaped) region. Nevertheless, these orbitals represent the regions in which an electron with the energy of a $d$-orbital are most likely to be found.
Because $L = 0, \; 1, \dots n-1$, the lowest shell (quantum number $n$) to even have $d$ orbitals is $n = 3$. The $n= 3$ shell contains $s, \; p$ and $d$ orbitals.
D-orbitals are what give metals their character. We'll get to that another time.
The $d$ sub-orbitals are given names, analogous to $p_x, \; p_y$ and $p_z$, of $d_{xy}, \; d_{xz}\; , d_{yz}$, $d_{x2-y2}$, and $d_z^2$.
Each sub-orbital of a $d$-orbital can hold two spin-paired electrons, for a total of ten electrons in any $d$-orbital.
The table below summarizes the possible values of each of the quantum numbers.


What we've learned so far is that the mere presence of electrons in an atom (bound by attraction to the nucleus) creates a situation in which electrons behave like three-dimensional waves. They interfere with one another in the way that waves do,
and they occupy strangely-shaped regions of space modeled by functions called spherical harmonics. Which of these shapes (orbitals) the electron in an H-atom occupies depends on its total energy.
In the next section, see how electrons fit into bigger atoms...

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.