The shape of molecules
What do molecules look like? What is their three-dimensional shape, and how might we predict it? VSEPR* is a model that is pretty good at predicting the general features, if not the details, of the structures of polyatomic molecules.
The basic idea is that when bonds form, they create a region of relatively high electron density – places where the electrons "spend most of their time." That's really what bonds are: Localized regions where the electron density is high between atoms sharing electrons.
All of that concentrated negative charge in a bond tends to repel any other such region that comes close to it. The result is that bonds around a central atom tend to arrange themselves so as to be as far away from each other as possible, but still connected.
The best way to learn this is through examples, so let's take a look at a few.
VSEPR is sometimes called "vesper," even though it's not phonetic. Use vesper if you'd like.
Covalent bonds
Bonds in molecules are regions of high electron density, and thus high negative charge. When a central atom is bound to several other atoms, the bonds (bonding orbitals) tend to repel one another, moving as far apart as possible.
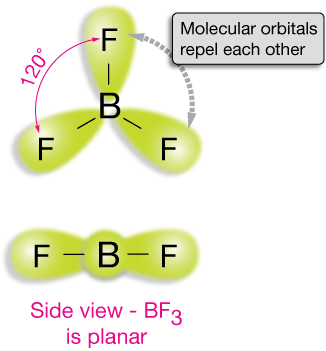
Boron trifluoride, BF3
In BF3, the boron atom brings three valence electrons, and each fluorine has 7, so each atom will have a perfect octet of electrons if three single bonds are formed.
The bonding orbitals that result from the sharing of two electrons between each pair of atoms look something like the yellow (p-orbital-like) lobe in the drawing. Because their charges are identical, they repel one another.
The resulting geometry is the trigonal-planar (triangle-shaped, flat) one shown, with all bond angles (the F-B-F angles) at 120˚. With the geometry of BF3 in mind, what might you predict about the shapes of BCl3 and BH3 ?
That's basically how VSEPR works: The electrons of the bonds repel one another, moving "arms" of the structure as far apart as possible.
Carbon dioxide, CO2
In the CO2 molecule, each oxygen is double bonded to the central carbon, as the Lewis structure on the left shows. VSEPR predicts that the molecule will be linear because that's the configuration that moves the C=O bonds as far apart as possible.

The actual picture is really more like that shown on the right, because each oxygen atom has two lone electron pairs.
Notice that even these lone pairs, which don't really contribute to what we think of as the structure of the molecule, orient in such a way as to maximize the distance between them. Notice the similarity between the left-most two lone pairs and the C atom, and the shape of BF3.

Generally, when we speak of the structure of a molecule, we're talking about the location of the nuclei of atoms, but we even have to be careful there for two reasons: (1) All atoms move all of the time, so we're always talking about average positions of atoms as they vibrate, and (2) those lone pairs can be big factors in determining the shape and properties of a molecule, as we'll see in the next example ...
Water (H2O)
Water bonds with two single bonds, as shown in the Lewis structure below, leaving two lone pairs of electrons in p-like orbitals (they're actually hybrid orbitals, mixing s and p orbitals). That leaves four regions of high electron density, all of which move as far from each of the others as possible.

The result is the structure shown above. The catch is that those four electron-rich regions aren't all equal. The two O-H bonds are identical, and the two lone pairs are identical, but the two pairs are different. The result is that in water, the picture (which actually looks more like the one below), is not exactly what we'd expect. The model on the right (above) uses a kind of notation often used to show 3-D structure in molecules. The solid wedge is meant to show that the H atom pokes out of the plane of the screen, and the dashed one shows that its H is angled back behind the plane.

In water the H-O-H angle is about 104.5˚. In a molecule with a central atom and four equal "arms," we'd expect to find the perfect tetrahedral angle of 109.5˚. But in water, the lone pairs actually push the two hydrogen atoms a little closer together than that, into the lowest-energy configuration for water.
Here is what I mean by tetrahedral. A regular tetrahedron is formed by joining the edges of four equilateral triangles. In the case of water, the oxygen would be located in the center, and the oxygens and lone pairs at vertices as shown. The water tetrahedron is just a little bit distorted because the O-H bonds and lone pairs aren't exactly equal.

Methane (CH4)
Here's an example of a perfect tetrahedral arrangement. Each C-H bond in methane is identical to the other, so we expect them to move as far apart as possible, which means to the perfect tetrahedral angle of 109.5˚. The Lewis structure looks like this:

and the tetrahedral structure can be represented in a number of ways; here are two:

Don't forget the main idea of VSEPR here: Electrons, whether in lone pairs or in bonds, need to move as far apart as possible because of electrostatic repulsion. That leads to certain geometries, depending on how things are bonded. Our task is just to understand the look of some of those geometries, and rationalize why they form.
Sulfur hexafluoride (SF6)
Now let's add more atoms around a central atom. Look at the Lewis structure of SF6. It's one of those exceptions to the octet rule, where the d-orbitals of the central sulfur can rearrange to let it have ten valence electrons:

The arrangement that maximizes the distance between all of the fluorines is called an octahedral or square bipyramidal structure. Again, it's not that the octahedral structure is something that nature aims for, it's just that it happens to be the structure in which all of the vertices (where the F-atoms are) are as far apart as possible, yet the same distance from the center (where the sulfur is). There are other such bipyramidal structures, summed up in the table below.
A table of VSEPR geometries
Now we might be able to extend these examples to some general rules. The table below might help you think it through, and if you're working problems, you can download it as a .pdf file.
Notice that when a lone pair is present, the measured value of certain bond angles is generally larger than expected.
For example, look at the column in the table for compounds with one lone pair of electrons. For BF3 (one of our examples above), the bond angles were 120˚, or exactly 1/3 of 360˚. But when one of the fluorines is replaced by a lone pair (top box in that column), the bond angle expands, essentially because the lone pair is a little smaller and a little less repulsive than a bond, and allows that expansion. See if you can apply this same rationale to other cases in the table.
Example 1

Now the central tin atom is surrounded by four regions of electron density.
Three are equivalent single bonds to Cl atoms, and the fourth is a lone pair. We might, therefore, expect a structure like this:

If all four regions were equivalent, we'd expect a 109.5˚ angle between each, but they are different. The lone pair is smaller than the bonds and their chlorine atoms, so the "tripod" can spread out a bit to relieve some repulsive strain.
Example 2

The central iodine atom is surrounded by 5 chlorines and a lone pair, so this structure seems reasonable by VSEPR:

In the actual structure, the four chlorines arranged on the square base of this (upside-down) square pyramid would move closer to the lone pair than shown. The lone pair just takes up less space, relieving some of the repulsive strain between the chlorines.
Example 3
Consider one possible bonding arrangement of NO2-, with single N–O bonds. The formal charges on the nitrogen and the two (equivalent) oxygens are shown. Recall that formal charge is (number of valence electrons) - (number of bonds) - (number of electrons in lone pairs).
![]()
Because there are two oxygens, our negative charge is accounted for here. This structure has two problems. First, N only has 6 valence electrons, and second, the formal charges might be reduced in another arrangement. Here is one that does the trick:

In the single-double N–O arrangement, N has eight electrons, and the formal charges are lower, while still producing our overall -1 charge. The optimal structure is a resonance between these two structures

which yields an overall structure that looks like this. The bond angle, 115˚, slightly smaller than the trigonal-planar angle of 120˚, has been measured in the laboratory.

ClO2-
The story is very similar for ClO2--. Here is one structure, in which all valences are satisfied,
![]()
but this structure, in which Cl has ten valence electrons, has lower formal charges:

It implies another resonance structure, this time with two lone electron pairs on the central atom:
![]()
The structure is another bent molecule, but this time the angle is a bit wider, due to the presence of two lone pairs instead of one.

Example 4

The formal charges on the chlorine atom and the two types of oxygen atoms are found by subtracting the number of bonds and the number or electrons in lone pairs from the number of valence electrons of each atom:

The sum of these charges gives the ionic charge of -1. Here is another Lewis structure. This one surrounds Cl with 12 electrons.

The formal charges still yield the -1 overall charge ,but they are smaller, so this is more likely to be the correct arrangement of bonds in ClO3-.

This arrangement really represents a resonance structure,

in which each equivalent bond has a character between single and double, like this.

We expect the bond angles to roughly equal the tetrahedral angle, but probably a bit larger given that the lone pair of electrons on the chlorine would take up less space than a fourth oxygen.
Practice problems
For each of the following molecules and ions: (1) draw a Lewis structure, (2) Make sure the sum of its formal charges is correct and represents the structure with the least absolute sum of formal charges, and (3) sketch the structure that VSEPR theory predicts.
-
HCN
Solution

-
ClF4+
Solution

-
CH2Cl2
Solution

-
OF2
Solution

-
IF6+
Solution

-
MnO4-
Solution

-
SF5-
Solution

-
NI3
Solution

-
I3+
Solution

-
XeO3
Solution


![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2016-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.
