Acids and bases are key components of many chemical reactions and systems. To know chemistry, one must know acid-base chemistry — and the two always go together.
Any chemical substance can either be acidic (strongly or weakly), neutral, or basic (strongly or weakly). Here are a few examples of acids, bases and neutral compounds along a continuum, from strong acid to strong base.

We will encounter other, more subtle definitions of acids and bases later, but for now, a good working definition that is useful most of the time is:
Acids are H+ (proton) donors
Bases are OH- (hydroxyl ion) donors
Acids are substances that either directly or indirectly raise the concentration of H+ ions (protons) in solution. Bases either directly or indirectly raise the concentration of OH- (hydroxyl ions) in solution.
You will want to memorize the strongest acids and bases (table below).
Strong acids and bases are those which are completely soluble in water.
HCl, HBr, HI – the halogenic acids
H2SO4 – sulfuric acid
HNO3 – nitric acid
HClO4 – perchloric acid
KOH – potassium hydroxide
NaOH – sodium hydroxide
Ba(OH)2 – barium hydroxide
Ca(OH)2 – calcium hydroxide
In the sense of acids and bases, "strong" means that the compound completely dissociates in water. Weak acids and bases only dissociate partly, or are insoluble.
HCl, hydrochloric acid*, is a strong acid—one of the strongest. It dissociates completely into a chloride ion and a free proton (from here on, I'll call a +1 hydrogen ion a proton, because that's what it is).
It's the free proton that makes a strong acid different from a neutral compound. If one mole of HCl is dissolved into one liter of water, the concentration of H+ will be 1M because HCl dissociates completely (it is a strong electrolyte - that's the reason for the single arrow in the dissociation equation). The same is true of the other acids on the strong acid list. We say that HCl "donates" its proton to the solution—very willingly in this case.
*HCl is a gas at room temperature and pressure.


Sodium hydroxide, NaOH, is one of the most commonly used strong bases. It, too, dissolves completely in water:
It forms a sodium cation and a hydroxyl anion, OH-. NaOH is said to "donate" a hydroxyl ion to the solution.
Sodium hydroxide is a common component of drain cleaners, and is also known by the common name, "lye". It is a white solid at room temperature and pressure. Base compounds are also called alkali compounds from time to time.
Water is the prototypical neutral compound. Pure water is what we define neutral to be. It is neither acidic nor basic. A closer look later will show us that it's actually both a weak acid and a weak base. We understand that, unlike the H-atom in HCl, the H-atoms in H2O are bound covalently,
and don't come off easily. Water is not an ionic compound, but it still dissociates. At any given time in a beaker of water, some molecules may be found undergoing the dissociation, known as the auto-ionization of water:
A key feature of acids and bases is that they can neutralize one-another. Consider the reaction between the strong acid HCl and the strong base NaOH:
This is typical of a neutralization reaction. The products of neutralization are a salt consisting of the liberated cation of the base and the anion of the acid, and water. Because simple salts don't contain ionizable protons or hydroxyl groups, they are neutral in solution, and of course water is neutral. A solution of NaCl in water, for example, is neutral.
We noted above that at any given time, some water molecules are dissociated into OH- and H+ according to the equation
Often, that equation is written as
where H3O+ is called the hydronium ion. We often write acid base equations using the hydronium ion because it more accurately reflects what actually happens inside an aqueous solution, but the simpler equation is usually perfectly adequate for our purposes. A free proton is never exactly "free" in water. It always associates, if only fleetingly, with one or more water molecules, yet is still able to move quickly through the liquid.
We can write the equilibrium constant expression for this reaction like this:

Now in a neutral solution [H+] = [OH-], so
[H+][OH-] = [H+][H+] = [H+]2 = 1.0 x 10-14,
thus in a neutral solution, [H+] = 1.0 x 10-7.
Now let's do something that may seem odd, ... and I'll explain later: Let's take the negative of the base-10 log of both sides of that last equation:
-log10 [H+]2 = -2 log10 [H+] = -log10 (1.0 x 10-14),
which gives
[H+] = 7.
We call this number, the negative of the base-ten log of the proton concentration, the pH of the solution. The pH of pure water is 7, and we refer to pH = 7 as the neutral pH.
In chemistry, the letter p stands for "take the negative base-ten log," -log10, for example:
pH = -log[H+]
pOH = -log[OH-]
pKw = -log[Kw]
Although we could use either pH or pOH to characterize the acidity or basicity of a solution, we use pH by convention. The reason we use the pH scale — a logarithmic scale — at all is that the range of possible proton concentrations is very broad, from nearly 10-14 M up to 10 M or more. On the pH scale a very acidic solution might have a pH of 1 while a very basic solution might have a pH of 14. These are manageable numbers, if we can just remember where they came from. At any rate, the pH scale is entrenched in how we do chemistry today.
Also note that a pH 4 solution has 10 times the proton concentration as a pH 5 solution. That's how a logarithmic scale works.
pH < 7 means acidic.
pH > 7 means basic.
pH = 7 means neutral.
A little algebra gives us a handy relation: Notice that because in aqueous solution, [H+][OH-] = 1.0 x 10-14, we can always calculate [H+] if we know [OH-], and vice-versa. We know that if we take the negative base-10 log of the Kw expression, we get:
-log ( [H+][OH-]) = -log(1.0 x 10-14)
Using one of the laws of logs, log(ab) = log(a) + log(b), we get
-log[H+] - log[OH-] = -log(1.0 x 10-14)
Now converting the -logs to "p" notation we obtain a very useful relationship between pH and pOH, one that you should memorize:
pH + pOH = 14
$$ \begin{align} pH &= -log(0.001) = 3 \\ pOH &= 14 - pH = 11 \end{align}$$
$$ \begin{align} pOH &= -log(0.00015) = 3.82 \\ pH &= 14 - pOH = 10.2 \end{align}$$
Strong acids and bases have a lot of street cred. They eat through things, and that's cool, but weak acids and bases are the business end of chemistry, especially in biological systems. Weak acids and bases are a little more difficult to deal with because they don't dissociate completely in solution. That means we have to be mindful of equilibria in which acids and bases aren't completely dissolved.
The proton concentration in a 1.0 M solution of the weak acid acetic acid (CH3COOH), for example, will be much lower than 1.0 M (what we would expect from complete dissociation to CH3COO- and H+) because the H+ doesn't detach as easily as it does from a strong acid. The anion CH3COO- is known as the acetate ion.
Let's do an example with acetic acid: Calculate the pH of a 0.1 M solution of acetic acid.
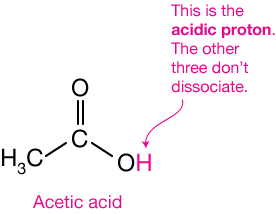
Acetic acid (left) is a weak organic acid known as a carboxylic acid. There are many such organic acids, differing by the identity of what is the CH3 group in the figure. If that is an H atom, for example, the acid is formic acid, the acid that gives red ant bites their sting.
The carboxyl group, -COOH, holds the acidic proton, the one that ionizes relatively easily, though not nearly as easily as the proton of a strong acid.

The dissociation equilibrium is
CH3COOH ⇌ CH3COO- + H+
(note the double arrow this time), with:

Here the equilibrium constant is written as Ka (short for "K-acid"). These and the Kb's of weak bases have been measured for almost any weak acid or base you will encounter. You can download a table of them here.
Now in a 0.1 M solution of acetic acid (often abbreviated CH3COOH), very little CH3COOH will actually dissociate because the equilibrium constant is so small. Look again at the Ka expression. In order for that fraction to be so small, the denominator must be quite a bit bigger than the numerator.
If x moles of CH3COOH dissociate, then there will be 0.1-x moles of undissociated CH3COOH left in solution at any time. Noting that the concentrations of acetate ion and protons must be the same from the stoichiometry of the dissociation reaction, we have

Multiplying both sides of this equation by the denominator on the left and gathering terms on one side, we get this quadratic equation:
x2 + 1.614 x 10-5 x - 1.614 x 10-5 = 0.
This can be solved by completing the square or by using a quadratic equation (Ax2 + Bx + C = 0) program on a calculator or computer, with A = 1, B =1.614 x 10-5, C = -1.614 x 10-5. We get x = 0.00252M.
Now pH = -log[H+], so pH = -log[0.00252] = 2.6. For comparison, the pH of a 0.1 M solution of a strong acid would be 1.
It's actually not necessary to solve the quadratic equation every time for weak acids. It turns out that the error in making a certain approximation is usually so small that we can tolerate it, and the approximation makes life with weak acids and bases easier. It's outlined below.
In example 3 above, we needed to solve the equation

which is a quadratic equation. While this isn't too difficult, especially if you've programmed your calculator to do it, there is a convenient approximation that will make life easier. Look at that equation again:

Now x is the concentration of protons, which, for a weak acid, ought to be very small.
We make the approximation that x is insignificant compared to 0.1 and just cross it out:

Now we just need to multiply both sides by 0.1 and take a square root. In this case the solutions are:
Exact pH = 2.598
with approximation pH = 2.896,
an error of about 10%.
As the dissociation constant becomes smaller (for weaker acids), this approximation gets better.
One of the most important weak bases is ammonia. It isn't a prototypical base because it doesn't directly supply a solution with OH- ions. Here is the aqueous equilibrium reaction:
We need to pause here to refine our definitions of acids and bases, because our previous one won't work for ammonia. This is the Brönsted-Lowry definition of acids and bases:
Acids are H+ (proton) donors
Bases are proton acceptors
This definition covers ammonia. Take another look at the dissociation equation. Ammonia "accepts" a proton from water (note that water acts as an acid in this case), leading indirectly to an increase in hydroxyl ion concentration. The Kb for ammonia is Kb = 1.778 x 10-5. The Kb expression is

Just like Ka values, Kbs are tabulated for many weak bases. Wikipedia is a pretty good source for chemical properties of all kinds, including acid-base properties.
The dissociation reaction is NH3 + H2O ⇌ NH4+ + OH-. Because this is a weak base, we know it doesn't dissociate completely, so we have to use the equilibrium constant expression (above). If we let x be the amount of NH3 that accepts a proton from water, then (0.001 - x) is the amount of NH3 left in solution, and we have:

Here we have employed our approximation to get
x = [OH-] = 0.001333 M
Now we can calculate the pOH:
pOH = -log(0.001333) = 2.88
... and finally the pH of the basic solution:
pH = 14 - pOH = 11.12
| 1. |
Calculate the pH of a 1.0 × 10-3 M solution of hydrochloric acid (HCl) SolutionHCl is a strong acid, HCl → H+ + Cl-, therefore it dissociates (comes apart into + and - ions in water) completely. $$ \begin{align} [H^+] &= 1.0 \times 10^{-3} \; M \\ pH &= -log[ H^+ ] \\ &= -log [10^{-3}] = \bf 3 \end{align}$$ pH 3 is a low pH (< 7), therefore this is an acidic solution. |
| 2. |
Calculate the pH of a 0.9 M solution of hydrobromic acid (HBr) SolutionHBr is a strong acid, HBr → H+ + Br-, therefore it dissociates (comes apart into + and - ions in water) completely. $$ \begin{align} [H^+] &= 9.0 \times 10^{-1} \; M \\ pH &= -log[ H^+ ] \\ &= -log [0.9] = \bf 0.046 \end{align}$$ pH 0.046 is a very low pH (< 7 and near the lowest pH possible), therefore this is a very acidic solution. |
| 3. |
Calculate the pH of a 2.234 × 10-6 M solution of potassium hydroxide (KOH). SolutionKOH is a strong base, KOH → K+ + OH-, and therefore dissociates completely into negative (they hydroxide ion, OH-) and positive ions in water solution. $$ \begin{align} [OH^-] &= 2.234 \times 10^{-6} \; M \\ pOH &= -log[ OH^- ] \\ &= 5.65 \\ pH &= 14 - pOH = \bf 8.35 \end{align}$$ pH 8.35 is a high pH (> 7), therefore this is a basic solution. |
| 4. |
Calculate the pH of 735 liters of a solution containing 0.34 moles of nitric acid (HNO3). SolutionFirst we have to calculate the concentration of the strong acid HNO3: $$\frac{0.34 \; mol \; HNO_3}{735 \, L} = 4.626 \times 10^{-4} \; M$$ Now HNO3 is a strong acid, and dissociates completely in water: HNO3 → H+ + NO3-. $$ \begin{align} [H^+] &= 4.626 \times 10^{-4} \; M \\ pH &= -log[ H^+ ] \\ &= -log [4.626 \times 10^{-4}] \\ &= \bf 3.33 \end{align}$$ Despite the large dilution factor (a small number of moles into 735 Liters), this is still quite an acidic solution, pH < 7. |
| 5. |
Calculate the pH of a 2.0 liter solution containing 0.005 g of HCl. SolutionFirst we need to calculate the concentration of the HCl. We have to convert 0.005g to moles, then divide by 2.0 Liters. $$ \begin{align} [HCl] &= \frac{0.005 \, g \; HCl \left( \frac{1 \; mol \; HCl}{37.45 \, g \; HCl}\right)}{2.0 \, L \; solution} \\ \\ &= 6.68 \times 10^{-5}\,M \end{align}$$ Now use that concentration, together with the fact that you kow HCl is a strong acid, which will dissociate completely, to find the pH: $$ \begin{align} [H^+] &= 6.68 \times 10^{-5}\,M \\ pH &= -log[ H^+ ] \\ &= -log [6.68 \times 10^{-5}] \\ &= \bf 4.18 \end{align}$$ |
| 6. |
Calculate the pH and pOH of a solution with a volume of 5.4 liters that contains 15 g of hydrochloric acid (HCl) and 25 g of nitric acid (HNO3). SolutionThere are two strong acids in this solution. We need to calculate the total number of moles of protons, then divide that by 5.4 L to get [H+] $$ \begin{align} 15 \, g \; HCl \left( \frac{1 \; mol \; HCl}{36.46 \, g \; HCl} \right) &= 0.411 \, mol \\ \\ 25 \, g \; HNO_3 \left( \frac{1 \; mol \; HNO_3}{63 \, g \; HNO_3} \right) &= 0.397 \, mol \end{align}$$ So the total number of moles is 0.411 + 0.397 mol = 0.808 mol. Now, $$[H^+] = \frac{0.808 \, mol \; H^+}{5.4 \, L} = 0.1495 \, M$$ So the pH is $$ \begin{align} pH &= -log[ H^+ ] \\ &= -log [0.1495 \, M] \\ &= \bf 0.82 \; \; \longleftarrow \; \text{ quite acidic} \\ pOH &= 14 - pH = 14 - 0.82 = 13.18 \end{align}$$ |
| 7. |
A swimming pool has a volume of 1 million liters. How many grams of HCl would you need to add to the pool to bring the pH from 7 down to 4? Assume that the volume of the HCl is negligible. SolutionAt pH 7, there will be no HCl present, assuming we're working with pure H2O. At pH = 4, the number of moles of H+ will be: $$ \begin{align} [H^+] &= \frac{x \; mol \; H^+}{10^6 \, L} \; \rightarrow \\ \\ x &= (1 \times 10^{-4})(1 \times 10^6) \\ &= 100 \; mol \; H^+ \end{align}$$ Now for every 1 mol of H+, there is 1 mol of HCl, so the number of grams of HCl we need to reduce the pH to 4 is: $$ \begin{align} 10^2 \; mol \; H^+ &\left( \frac{1 \, mol \; HCl}{1 \, mol \; H^+} \right) \left( \frac{36.46 \, g \; HCl}{1 \; mol \; HCl} \right) \\ \\ &= 3646 \, g \; HCl \\ &= \text{ 3.646 Kg HCl} \end{align}$$ |
| 8. |
Calculate the pH and pOH of a solution that was made by adding 400 ml of water to 350 ml of a 5.0 × 10-3 M NaOH solution. SolutionFirs we need the number of moles of NaOH in 350 ml (0.350 L) of a 1.74 × 10-3 M solution: $$0.350 \, L \left( \frac{5.0 \times 10^{-3} \; mol \; NaOH}{1 \; L}\right) \\ \\ = 1.75 \times 10^{-3} \text {moles NaOH}$$ Now the new concentration of NaOH, after dilution is: $$\frac{1.75 \times 10^{-3} \; mol\; NaOH}{(0.350 + 0.400) \, L} = 2.33 \times 10^{-2} \, M$$ So the pOH and pH are: $$ \begin{align} pOH &= -log(2.33 \times 10^{-2}) = 1.63 \\ pH &= 14 - pOH = 12.4 \end{align}$$ |
| 9. |
The active ingredient of aspirin is acetyl salicylic acid (C8H7O2COOH), which has Ka = 3.0 x 10-4. Acetyl salicylic acid is often abbreviated "ASA".
SolutionWe can abbreviate acetylsalicilic acid as HA, where A is the anion and H is the proton that comes off. The dissociation reaction is then HA ⇌ H+ + A- |
| 10. |
Papaverine hydrochloride (pap-HCl) is a salt of a weak base (papaverine) and a strong acid (HCl). It is a drug used as a muscle relaxant. Pap-HCl is a weak acid overall. At 25˚C, a 205 mM solution of pap-Hl has a pH of 3.31. Compute the Ka of pap-HCl. |
| 11. |
A 0.040 M solution of a weak acid (call it HA) has a pH of 4.70. Calculate the Ka and pKa of the acid. SolutionSolution here |

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.