Squeezing a function between functions
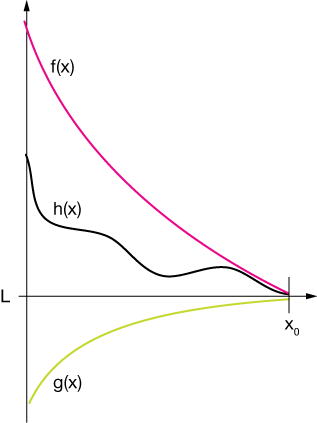
The squeeze theorem is another way to solve for tricky limits. It works by finding two functions, f(x) and g(x), that are, for every x in their domains, greater than and less than the target function, h(x), respectively. If f(x) and g(x) have the same limit at some value of interest, say x0, then so must h(x). More precisely, the theorem says
We seek
$$\lim_{x \to x_o} \, h(x).$$
Let $f(x) \gt h(x)$ for all x in the domains of f(x) and h(x), and let $g(x) \lt h(x)$ for all x in the domains of g(x) and h(x). Then if
$$\lim_{x \to x_o} \, f(x) = L \: \: \color{#E90F89}{\text{and}} \: \: \lim_{x \to x_o} \, g(x) = L,$$
then
$$\lim_{x \to x_o} \, h(x) = L$$
because it is "squeezed" between the two functions with known limits.
Asymptote
An asymptote is an imaginary line (of any slope, but often vertical or horizontal) which a function approaches as the independent variable approaches some value. The function graph always approaches the line, but will never meet it.
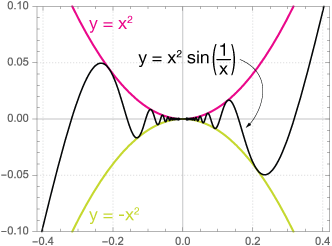
Example 1: $\lim_{x \to 0} \, x^2 sin \left( \frac{1}{x} \right)$
this is a difficult limit to find, but the squeeze theorem makes it easy. First, consider that
$$-1 \lt sin \left( \frac{1}{x} \right) \lt 1$$
for all x. Now because $x^2 \ge 0,$ we can multiply everything by $x^2$ to obtain
$$-x^2 \lt x^2 \, sin \left( \frac{1}{x} \right) \lt x^2$$
This is our recipe for the squeeze theorem, ilustrated in the figure. For all x, the function is less than $y = x^2$ and greater than $y = -x^2,$ which both have a value of zero at x = 0, therefore the value of our function at x = 0 is zero.
Example 2
We can also use the squeeze theorem to prove the trigonometric limit $\lim_{x\to 0} \frac{sin(x)}{x} = 1.$
Proving this limit using the squeeze theorem involves drawing a sector of the unit circle and two triangles related to it. The areas of the triangle can be placed in order to form an inequality, which can then be manipulated into the desired squeeze theorem statment. It begins with this sector.
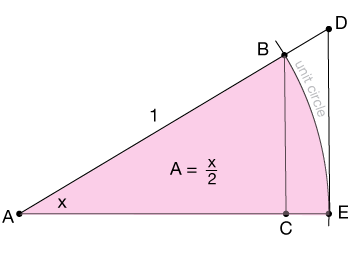
Now the area of a sector is found by taking its proportion to the area and angle (radians) of a full circle:
$$\frac{A}{\pi r^2} = \frac{x}{2 \pi}$$
which can be rearranged to give
$$A = \frac{x r^2}{2} \: \rightarrow \: = \frac{x}{2},$$
where in the last step, we realize that $r = 1$ for the unit circle.
Now our second triangle, the smallest of the three, is Δ ABE, shown here:

The height and width of this triangle are sin(x) and 1, respectively, giving an area of
$$a = \frac{1}{2} sin(x) \cdot 1$$
The largest triangle, ΔADE, is shown here
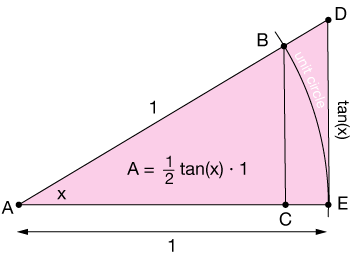
The tangent of angle x is the length of the opposite side divided by the adjacent, which has length 1, so the opposite side has length $tan(x).$ Thus the area of the largest triangle is
$$a = \frac{1}{2} tan(x) \cdot 1.$$
Now we can place these areas in order using inequalities:
$$\frac{1}{2} sin(x) \le \frac{x}{2} \le \frac{1}{2} tan(x)$$
Multiplication by 2 and conversion of tan(x) to sin(x)/cos(x) gives
$$sin(x) \le x \le \frac{sin(x)}{cos(x)}$$
Taking the reciprocal (and remembering to switch the inequalities) gives
$$\frac{1}{sin(x)} \ge \frac{1}{x} \ge \frac{cos(x)}{sin(x)}$$
Multiplication through by $sin(x)$ gives
$$1 \ge \frac{sin(x)}{x} \ge cos(x)$$
Now taking the limit as x → 0 squeezes the center term between 1 and 1, which requires it to also converge to a value of 1.
Example 3
Use the squeeze theorem to find the limit $\lim_{x \to \infty} \frac{cos(x)}{x - 1}.$
$$-1 \le cos(x) \le 1$$
That is, the cosine function oscillates between -1 and 1. Now divide all of these terms by $(x - 1)$:
$$\frac{-1}{x - 1} \le \frac{cos(x)}{x - 1} \le \frac{1}{x - 1}$$
The middle term contains the expression for which we seek the limit, and the outer limits are:
$$\lim_{x \to \infty} \frac{-1}{x - 1} \: = \: \lim_{x \to \infty} \frac{1}{x - 1} = 0.$$
So $\lim_{x \to \infty} \frac{cos(x)}{x - 1} = 0$ by the squeeze theorem. Here is a graph of the three functions, just so you can get an idea of what's going on.

Example 4
Use the squeeze theorem to find the limit $\lim_{x \to 0} x^2 \left[ 1 + sin \left( \frac{1}{x} \right)\right].$
$$-1 \le sin\left( \frac{1}{x} \right) \le 1$$
Now add 1 to all three parts of the inequality to get
$$0 \le 1 + sin \left( \frac{1}{x} \right) \le 2$$
One thing we know already is that $1 + sin \left( \frac{1}{x} \right)$ is bounded between 1 and 2, so multiplication by x2, with our limit as x → 0 should also be bounded. In other words, our squeeze-theorem attempt should work.
Multiplication of each element of the inequality by x2 gives
$$0 \le x^2 \left[ 1 + sin \left( \frac{1}{x} \right) \right] \le 2x^2$$
The outer limits are both zero, so the limit of interest is squeezed between zero and zero, so it, too, is zero. Here is a graph of the three functions in the neighborhood of x = 0, showing that the function (black) is squeezed between $y = 0$ and $y = 2x^2.$

Practice problems
Find the limits using the squeeze theorem.
| 1. |
$$\lim_{a\to \infty} \; \frac{sin(x)}{a}$$ Hint: begin with $-1 \le sin(x) \le 1.$ SolutionWe begin with $$-1 \le sin(x) \le 1,$$ then divide all three components of the inequality by a: $$\frac{-1}{a} \le \frac{sin(x)}{a} \le \frac{1}{a}$$ Now the outer limits are both zero, $$\lim_{x \to \infty} \, \frac{-1}{a} = \lim_{x \to \infty} \, \frac{1}{a} = 0,$$ so the limit = 0. |
| 2. |
$$\lim_{x\to 1} \; (x^2 + x - 2) \cdot cos \left( \frac{1}{x - 1} \right)$$ Hint: begin with $-1 \le cos \left( \frac{1}{x - 1} \right) \le 1$ SolutionWe begin with the inequality $$-1 \le cos \left( \frac{1}{1-x} \right) \le 1$$ Now multiplying both sides by $(x^2 + x - 2)$ gives $$ \begin{align} -x^2 &- x + 2 \le (x^2 + x - 2) \\[5pt] &\cdot cos \left( \frac{1}{1-x} \right) \le x^2 + x - 2 \end{align}$$ Now the outer limits evaluate to zero, so the interior limit is squeezed between 0 and 0, so $$\lim_{x \to 1} \, (x^2 + x - 2) \cdot cos \left( \frac{1}{1 - x} \right) = 0$$ Here's a graph of the functions.
|
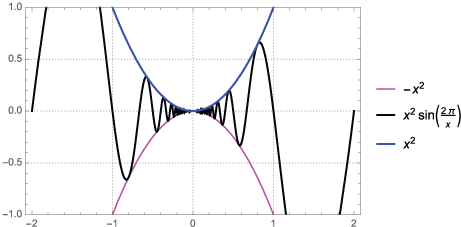
| 3. |
$$\lim_{x\to 0} \; x^2 \, sin \left( \frac{2 \pi}{x} \right)$$ Hint: begin with $-1 \le sin \left( \frac{2\pi}{x} \right) \le 1$ SolutionBegin with $$-1 \le sin \left( \frac{2 \pi}{x} \right) \le 1$$ Now multiply by x2 $$-x^2 \le x^2 \cdot sin \left( \frac{2 \pi}{x} \right) \le x^2$$ The outer limits both evaluate to zero, so the limit is zero. $$\lim_{x \to 0} \, x^2 \cdot sin \left( \frac{2 \pi}{x} \right) = 0$$ Here is a graph of the three functions.
|
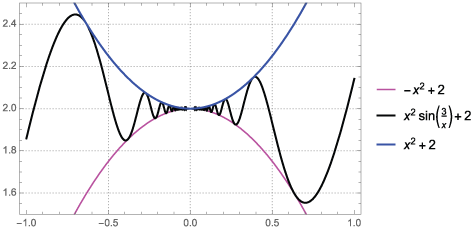
| 4. |
$$\lim_{x\to 0} \, x^2 sin \left( \frac{3}{x} \right) + 2$$
SolutionWe begin with the inequality $$-1 \le sin \left( \frac{3}{x} \right) \le 1$$ Now multiply through by x2: $$-x^2 \le x^2 \cdot sin \left( \frac{3}{x} \right) \le x^2$$ Then add 2 to all terms, $$-x^2 + 2 \le x^2 \cdot sin \left( \frac{3}{x} \right) + 2 \le x^2 + 2$$ Now both of the outer limits evaluate to 2, so the limit is $$\lim_{x \to 0} \, x^2 \, sin \left( \frac{3}{x} \right) + 2$$ Here is a graph of the three functions showing the squeezing:
|
| 5. |
$$\lim_{x\to 0} x \cdot sin(x)$$
SolutionStart with the inequality $$-1 \le sin(x) \le 1$$ Then multiply through by x: $$-x \le sin(x) \le x$$ The outer limits are both zero, so by squeezing, the innner limit is $$\lim_{x \to 0} \, x \cdot sin(x) = 0$$ Here is a graph of the function and the squeezing functions:
|
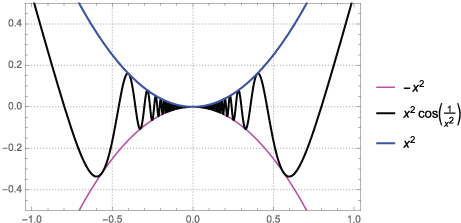
| 6. |
$$\lim_{x\to 0} \; x^2 \, cos \left( \frac{1}{x^2} \right)$$
SolutionStart with the inequality $$-1 \le cos \left( \frac{1}{x^2} \right) \le 1$$ Now multiply through by x2 to get $$-x^2 \le x^2 \cdot cos \left( \frac{1}{x^2} \right) \le x^2$$ Now the outer limits both evaluate to zero, so the inner limit is $$\lim_{x \to 0} \, x^2 \, cos \left( \frac{1}{x^2} \right) = 0$$ Here is a graph of the functions.
|

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2019, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.