Derivatives of compositions of functions:   $f(g(x))$

The chain rule is one of the most useful tools in differential calculus. Equipped with your knowledge of specific derivatives, and the power, product and quotient rules, the chain rule will allow you to find the derivative of any function.

The chain rule is a bit tricky to learn at first, but once you get the hang of it, it's really easy to apply, even to the most stubborn of functions. Knowing it will also allow you to forego the more cumbersome quotient rule in many cases, because any denominator $h(x)$ can be expressed as a multiple,$[h(x)]^{-1}$.

Each of the functions in the box on the right is a composition of functions, $f(x) = g(h(x))$. For example, in the first, $h(x) = x^2 - 4$ and the outer function is $g(x) = \text{sin}(x)$: $g(h(x)) = \text{sin}(x^2 - 4)$.

Derivation of the chain rule

To derive the chain rule, consider a function $y(t)$ that is actually a composition of functions, $y(x)$ and $x(t)$. It might be something like $y(t) = \text{cos}(3t^2)$, where $y(x) = \text{cos}(x)$ and $x(t) = 3t^2$. In terms of the changes in $y$ and $x$, we have:

$$ \require{cancel} \frac{\Delta y}{\cancel{\Delta x}} \frac{\cancel{\Delta x}}{\Delta t} = \frac{\Delta y}{\Delta x}$$

where the $\Delta x$ terms cancel to give the overall change in $y$ with respect to $t$. We can use the same cancellation in terms of differentials, but a word about that is in order:

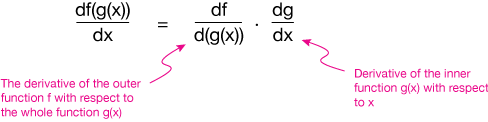
Learning the chain rule

It's easiest to learn the chain rule by working through examples. In the first two examples below, we'll substitute a "dummy variable" for the inner function, but you'll find that in no time you wont need to do that any more.

Example 1

Find the derivative of   $f(x) = \text{sin}(x^2)$

Solution: The outer function is $f(x) = \text{sin}(x)$ and the inner function is $g(x) = x^2$. Let's let $a = x^2$ and differentiate the outer function as $f(a) = \text{sin}(a)$:

$$f'(a) = cos(a)$$

Then we differentiate the inner function, $g'(x) = 2x$, and multiply it by $f'(a)$:

Example 2

Find the derivative of   $f(x) = (x^2 - 5)^3$

Solution: We'll do this one by making a substitution again. The outer function is $f(x) = x^3$ and the inner function is $g(x) = x^2 - 5$. Let's let $a = x^2 - 5$ and differentiate the outer function as $f(a) = a^3$:

$$f'(a) = 3 a^2$$

Example 3

Find the derivative of   $f(x) = (x^2 + x)^{1/2}$

Solution: Let's do this one without substitution of a placeholder variable and use the chain rule directly. The first step is to take the derivative of the whole outer function, treating the inner function $(x^2 + x)$ as a single unit.

Example 4

Find the derivative of   $f(x) = (x^2 - 4)^{-1}$

Solution: The outer function is $x^{-1}$ and the inner is $x^2 - 4$. The derivative is $f'(x) = -(x^2 - 4)^{-2}(2x)$, which can be simplified a bit, but I'll leave that to you.

Practice problems

Find the derivatives of these compound functions using the chain rule. You may have to also use the product or quotient rules.

1. $$f(x) = (x^3 + x^2 - x + 1)^3$$

   Solution

   Inner function:   $1 - x^3$

   Outer function:   $x^{\frac{1}{2}}$

   $$\begin{align} f'(x) &= \frac{1}{2} (1 - 3x)^{-\frac{1}{2}}(-3) \\[5pt] &= \frac{-3}{2 \sqrt{1 - 3x}} \end{align}$$

   Note: in calculus, it's almost always best to replace radicals with rational exponents.




2. $$f(x) = \frac{1}{x^2 - 1}$$

   Solution

   First rewrite the function as $f(x) = (x^2 - 1)^{-1}$

   Inner function:   $x^2 - 1$

   Outer function:  $x^{-1}$

   $$\begin{align} f'(x) &= -(x^2 - 1)^{-2} \cdot 2x \\[5pt] &= \frac{-2x}{(x^2 - 1)^2} \end{align}$$

   Note that this derivative could also be done by using the quotient rule directly. Try that and make sure you get the same derivative




3. $$f(x) = \frac{1}{1 + \text{cos}(x)}$$

   Solution

   First rewrite the function as $f(x) = (1 + \text{cos}(x))^{-1}$

   Inner function:   $1 + \text{cos}(x)$

   Outer function:  $x^{-1}$

   $$\begin{align} f'(x) &= -(1 + \text{cos}(x))^{-2} \cdot -\text{sin}(x) \\[5pt] &= \frac{\text{sin}(x)}{[1 + \text{cos}(x)]^2} \end{align}$$

   Note that this derivative could also be done by using the quotient rule directly. Try that and make sure you get the same derivative




4. $$f(x) = \frac{1}{\text{cos}^2(x)}$$

   Solution

   If we rewrite f(x) as $f(x) = (\text{cos}^2(x))^{-1}$, and realize that the funky shorthand we use for raising trig functions to powers actually means

   $$f(x) = [(\text{cos}(x))^2]^{-1},$$

   Then our function, written in the best shape to use the chain rule, is $f(x) = [\text{cos}(x)]^{-2}$

   Inner function:   $\text{cos}(x)$

   Outer function:  $x^{-2}$

   $$\begin{align} f'(x) &= -2 [\text{cos}(x)]^{-3} \cdot -\text{sin}(x) \\[5pt] &= \frac{2 \text{sin}(x)}{\text{cos}^3(x)} \end{align}$$

   This derivative could also be done by using the quotient rule directly. Try that and make sure you get the same result.




5. $$f(x) = x^2 + \text{cos}^2(x)$$

   Solution

   This is the sum of two functions; recall that the derivative of a sum is the sum of derivatives, so the derivative of the first term is just $2x$. The second function is a composite function:

   Inner function:   $\text{cos}(x)$

   Outer function:   $x^2$

   $$\begin{align} f'(x) &= 2x + 2\text{cos}(x)\cdot (-\text{sin}(x)) \\[5pt] &= 2[x - \text{sin}(x) \text{cos}(x)] \end{align}$$




6. $$f(\theta) = 3 \text{cot} (n\theta)$$

   Solution

   The inner function is very simple for this composite function $(3\theta)$, but it is there, so the chain rule is necessary.

   Inner function:   $3 \theta$

   Outer function:  $\text{cot}(x)$

   $$f'(\theta) = 3 n\cdot \text{csc}^2(n\theta)$$

   If you forgot the derivative of $f(x) = \text{cot}(x)$, it's easy to figure out just by rewriting it as $\frac{\text{cos}(x)}{\text{sin}(x)}$ and using the quotient rule.




7. $$f(x) = (2x - 3)^4(x^2 + x + 1)^4$$

   Solution

   This is a product of composite functions: $f(g(x)) \cdot f(h(x))$, where   $f(x) = x^4, \; g(x) = 2x - 2 \; \text{and} \; h(x) = x^2 + x + 1$

   $$\begin{align} f'(x) &= 4(2x - 3)^3 \cdot 2 \cdot (x^2 + x + 1)^4 \\[5pt] &+ (2x - 3)^4 \cdot 4 \cdot (x^2 + x + 1)^3 (2x + 1) \\[5pt] &= 4(x^2 + x + 1)^3\cdot(2x - 3)^3 \cdot \\[5pt] &[2(x^2 + x + 1) + (2x + 1)(2x - 3)] \end{align}$$




8. $$f(x) = \left(\frac{x^2 + 1}{x^2 - 1}\right)^3$$

   Solution

   Inner function:   $\frac{x^2 + 1}{x^2 - 1}$

   Outer function:  $x^3$

   After taking the simple derivative of the outer function, we'll have to multiply it by the quotient-rule derivative of the inner function.

   $$\begin{align} f'(x) &= 3 \left(\frac{x^2 + 1}{x^2 - 1}\right)^2 \left(\frac{x^2 - 1)\cdot 2x - (x^2 + 1)(2x)}{(x^2 - 1)^2}\right) \\[5pt] &= 3 \left(\frac{x^2 + 1}{x^2 - 1}\right)^2 \left( \frac{2x(x^2 - 1 - x^2 - 1)}{(x^2 - 1)^2}\right) \\[5pt] &= 3 \left(\frac{x^2 + 1}{x^2 - 1}\right)^2 \left( \frac{-2x}{(x^2 - 1)^2} \right) \end{align}$$




9. $$f(x) = \sqrt{\frac{x^2 + 1}{x^2 + 4}}$$

   Solution

   Rewrite the radical as a rational exponent:

   $$f(x) = \sqrt{\frac{x^2 + 1}{x^2 + 4}} = \left( \frac{x^2 + 1}{x^2 + 4}\right)^{\frac{1}{2}}$$

   Inner function:   $\frac{x^2 + 1}{x^2 + 4}$

   Outer function:  $x^{\frac{1}{2}}$

   After taking the simple derivative of the outer function, we'll have to multiply it by the quotient-rule derivative of the inner function.

   $$\begin{align} f'(x) &= 3 \left(\frac{x^2 + 1}{x^2 + 4}\right)^{-\frac{1}{2}} \left(\frac{x^2 + 4)\cdot 2x - (x^2 + 1)(2x)}{(x^2 + 4)^2}\right) \\[5pt] &= \frac{1}{2} \left(\frac{x^2 + 1}{x^2 + 4}\right)^{-\frac{1}{2}} \left( \frac{2x(x^2 + 4 - x^2 - 1)}{(x^2 + 4)^2}\right) \\[5pt] &= \frac{1}{2} \left(\frac{x^2 + 1}{x^2 + 4}\right)^{-\frac{1}{2}} \left( \frac{6x}{(x^2 + 4)^2} \right) \end{align}$$

   This could be simplified more, of course ...

Video examples

Here are eight examples (four videos) of chain rule derivatives. Enjoy! (OK, maybe that's overdoing it. I do hope they're helpful, though).

Example 1

Here are two examples of using the chain rule where the inner function [ $g(x)$ in $f(g(x))$ ] is a polynomial, and $f(x)$ is a simple power function like $f(x) = x^2$.

Minutes of your life: 0:00

Example 3

The first of these two examples involves a polynomial function that is the exponent of an exponential function, the second a polynomial inside a sine function.

Minutes of your life: 0:00