In order to solve related-rates problems, you really need to know how to differentiate implicitly. See the page on implicit differentiation to learn how.
It's all in the name
There is a class of problems in one-variable calculus called related rates problems. As the name suggests, the rate of change of one thing is related through some function to the rate of change of another. We can take advantage of that relationship and the fact that calculus is the mathematics of change to solve a whole bunch of new problems.
The general approach to a related-rates problem will be to identify the two things that are changing, to find some sort of relationship between them — often it will be s geometric relationship, to equate them and then take the derivative (these will be implicit derivatives) with respect to time of both sides.
The best way to learn related-rates problems is by doing examples, so here are a few.
Example 1
The sliding ladder problem
This is a classic problem in calculus. What happens at the top and bottom of a ladder that is sliding down the wall (and thus away from the wall at the bottom) is a little surprising: While the bottom of the ladder travels at a constant speed, the top accelerates downward. Weird.
The problem: A 6-meter ladder leans against a wall. The bottom of the ladder is 2 m from the wall at time $t=0$, and it slides away from the wall at the rate of $0.5 \;m/s$. Find the downward speed of the top of the ladder at any time, $t$, and at $t = 1$ second.

Notice that while the bottom of the ladder traces out constant intervals, the intervals against the wall increase between each equal time step. Here's the basic geometry:

$$\frac{dh}{dt} = ? \; \; \text{and} \; \; \frac{dx}{dt} = 0.5 \; m/s$$
where $t=$ time, and we take distance from the wall to be the positive direction. We can relate $x$ and $h$ through the Pythagorean theorem:
$$x^2 + h^2 = 36$$
Taking the derivatives with respect to time (that's what a rate is) of each side gives
$$\frac{d}{dt} x^2 + \frac{d}{dt} h^2 = \frac{d}{dt} 36$$
Notice that in the last term, the derivative of a constant is zero. Now taking the derivatives with respect to time gives:
$$2x \, \frac{dx}{dt} + 2h \, \frac{dh}{dt} = 0$$
Now rearrange to isolate $\frac{dh}{dt}:$
$$\frac{dh}{dt} = -\frac{x}{h} \frac{dx}{dt}$$
Finally, substitute for $\frac{dx}{dt}$ to get the final related-rates equation:
$$\frac{dh}{dt} = -0.5 \, \frac{x}{h} \; \text{m/s}$$
We can use the Pythagorean relationship above to express the downward velocity in terms of either $h$ or $x$. Let's use $h$, so: $x = \sqrt{36 - h^2},$ which gives
$$\frac{dh}{dt} = -0.5 \, \frac{\sqrt{36 - h^2}}{h} \; \text{m/s}$$
Here is a plot of the velocity at the top of the ladder vs. ladder height. At its full 6 m height (parallel to the wall), the ladder has zero velocity. As the height decreases to zero, the top accelerates downward (thus the negative velocity in the graph).
Related rates procedure
To solve related rates problems, consider the name. We need to find a relationship between two variables, an equation that relates them in some way. Then the word rate means a derivative with respect to time. Find the relationship, then use implicit differentiation to find the derivative of both sides with respect to time. Plug in any rate you know and solve.
Example 2
The conical tank
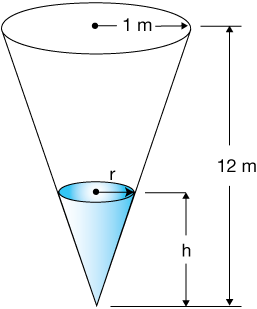
The problem: A conical tank with the dimensions shown is filled with liquid at a rate of 1.5 m3·min-1. At what rate is the water level rising when it passes a height of 5 meters? Sketch a graph of the rate as a function of time.
$$\frac{dh}{dt} = ? \; \; \text{ and } \; \; \frac{dV}{dt} = 1.5 \; m^3/min$$
What we know and don't know:
This problem is typical of a great many others in two ways. First, two rates are related (duh). In this case the rate of filling (or draining) is proportional in some way to the change in height of the liquid, measured as $h$, as shown. Second, while at first glance it's a two-variable problem [$V = f(r, \; h)$], those two variables are related by an equation, thus one variable can be eliminated to reduce the problem to a single variable one.
Then we take the time derivative of both sides, relating the rate of volume change to the rate of change of the height.
Implicit differentiation and the chain rule leads us to an expression for $f'(h)$ that can be used to find the rate of change of height at any time.
At a height of 5 meters, the rate is
$$\frac{dh}{dt}\bigg|_{h = 5} = \frac{216}{\pi (5)^2} = 2.75 \; m/min$$
The ratio of radius to height of the water cone is equivalent to that ratio of the whole cone, which we know:

Plugging our new expression for the radius into the volume formula gives
$$V_{cone} = \frac{\pi h^3}{3 \cdot 144} = \frac{\pi h^3}{432}$$
Now we take the derivative of both sides with respect to time:
$$\frac{d}{dt} V = \frac{d}{dt} \frac{\pi h^3}{432}$$
We know $dV/dt$, so that reduces to:
$$1.5 = \frac{3 \pi h^2}{432} \frac{dh}{dt}$$
where we've taken the implicit derivative with respect to time on the right. Then we solve for $dh/dt$:
$$\frac{dh}{dt} = \frac{1.5(432)}{3 \pi h^2} = \frac{216}{\pi h^2}$$
and the result is:
$$\frac{dh}{dt} = \frac{216}{\pi h^2}$$
The graphs below show the height of liquid as a function of time for this problem, and its derivative with respect to time. Note that each is drawn on its own set of axes. Even though it's often done, it is incorrect to superimpose the curves on the same graph; they have different y-axes. Make sure you understand the relationship between the height vs. time curve and its derivative.


Example 3
Tracking a rocket
Let's say you track the progress of a rising rocket using a clinometer, an instrument for measuring the angle between the line of sight (to the nose of the rocket here) and the level ground. The angle is labeled $\theta$ in the picture.
The problem: At a given moment, the angle between the nose of the rocket and the ground is 39˚ and is changing at a rate of 25˚·min-1. Calculate the velocity of the rocket at that instant.
Here's what we know and don't know:
$$\frac{dy}{dt} = ? \; \; \text{ and } \; \; \frac{d \theta}{dt} = 25˚ /s$$

The first trick is to find a relationship between $\theta$ and $y$, and we find it in trigonometry: $\tan(\theta) = y/5$. From there we differentiate both sides, plug in what we know and solve for the vertical velocity, $dy/dt$.
The key relationship between $y$ and $\theta$ is
$$tan(\theta) = \frac{y}{5}$$
Taking the derivative of both sides with respect to time,
$$\frac{d}{dt} tan(\theta) = \frac{d}{dt} \frac{y}{5}$$
gives us:

Now we solve for $dy/dt$ to get:
$$\frac{dy}{dt} = 125 \; sec^2(\theta)$$
Finally, plugging in our target angle of 39˚ gives us the answer we were seeking:
$$\frac{dy}{dt} = 125 sec^2(39˚) = 161 \; Km/s$$
By now these related rates problems should show a familiar pattern. I think they're fun because there's a definite method, but we still need to find our way through the specific algebra of each kind of problem.
Practice problems
| 1. |
A man 6 ft. tall is walking at 3 ft./s toward a street light hung 15 ft. above the ground. How fast is the length (s) of his shadow changing? How fast is the tip of his shadow moving? (Hint: similar triangles)
|
| 2. |
Corn kernels are being dumped from a funnel, forming a conical pile, the height of which is always 1/3 the diameter of its base. If the corn falls onto the pile at a rate of 2 m3·min-1, how fast is the pile rising when it is 1 m high?
|
| 3. |
A television camera is positioned 5 m from the edge of a track, as shown, in order to follow runners as they pass and approach the finish line. If the runner is moving at 5 m/s as he passes the finish line 10 meters away (where the lane numbers are), how fast (in degrees per second) must the camera be rotating just as it pans across the line?
|
Video examples
Here are two examples of how to solve related-rates problems.
Example 1
A weather balloon expands against reduced air pressure as it rises. Both the radius and volume change are proportional to the altitude.
Minutes of your life: 0:00
Example 2
A conical tank (point downward) is filled with liquid at a constant rate. The rate of filling is related to the rate of rise of the water level in the tank.
Minutes of your life: 0:00

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.





