Using calculus to learn more about the shapes of functions
In this section we'll learn how the tools of differential calculus can help us to learn much more about the graphs of functions than we could without it. Using calculus, we can determine just where maxima and minima of functions occur, and we can determine inflection points – points where the curvature of a graph changes.
Adding the first and second derivatives to our toolkit of curve sketching will be very valuable, but it's worth pausing here to emphasize this one thing about understanding the shape of a graph:
Old school!
There is no substitute for your basic pre-calculus skills when it comes to understanding the shape of the graph of a function. These skills include awareness of roots, asymptotes, holes, end behavior and symmetry. Don't forget them!
Maxima and minima of functions (extrema) – definitions
Before you move on, you should know this terminology — names of maxima and minima in the graph of a function:
- Global minimum — The global minimum is the lowest value of the function across its entire domain.
- Global maximum — The global maximum is the highest value of the function across its entire domain.
- Local minimum — a local minimum is the lowest value of a function in some local neighborhood, such as some defined interval [a, b].
- Local maximum — a local maximum is the highest value of a function in some local neighborhood.
The global or absolute maximum is the highest point on the graph of the function and the upper limit of its domain. The opposite is true for the global or absolute minimum.
A local max. or min. is just the highest or lowest point in an isolated region or "neighborhood."
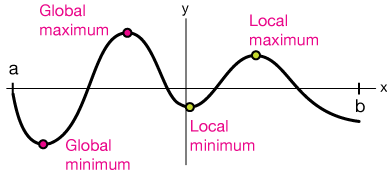
Note that if you're asked to find the maximum or minimum of a function on some closed interval like [a, b], that max or min just might be one of the endpoints, so be sure to check those in your search.
The table below gives more mathematical definitions of the maxima and minima.
| Point | If c is a number in the domain [a, b] of the function f, then f(c) is the |
| Global minimum | on [a, b] if f(c) ≤ f(x) for all x in [a, b] |
| Global maximum | on [a, b] if f(c) ≥ f(x) for all x in [a, b] |
| Local minimum | of f if f(c) ≤ f(x) when x is near c |
| Local maximum | of f if f(c) ≥ f(x) when x is near c |
| End points | On a closed interval, [ ], make sure to test the endpoints of the interval when checking for maxima or minima. They might, in fact, be the highest or lowest points in that interval. |
neighborhood (math)
In math, the neighborhood of a point in a function is a set of other points of the function to which one could move along the graph and not leave it.
Fermat's Theorem
To begin, let's recap an important theorem that was covered in the section on "existence theorems.", Fermat's theorem.
Fermat's theorem
If a function f has a local minimum or maximum at a point c, and if f'(c) exists, then f'(c) = 0.
Note: The fact that f'(x) = 0 does not necessarily mean that there is a local max. or min. at c. Fermat's theorem does not work in reverse. If there is a max. or min., then the derivative is zero. Existence of a zero derivative is not evidence of a max. or min.
One example of this caveat is the function f(x) = x3, shown below. This function has no maxima or minima, but f'(0) = 0, so the slope of the function is zero at x = 0. This particular point is an inflection point.

Fermat's theorem says that if a function has a local maximum or minimum (which could be global), then the derivative at that point is zero. It's not to difficult to prove Fermat's theorem, so let's do it.
Proof
Referring to the definition of the local maximum above, we see that if a maximum value lies at x = c, then f(x) must be larger than some other value of the function f(x + h), where h can be positive or negative. So:
$$f(c) \ge f(c + h)$$
which rearranges to:
$$f(c + h) - f(c) \le 0$$
We can divide both sides of this inequality by h to make this look like a derivative, then take the limit as h → 0+ from the right:
$$\lim_{h\to 0^+} \frac{f(c + h) - f(c)}{h} \le \lim_{h\to 0^+} (0)$$
Now we have assumed that f'(c) exists, so the limit from the right must equal the limit in general:
$$\lim_{h\to 0^+} \; \frac{f(c + h) - f(c)}{h} \le 0$$
The expression on the left is f'(c), so we have:
$$f'(c) \le 0$$
Now we could also do the same proof using the limit from the left, which would lead us to the inequality f'(c) ≥ 0, and we'd have the double inequality,
$$0 \le f'(c) \le 0$$
The only way that both inequalities can be true is for f'(c) to be equal to zero, so we have proved Fermat's theorem.
The derivative and slope
Remember that the derivative of a function gives its slope at any differentiable point in its domain.
The derivative of a rising function (positive slope) is positive, and
the derivative of a falling function (negative slope) is negative.
We proved this using the mean value theorem in another section. We can extend this thinking to understand that a function rises to left side of a maximum and falls off to the right, and a function falls to the left of the minimum and rises to its right. Of course, we have to be careful not to stray too far away from a max. or min. for that argument to hold. We generally speak of a "neighborhood" tight around the max. or min.


Critical points
Critical points of a function are points (possibly none or one) at which the first derivative of the function is zero.
As we saw in Fermat's theorem, a critical point might be a maximum or minimum of a function, or neither.
We'll eventually develop some ways to find out which, and to find out what a critical point might signify if it's not a max or min.
We find critical points simply by setting the first derivative equal to zero and solving for the roots: f'(x) = 0
Critical points
The critical points of a function are the zeros (or roots) of its first derivative.
Sometimes critical points are called critical numbers.
Example 1
Find the x-coordinates of the maxima and minima of $f(x) = -x^3 + 4x^2 + 4x - 16$
We begin by noting that this function can be factored by grouping:
$$ \begin{align} f(x) &= -x(x^2 - 4) + 4(x^2 - 4) \\ &= (4 - x)(x^2 - 4) \\ &= (4 - x)(x + 2)(x - 2) \end{align}$$
Real roots at x = 4, ±2
We can then sketch a quick graph with just the roots:

Now take the derivative of the function,
$$f'(x) = -3x^2 + 8x + 4$$
and set it equal to zero to find the critical points:
$$3x^2 + 8x + 4 = 0$$
Solving this quadratic equation by completing the square (or equivalently, using the quadratic formula, we get:
$$ \begin{align} 3x^2 + 8x + 4 &= 0 \\ \\ x^2 - \frac{8}{3} x + \left( \frac{4}{3} \right)^2 &= \frac{16}{9} + \frac{12}{9} \\ \\ \left( x - \frac{4}{3} \right)^2 &= \frac{28}{9} \\ x &= \frac{4 ± 2\sqrt{7}}{3} \end{align}$$
The two critical points are approximately x = -0.4 and x = 3.1, which match the minimum and maximum in our sketch, but now we know the x-coordinates exactly.
For a cubic equation, where we already know the end behavior and thus the order of the min. and max., we expect that critical points will correspond (for a positive leading coefficient) to the minimum on the left and the maximum on the right, both local.
We can confirm this, however by checking that for the minimum, the slope is negative on the left and positive on the right, and indeed, f'(-2) < 0 and f'(1) > 0. For the maximum, the slope on the left is positive, f'(2) > 0 and the slope on the right is negative, f'(4) < 0.
Here is the calculated graph of f(x). Hopefully you can see that by augmenting your pre-calculus curve sketching skills with calculus, you can learn a little more about the graph of a function.
But at the same time, don't forget that you could already say a lot about this graph with just those pre-calculus skills.
In the next example, we'll use that to find the solution to an optimization problem that, until now, you could probably only have solved by estimation with a computer or calculator.

Why do I need to learn to sketch curves if I can always just graph them on a computer?

There is no guarantee that the person who programs a calculator or computer (e.g. enters the function or data) does so without error. My hope for you is that you can be the person in the room who says, "wait a minute ... that can't be right ... " People make mistakes (and always will), so don't trust blindly in what your computer or calculator says. Be in a position to check it out, maybe not in great detail, but at least qualitatively, by applying your most excellent curve sketching skills.
Understanding the graphs of a function and its derivative
Remember that the derivative gives the slope of a function at any point in its domain. Therefore when the slope of a function is negative, like the region between -∞ and -1 for f(x), the graph of the derivative should lie below y = 0, which it does (red curve). Follow this trend across the graph, through all of its regions of negative and positive slope. Wherever the slope of f(x) is increasing the graph of the derivative is positive; likewise for decreasing regions.
Next, sometimes the derivative graph passes through zero. That means f(x) has zero slope at those points. Zero is the slope of a horizontal tangent, which occurs at extrema or critical points. We always have to be careful of exceptions, however. In fact, this function has a zero in its derivative at x = 1 with no corresponding maximum or minimum there.
We can use the first derivative to determine whether a particular extreme value is a maximum or a minimum:
- If the slope on the left side of an extreme value is negative and that on the right is positive, the extreme value is a minimum.
- If the slope on the left side of an extreme value is positive and that on the right is negative, the extreme value is a maximum.
On both sides of x = 1 the slope of f(x) is negative except at x = 1, where it is zero. That means it can't be a maximum or a minimum (a case where the reverse of Fermat's theorem wouldn't work). The slope of the function must change sign on either side of a maximum or a minimum.
Practice problems
Find the critical points of each of these functions. Determine whether each is a minimum, a maximum or neither.
| 1. |
$f(x) = 3 - \frac{1}{4} x$ Solution$$f'(x) = -\frac{1}{4}$$ This derivative is constant, so it has no zeros. (-¼ is never equal to zero). So this function has no critical points, and therefore no maxima or minima. That make sense because f(x) is a line with constant slope m = -¼ and y-intercept y = 3. |
| 2. |
$f(x) = sin(x) \phantom{000} 0 \le x \le \frac{3\pi}{2}$ Solution
|
| 3. |
$f(x) = \frac{x - 1}{x^2 - x + 1}$ Solution$$ \begin{align} f'(x) &= \frac{(x^2 - x + 1)(1) - (x - 1)(2x - 1)}{(x^2 - x + 1)^2} \\[5pt] &= \frac{x^2 - x + 1 - 2x^2 + x + 2x - 1}{(x^2 - x + 1)^2} \\[5pt] &= \frac{-x^2 + 2x}{(x^2 - x + 1)^2} \end{align}$$ Now the zeros of a fraction are the zeros of the denominator (because we could just multiply both sides by the denominator to get rid of it), so the critical points are $$ \begin{align} -x^2 + 2x &= 0 \\[5pt] x(2-x) &= 0 \\[5pt] x &= 0, \; 2 \: \color{#E90F89}{\longleftarrow \: \text{critical pts.}} \end{align}$$ Now check some convenient points on either side of these critical points to determine whether each is a maximum or minimum: $$ \begin{align} f'(-1) &\lt 0 \\[5pt] f'(0) &= 0 \color{#E90F89}{\leftarrow \: \text{minimum}} \\[5pt] f'(1) &\gt 0 \\[5pt] f'(2) &= 0 \color{#E90F89}{\leftarrow \: \text{maximum}} \\[5pt] f'(3) &\lt 0 \end{align}$$ Minimum: slope changes from negative to positive as we move from left to right across the critical point; Maximum: the opposite is true. |
| 4. |
$f(x) = x^{\frac{1}{4}} - x^{\frac{3}{4}}$ Solution$$f'(x) = \frac{1}{4} x^{-\frac{3}{4}} - \frac{3}{4} x^{-\frac{1}{4}}$$ Setting the derivative equal to zero and solving gives one critical point: $$ \begin{align} \frac{1}{4} x^{-3/4} - \frac{3}{4} x^{-1/4} &= 0 \\[5pt] x^{-3/4} &= -3 x^{-1/4} \\[5pt] x^{-3/4} &= 3x^{-1/4} \\[5pt] \frac{x^{1/4}}{x^{3/4}} &= 3 \\[5pt] \frac{1}{x^{1/2}} &= 3 \\[5pt] x^{1/2} &= \frac{1}{3} \\[5pt] x &= \frac{1}{9} \end{align}$$ Now test the point: $$ \begin{align} f' \left( \frac{1}{10} \right) &= 0.29 \gt 0 \\[5pt] f'\left( \frac{1}{9} \right) &= 0 \color{#E90F89}{\leftarrow \: \text{maximum}} \\[5pt] f' \left( \frac{2}{9} \right) &= -1.28 \lt 0 \end{align}$$ Here is a plot of the function showing its one maximum: |
| 5. |
$f(x) = 2x - tan(x) \: \text{ on } \: [0, 2\pi]$ Solution$$f'(x) = 2 - sec^2(x)$$ Now find the zeros (roots): $$ \begin{align} 2 - sec^2(x) &= 0 \\[5pt] sec^2(x) &= 2 \\[5pt] sec(x) &= ±\sqrt{2} \\[5pt] cos(x) &= ±\frac{\sqrt{2}}{2} \\[5pt] x &= \frac{\pi}{4}, \, \frac{3\pi}{4}, \, \frac{5\pi}{4}, \, \frac{7\pi}{4} \end{align}$$ There are an infinite number of solutions, but those are the four on the (arbitrary) interval [0, 2π] Here is a cosine graph just to help you find those critical points.
And here is a graph of the function showing the four solutions on this interval:
|
| 6. |
$f(x) = \sqrt{4 - x^2}$ Solution$$ \begin{align} f'(x) &= \frac{1}{2} (4 - x^2)^{-1/2}(-2x) \\[5pt] &= \frac{-x}{\sqrt{4 - x^2}} \end{align}$$ Now the derivative is only zero when x = 0, the one critical point. Now check the critical point: $$ \begin{align} f'(-1) &\gt 0 \\[5pt] f'(0) &= 0 \color{#E90F89}{\leftarrow \: \text{maximum}} \\[5pt] f'(1) &\lt 0 \end{align}$$
The graph is the top half of a circle of radius 2 with a maximum at x = 0. |
| 7. |
$-2x^3 + 54x + 5$ Solution$$f'(x) = -6x^2 + 54$$ Setting the derivative equal to zero gives two critical points: $$ \begin{align} 6x^2 &= 54 \\[5pt] x^2 &= 9 \\[5pt] x &= ±3 \end{align}$$ With polynomials, it's easy enough to do the 2nd derivative test to find out whether critical points are maxima or minima. $$ \begin{align} f''(x) &= -12x \\[5pt] f''(-3) &\gt 0 \: \text{so x = -3 is a minimum} \\[5pt] f''(3) &\lt 0, \: \text{ so x = 3 is a maximum} \end{align}$$ |
| 8. |
$f(x) = 3x^4 - 4x^3 - 12x^2 + 1$ Solution$$ \begin{align} f'(x) &= 12x^3 - 12x^2 - 24x \\[5pt] &= 12x (x^2 - x - 2) \\[5pt] &= 12x (x - 2)(x + 1) \end{align}$$ The zeros are $x = 0, -1, 2.$ We can use the second-derivative test to check these critical points: $$ \begin{align} f''(x) &= 36x^2 - 24x - 24 \\[5pt] f''(-1) &\gt 0, \: \text{so x = -3 is a minimum} \\[5pt] f''(0) &\lt 0, \: \text{so x = 0 is a maximum} \\[5pt] f''(2) &\gt 0, \: \text{so x = 2 is a minimum} \end{align}$$ |
The second derivative and the shape of a graph
The second derivative
The second derivative of a function is the derivative of its derivative.
$$f''(x) = \frac{d}{dx} \left(\frac{df}{dx} \right) = \frac{d^2}{dx^2} f(x) = D_x^2 f(x)$$
The second derivative indicates the curvature of a function. It describes the change in the slope. If a graph is concave-upward, then the slope is increasing. If it is concave downward, the slope is decreasing. These relationships or true whether the actual slope (the first derivative of f) is positive or negative.
The graphs to the right show the same function we plotted above, but this time compared to the graph of its second derivative. In this comparison, notice that every zero (f''(x) = 0) in the graph of the second derivative matches an inflection point in the graph of f(x), a point where the curvature changes between concave upward and concave downward.
The zeros in f''(x) all class with inflection points. In particular, the zero at x = 1 confirms the inflection point we already knew.
It is possible, however, that a zero in the 2nd derivative of a function does not indicate an inflection point. For example, the function g(x) = x4 has a zero at x = 0 in its second derivative, g''(x) = 12x2, but that point is actually the global minimum of that function, with concave-up curvature on either side. We must be cautious when basing conclusions about inflection points on the second derivative.
Finally, the second derivative can supply more information about whether an extremum (singular of extrema) is a relative maximum or minimum:
For an extremum at a point c in the domain of f(x),
- f''(c) > 0 for a relative minimum
- f''(c) < 0 for a relative maximum.
Inflection point
Inflection point — a point in a graph at which the curvature changes between concave-upward and concave-downward.
The general approach to curve sketching
Now we have another tool in our toolbox for understanding the shape of a graph: Perform the usual algebraic analysis, then use the first and second derivatives to find extrema and inflection points.
- Use your pre-calculus skills: Determine whether function has any asymptotes or other discontinuities like holes, determine the behavior of the extreme ends of the function, and find any points that are easy to find - the y-intercept, for example; determine the roots (x-intercepts) if possible.
- Find the 1st the first derivative and solve f'(x) = 0 to find the critical points.
- Decide whether f'(x) is negative or positive on each interval between critical points. Make sure that this information is consistent with what you determined in steps 1 & 2.
- Find the 2nd derivative if possible (sometimes this can be a mess, so be sure you really need to!) If f''(x) > 0, the function is concave upward; if f''(x) < 0, it's concave downward. f''(x) = 0 at an inflection point (usually).
- Combine all of these steps and make sure that all of the information you have about the function is consistent. It has to be.
Some of the implications of the first and second derivatives on curve shape are summarized in the table below.
Example 2 – Rational function
Sketch an accurate graph of f(x) including the locations of any asymptotes, maxima, minima and inflection points.
$$f(x) = \frac{x^2 - 2x + 4}{x - 2}$$
First, let's take a look at the numerator. The zeros of the numerator are the zeros of a rational function. In this case, the discriminant is less than zero, so this function has no real roots.
$$ \begin{align} b^2 - 4ac &= (-2)^2 - 4(1)(-2) \\ &= 4 - 8 = -4 \end{align}$$
When the degree of the denominator is one greater than the degree of the numerator, the function has a linear slanted asymptote, which we find by long division:
$$ \require{enclose} \begin{array}{rll} x\phantom{00000000} \\[-3pt] x - 2 \enclose{longdiv}{x^2 - 2x + 4}\kern-.2ex \\[-3pt] \underline{x^2 - 2x\phantom{000}} \\[-3pt] 4 \\[-3pt] \end{array}$$
The slanted asymptote is y = x. The denominator has a zero at x = 2, so there's a vertical asymptote there:

Now to find the critical point(s) by taking the first derivative. By the quotient rule, we start here:
$$f'(x) = \frac{(x - 2)(2x - 2) - (x^2 - 2x + 4)}{(x - 2)^2}$$
Expanding, we get:
$$f'(x) = \frac{2x^2 - 6x + 4 -x^2 + 2x - 4}{(x - 2)^2}$$
... which reduces to:
$$f'(x) = \frac{x(x - 4)}{(x - 2)^2}$$
Critical pts. at x = 0, x = 4
The zeros of f'(x) are the zeros of the numerator above, x = 0 and x = 4, so those are candidates for maxima or minima. Now we take the second derivative for two reasons: (1) to learn about the curvature and look for inflection points and (2) to test the critical points to see whether they're maxima or minima.
$$f''(x) = \frac{d}{dx} \frac{x^2 - 4x}{(x - 2)^2}$$
By the quotient rule the second derivative is:
$$f''(x) = \frac{(x - 2)^2(2x - 4) - (x^2 - 4x)(2)(x - 2)}{(x - 2)^4}$$
We can divide away one (x - 2) to get
$$f''(x) = \frac{(x - 2)(2x - 4) - 2(x^2 - 4x)}{(x - 2)^3}$$
Expanding the numerator and canceling where possible gives us a constant numerator
$$f''(x) = \frac{2x^2 - 8x + 8 - 2x^2 + 8x}{(x - 2)^3}$$
The constant numerator means that the function has no inflection points, because these have to be zeros of the 2nd derivative.
$$f''(x) = \frac{8}{(x - 2)^3}$$
The second derivative test on the critical point x = 0 shows that it's a maximum. The test on x = 4 says that it's a minimum.
$$ \begin{align} f''(0) &= 1 \; \color{#e90f89}{\text{ x = 0 is a maximum}} \\ f''(4) &= 1 \; \color{#e90f89}{\text{ x = 4 is a minimum}} \end{align}$$
Here's the graph of our function. It has a slant asymptote (y = x) and a vertical asymptote at x = 2. The function is discontinuous and therefore not differentiable at x = 2. It has no holes. It has a relative maximum at x = 0 and a relative minimum at x = 4.

The calculus we did is completely consistent with what we discovered about this function using only our algebra toolkit, and it extends that technique by allowing us to find the exact location of the relative maximum and minimum.
Example 3 – Another rational function
Sketch an accurate graph of f(x) including the locations of any asymptotes, maxima, minima and inflection points.
$$f(x) = \frac{x^2 - x - 6}{x - 1}$$
First, use your precalculus skills to find root(s) (the zeros of the numerator) and vertical asymptote(s), if they exist:
$$f(x) = \frac{(x - 3)(x + 2)}{x - 1}$$
So our graph will cross the x-axis only at x = -2 and x = 3, and because those are single roots (the binomial appears only once, i.e. is not squared, cubed ...), the graph crosses right through the x-axis there. There will also be a vertical asymptote at x = 1.
Next, notice that the degree of the numerator is one larger than the degree of the denominator, which means the function has a slanted linear asymptote. We find its equation by polynomial long division, up to the remainder:
$$ \require{enclose} \begin{array}{rll} x\phantom{00000000} \\[-3pt] x - 1 \enclose{longdiv}{x^2 - x - 6}\kern-.2ex \\[-3pt] \underline{x^2 - x\phantom{000}} \\[-3pt] -6 \\[-3pt] \end{array}$$
Next, take the derivative of f(x) and set it equal to zero. This will require a bit of simplification:
$$ \begin{align} f'(x) &= \frac{(x - 1)(2x - 1) - (x^2 - x - 6)}{(x - 1)^2} \\[5pt] f'(x) &= \frac{2x^2 - 3x + 1 - x^2 + x + 6}{(x - 1)^2} \\[5pt] f'(x) &= \frac{x^2 - 2x + 7}{(x - 1)^2} \end{align}$$
Now the zeros of the derivative are the zeros of the numerator, and to find those, we complete the square (or equivalently, solve the quadratic equation.
$$ \begin{align} x^2 - 2x + 7 &= 0 \\[5pt] x^2 - 2x &= -7 \\[5pt] x^2 - 2x + 1^2 &= -7 + 1^2 \\[5pt] (x - 1)^2 &= -8 \\[5pt] x &= 1 ± i\sqrt{8} \end{align}$$
Note: I could have just noticed that the discriminant, $b^2 - 4ac$ is less than zero, and thus the derivative has imaginary roots, but I enjoy completing the square!
The roots of the derivative are imaginary, so this function has no critical points, and therefore has no maxima or minima.
Because we already know everything there is to know about the curvature of this graph, we won't need the second derivative, by you might confirm for yourself that the only zero is at x = 1, the point at which the curvature changes, but this point is undefined in the function (vertical asymptote).

This example is another good reminder not to forget about those precalculus skills. We found the y-intercept, the equation of the slant asymptote and the roots using algebra, and the facts they revealed basically established the shape of the graph. It's also worth thinking about the relative simplicity of the function — it just cant have a tremendous number of "wiggles" because its highest power is 2.
We used the first derivative to establish that there were no maxima or minima, sealing the deal on the shape of the graph; without any turning points and the other constraints we've stacked up, we've got all of the important features needed to sketch the graph. Absence of maxima or minima allows us to conclude that this function does not cross the slant asymptote for x near zero. If it did, that would create a "bump".
Example 4 – Polynomial function

So the function can be rewritten as the binomial (x - 1) multiplied by the resulting quadratic, which is then factorable, and we get three roots:
$$ \begin{align} f(x) &= (x - 1)(x^2 - x - 6) \\[5pt] &= (x - 1)(x + 2)(x - 3) \end{align}$$
Now taking the derivative, and setting it equal to zero, we can find the critical points. For a cubic we expect, at most, a local minimum and a local maximum, two critical points:
$$ \begin{align} 3x^2 - 4x - 5 &= 0 \\[5pt] 3x^2 - 4x &= 5 \\[5pt] x^2 - \frac{4}{3} x = \frac{5}{3} \\[5pt] x^2 - \frac{4}{3} x + \left( \frac{2}{3} \right)^2 = \frac{15}{9} + \frac{4}{9} = \frac{19}{9} \\[5pt] x = \frac{2 ± \sqrt{19}}{3} \end{align}$$
Because (precalculus!) we know the end behavior, we know that the minus solution is a maximum and the plus solution is a minimum. Now the second derivative is:
$$f''(x) = 6x - 4$$
We can use f''(x) to test our two critical points, just to confirm our precalculus intuition:
$$f''\left( \frac{2 + \sqrt{19}}{3} \right) = 2 \sqrt{19} \\[5pt] \color{#e90f89}{\gt 0 \implies \text{ relative minimum}}$$
$$f''\left( \frac{2 + \sqrt{19}}{3} \right) = -2 \sqrt{19} \\[5pt] \color{#e90f89}{\lt 0 \implies \text{ relative maximum}}$$
Finally, setting the second derivative equal to zero, we find that x = 2/3 is a candidate to be an inflection point. There's no need checking that the curvature changes on either side, because we know that has to be true for a cubic function.
$$ \begin{align} f''(x) &= 6x - 4 = 0 \\[5pt] x &= \frac{2}{3} \end{align}$$
x = ⅔ is the location of a possible inflection point. We always need to confirm that by checking the curvature to the left and right.
Finally, here's the graph with all of the meaningful points sketched in:

Example 5 — An absolute-value function
Explore the graph of the absolute-value function $f(x) = |1 - x^2|$
$$f'(x) = \frac{-2x(1 - x^2)}{|1 - x^2|}$$
Setting that equal to zero to find the critical points,
$$\frac{-2x(1 - x^2)}{|1 - x^2|} = 0$$
We get three critical points. At x = ±1, the derivative is not defined, but at zero, we have a maximum, which we need not check because of our knowledge of the symmetry of the underlying quadratic function g(x) = 1 - x2.
$$ \begin{align} -2x (1 - x^2) &= 0 \\[5pt] x &= ±1, 0 \end{align}$$
The derivative is undefined at x = ±1, and x = 0 is a maximum. The graph of both the function and its derivative are shown.

Derivative of an absolute-value function

Example 6 — Root function
$$f(x) = 3x^{\frac{1}{3}}$$
The derivative, because of the x2 in the denominator, is greater than zero for all x, so there are no critical points, and therefore no maxima or minima:
$$f'(x) = x^{-\frac{2}{3}} = \frac{1}{(x^2)^{1/3}} \; \color{#E90F89}{\text{ > 0 for all x ≠ 0}}$$
The second derivative is found using the chain rule with negative exponents or the quotient rule, and it tells us what we need to know about the concavity of the function:
$$ \begin{align} f''(x) &= -\frac{2}{3} x^{-\frac{5}{3}} \\[5pt] &\gt 0 \text{ for } x \lt 0 \; \; \color{#e90f89}{\text{ Concave up}} \\[5pt] &\lt 0 \text{ for } x \gt 0 \; \; \color{#e90f89}{\text{ Concave down}} \\[5pt] &\text{undefined for x = 0} \end{align}$$
Everything is consistent with the graph below.


![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.






