This section depends on your solid understanding of continuous random variables, so if you're not up to speed on those, go that section first.
The concept of a probability distribution is very important in statistics and probability. You might say it's the very foundation of statistics. By the way, you might get stuck on the word "distribution." It's a old word we've inherited from studies of things that involve random chance. Don't get hung up on the word, and in time, it will probably make a lot of sense to you.
The graph below illustrates the concept of probabilty distribution. It's a Census Bureau study of the heights of American women ages 30-39. The actual discrete data is represented by the purple bars: the higher the bar, the more women (as a percent of all women 30-39) of that height. That is, the higher the bar, the greater the probability of a woman you meet aged 30-39 being that height.
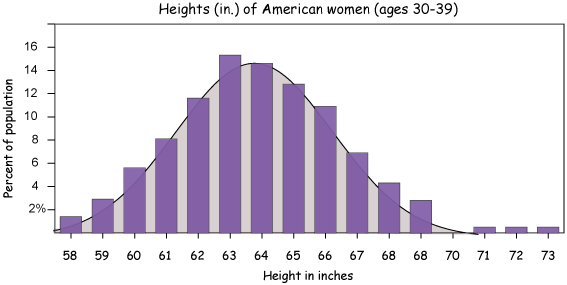
You can see from the graph that the mean height is about 64 inches (5'-4"). You can see that there are about as many women taller and shorter than the average, and that the numbers of women taller and shorter than the average falls fairly smoothly away from it. And there are more women of heights closer to the average than those of heights much shorter or taller than it.
The underlying curve (gray-shaded area) is a special curve we call the normal distribution or the Gaussian distribution, and it shows what the data would likely look like if we had a great many data points (see law of large numbers) – and indeed this was quite a large study. We would also head toward a more continuous curve if we divided our height "bins" more finely, say in increments of 1/4-inch units or smaller.
Discrete means individually separate and distinct. In mathematics, a discrete varable might only take on integer values, or values from a set {a, b, c, ... d}. In quantum mechanics, things the size of atoms and molecules can have only discrete energies, E1 or E2, but nothing in between, for example.
There are several types of probability distributions with which you should be familiar, each useful in a particular situation. We'll take a tour through them in the next section. The most ubiquitous is the normal or Gaussian distribution, the basis for much of any statistical analysis you're likely to encounter out in the world.
The uniform probability distribution is one in which the probability of any outcome of a probability "experiment" is the same. A good example is the rolling of a single fair die (fair means equal chance of rolling 1, 2, 3, 4, 5 or 6).
The probability of rolling a 1 is the same as that for rolling a 2 or 3, 4, 5 or 6. for each there is a 1 in 6, or ⅙ chance. We can sketch a graph of these discrete outcomes like this:
Now any probability distribution must also capture the idea of an assured outcome, that is, that when the experiment (tossing the die) is performed, some outcome is assured. The die will come up with a result.
The total probability, therefore, must sum to 1. In this case, we have six possible outcomes, each with a ⅙ probability, so the total area of our rectangular probability distribution graph (below) is 1. We would refer to this as a normalized distribution.
Coin tossing is another example of a probability experiment with a uniform distribution of outcomes. There is a ½ probability of tossing heads and a ½ probability of tossing tails, the only two possible outcomes (we can approximate the probability of a coin landing on its edge to zero). The two probabilities sum to 1.
We might also have a uniform distribution of continuous outcomes, where our probability experiment could give any result between x = a and x = b, with equal likelihood, as in the graph below.
This is the most general representation of the uniform distribution.
Now let's derive formulas for the average and variance $(\sigma^2)$ of this distribution. The average of a distribution over a range [a, b] is obtained by doing a little calculus:
$$ \begin{align} \bar{x} &= \frac{1}{b - a} \int_a^b x \, dx \\ \\ &= \frac{1}{b - a} \frac{x^2}{2} \bigg|_a^b \\ \\ &= \frac{1}{2(b - a)} (b^2 - a^2) \\ \\ &= \frac{1}{2(b - a)} (b - a)(b + a) = \bf \frac{b + a}{2} \end{align}$$
That's just what we'd expect: add the high and the low and divide by two.
The variance of a discrete distribution is
$$\sigma^2 = \frac{1}{N} \sum_{i = 1}^N (x_i - \bar{x})^2$$
For our continuous distribution, we integrate that definition on the interval [a, b]:
$$ \begin{align} \sigma^2 &= \frac{1}{b - a} \int_a^b (x - \bar{x})^2 \, dx \\ \\ &= \frac{1}{b - a} \int_a^b \left[ x - \frac{a + b}{2} \right]^2 \, dx \\ \\ &= \frac{1}{b - a} \int_a^b \left[ x^2 - 2x \left( \frac{a + b}{2} \right) + \frac{(a + b)^2}{4} \right] \, dx \\ \\ &= \frac{1}{b - a} \left[ \frac{x^3}{3} - x^2 \left( \frac{a + b}{2} \right) + \frac{(a + b)^2 x}{4} \right]_a^b \\ \\ &= \frac{1}{b - a} \left[ \frac{b^3 - a^3}{3} + (a + b)\left( \frac{a^2}{2} - \frac{b^2}{2} \right) + \frac{(a + b)^2}{2} (b - a) \right] \\ \\ &= \frac{b^2 + ab + a^2}{3} - \frac{a^2 + 2ab + b^2}{2} + \frac{a^2 + 2ab + b^2}{4} \\ \\ &= 4b^2 + 4ab + 4a^2 - 6a^2 - 12ab - 6b^2 + 3a^2 + 6ab + 3b^2 \\ \\ &= \frac{b^2 - 2ab + a^2}{12} = \bf \frac{(b - a)^2}{12} \end{align}$$
Let's say we have a shoe store that sells pairs of shoes with a uniform probability of a sale throughout a seven-day week. That is, it's equally probable that a pair of shoes is sold on Monday as on Tuesday. The minimum number of pairs sold per week is 50, and the max is 250. Calculuate the probability of selling between 100 and 150 pairs of shoes. Calculate the mean and standard deviation, $\sigma = \sqrt{\sigma^2}$ of the distribution.
$$P_{100-150} = (150 - 50) \cdot \frac{1}{250 - 50} = \frac{100}{200} = \frac{1}{2}$$
The mean of the distribution is
$$\bar{x} = \frac{a + b}{2} = \frac{50 + 250}{2} = 150 \; \text{pairs}$$
Finally the variance is
$$ \begin{align} \sigma^2 &= \frac{(b - a)^2}{12} \\ \\ &= \frac{(250 - 50)^2}{12} = 3,333 \\ \\ &\text{so }\; \sigma = \sqrt{3333} = 58. \end{align}$$
The mean is $150 ± 58 \text{ pairs}$
The Bernoulli* distribution is suitable for modeling probability experiments that ask yes-or-no questions. For example, the flipping of a coin is a binary problem. The coin either comes up heads or it does not, where "not heads" is "tails."
We might write the probability of tossing heads as H, then the probability of tails is !H, which we read as "not H," or "not heads." Further,
$$H + !H = 1.$$
The Bernoulli distribution need not represent 50/50 probabilities. It could also be used to model the behavior of a non-fair coin like one that came up heads 75% of the time.
If we let the yes-event = 1 and the no event = 0, the average value of the Bernoulli distribution is
$$\bar{x} = 1(0.75) + 0(0.25) = 0.75$$
*
The curve under the bar graph above has a familiar "bell" shape. It's often referred to as a bell curve, but more often as the normal distribution or the Gaussian distribution, after Carl Friedrich Gauss.
The curve is a probability distribution. You can always read its meaning by imagining that the vertical axis is a measure of the relative probability or likelihood of something happening and that all of the somethings are arrayed in order along the x-axis.
The Gaussian curve is aways symmetric on either side of its maximum, and the maximum is the mean or average value. Whatever value or event is in the middle is the most likely. That "event" in our women's height example would be the "event" of being 5'-4" tall. Out in the "wings," probability is the lowest: There are far fewer very short and very tall women, and the probability of being short or tall is lower than being of more average height.
If we add up all of the probability under a Gaussian curve, we should get one (or 100%), the probability that something — anything at all — happened. Often we scale a Gaussian curve so that its total area – the area under the curve – is one. That's called "normalizing" the distribution.
Here's another example before we move on. The graph below shows the results of 5000 simulated throws of two dice. The sum of both dice is shown. Notice that because there are more ways to come up with a total of 7 (6+1, 5+2, 4+3),it's the most probable throw. After 5000 throws, the dice-total distribution looks pretty "normal."
Notice that in this example, we're not graphing probability but number of occurrences of a total, but the two should have the same shape. The sum of the heights of the green bars should be 5000, the total number of throws. Likewise, throwing a 2 or a 12 is less likely than throwing a 7.
We could normalize this distribution by dividing each value column value by the sum of all columns. This would give us the percent chance (if we multiplied by 100) of each throw, and it would sale the graph but maintain its shape. In the graph below, the green bars are the normalized simulated curve, and the purple bars are the exact expectations (see law of large numbers) we'd expect for a very large number of throws.
That's a tricky question. It comes from modeling random chance, but the functional form of the curve has to be derived using calculus. In particular, it is derived using the second fundamental theorem of calculus. We don't need to go there just yet, though; the result will serve our needs just fine. Here's what the Guassian function / Normal function looks like, with some explanation of its parameters.
This function might look complicated, but think of the first part as a constant prefactor. Then the exponential function is a symmetric bell-shaped curve that's translated by -h units along the x-axis and scaled by the 2σ2 in the denominator.
The
The example below might help. Imagine that you and a friend are throwing darts – aiming for the center. Your friend throws 12 darts in the pattern on the left. That's not so good, and the purple distribution reflects it. The distribution is wide, reflecting that many of the darts stuck relatively far from the center.
Now it's your turn. You throw darts much better and you throw the spread on the right, with most darts much closer to the center. If we were to graph the result of a great many of your throws (law of large numbers), we'd obtain the green Gaussian curve. That curve is much narrower, reflecting the fact that most shots are closer to the bullseye, with only a small number far away.
The width of a distribution is proportional to the precision of what it represents. The dart spread on the right is clustered closer together, therefore its precision is higher – and its distribution curve is narrower.
When it comes to data, the narrower the distribution, the better the quality of the data. A narrow distribution means more data closer to the mean, or more precise data. Remember, however, that precision and accuracy are different. It is possible to have a nice narrow distribution that is centered in the wrong place because of some other error.
Sigma is called the standard error or the standard deviation of a data set or the distribution that underlies it. It is a specific measure of the width of a distribution which is, once again, mathematically defined using calculus. Still, it's not hard to understand what the result means.
Take a look at the figure below. If we calculate the mean of data that conforms to a Gaussian distribution, then that calculated mean plus or minus σ (x ± σ) will comprise 68% of the total area under the distribution. That means 68% of the total probability or 68% of the data, depending on which we're talking about.
Take a look at the graph below. It shows a Gaussian distribution with x ± σ, x ± 2σ and x ± 3σ marked out.
It's worth remembering those numbers: ±σ captures about 68% of the total data set or distribution, and ±2σ and ±3σ capture about 95% and 98.5%, respectively.
Well, so far, σ is just an abstraction – just some lines and colors on a graph. We need to figure out how to calculate it for any set of data. Let's go . . .
The formula for calculating σ from a set of N values in a data set is:
Notice first that we're actually calculating σ2, and not just σ – we'll get to that later. The set of { xi } is our data, and the x is the mean of all N points of the data.
Now let's think about how that formula works. when we subtract x from xi, we're getting the "distance" of each point from the mean. We're squaring those differences to make them all positive, and then we're summing those up and dividing by their number N- i.e. averaging them.
That means that σ2 is the mean of the squares of the distances of each data point from the center of the distribution (which we assume to be the mean of the data).
Now σ2 is called the variance. We find the standard deviation of the data simply by taking a square root.
The
The
The
The
The
The
The
The
The data (50 values) was entered into the sheet in the blue column, and those data were averaged at the bottom of the column using the built-in AVERAGE() function of the program (I used NeoOffice Calc).
Then, in columns C and D, the difference between each data point and the mean, and its square, were calculated. The sum of the differences-squared was found in cell D53 using the built-in SUM() function.
In cell G3, the variance was calculated using the formula just to the right (normally these functions aren't displayed, I just showed it for your benefit). Notice that the MAX() function, which chooses the highest number from a group, allows us to put in fewer than 50 values and still do a proper calculation.
And finally we just take the square root of the variance in cell G5 to get sigma.
Now all of this could have been done just by applying the built in function STDEV() to the data in blue. The command would have been =STDEV(B3:B52), and would have yielded the same result. I wanted to go through it the long way – and you should, too – so that you could understand better what the formula does.
We would report this mean as 19.9 ± 2.5. This means that 68% (about two-thirds) of our data were within ±2.5 units of our mean, and it's a highly accepted way to report data and communicate to a reader that any mean has some associated error.
If you'd like to download this dataset and try to reproduce this calculation yourself (which I strongly encourage), just click below to get a .csv (comma-separated values) file that you can load into any spreadsheet program.
It's a small change and to be correct, we ought to use it. To get a feel for it, let's do a simple example.
Let's calculate the average and standard deviation (σ) of three test scores: 85%, 80% and 90%. The average is
(85 + 80 + 90) / 3 = 85
Now the variance (σ2) is
[(85-85)2 + (80-85)2 + (90-85)2]/3 = 16.7
and the standard deviation is the square root of the variance
σ = 4.1,
and that's fine – and it captures 68% of the underlying distribution as expected, if we can assume that it's normal. The trouble is that this is an awfully small sample, and we've assumed that these measurements contribute equally and independently to the calculation of σ – but they don't.
Take another look. In each of the squared terms of the σ calculation, we see the mean,
which contains contributions from all three of our measurements, 85, 80 and 90, so each of these terms depends, through the mean, on the other two. The data is not entirely independent in this calculation, but in dividing by N = 3 scores, we're treating it like it is.
Another way to think about it is that the data, at least when it comes to calculating σ, doesn't have as many degrees of freedom as we thought. There is some dependency of one measurement on the others. In this example, we've "used up" one of our degrees of freedom in the calculation of the mean, so we really only have 2 left, and in our calculation of σ, we really should divide by N-1 = 2 rather than N = 3.
It turns out that what we should really divide by when calculating σ2 is not N, per se, but N minus the number of pieces of data (also called degrees of freedom) that we've already used up in calculating other things – in this case the mean. It's kind of like needing n equations to find n unknowns.
For this reason, in simple calculations of σ, we usually modify our formula to
Notice that for very large data sets, the difference between N and N-1 is very small, and these two versions of σ converge – they get closer to each other.
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2016, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.
