Using calculus to learn more about the shapes of functions
In this section we'll learn how the tools of differential calculus (the first derivative in this section) can help us to learn much more about the graphs of functions than we could without them. Using the first derivative, we can determine just where maxima and minima of functions occur.
Adding the first derivative to our toolkit of curve sketching will be very valuable, but it's worth pausing here to emphasize this one thing about understanding the shape of a graph:
Old school!
There is no substitute for your basic pre-calculus skills when it comes to understanding the shape of the graph of a function. These skills include awareness of roots, asymptotes, holes, end behavior and symmetry. Don't forget them!
Maxima and minima of functions (extrema) – definitions
Before you move on, you should know this terminology — names of maxima and minima in the graph of a function:
- Global minimum — The global minimum is the lowest value of the function across its entire domain.
- Global maximum — The global maximum is the highest value of the function across its entire domain.
- Local minimum — a local minimum is the lowest value of a function in some local neighborhood, such as some defined interval [a, b].
- Local maximum — a local maximum is the highest value of a function in some local neighborhood.
The global or absolute maximum is the highest point on the graph of the function and the upper limit of its domain. The opposite is true for the global or absolute minimum.
A local max. or min. is just the highest or lowest point in an isolated region or "neighborhood."
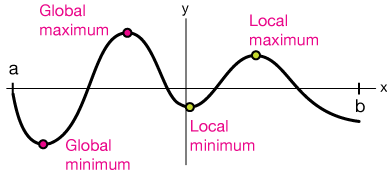
Note that if you're asked to find the maximum or minimum of a function on some closed interval like $[a, \; b]$, that max or min just might be one of the endpoints, so be sure to check those in your search.
The table below gives more mathematical definitions of the maxima and minima.
| Point | If $c$ is a number in the domain $[a, b]$ of the function $f$, then $f(c)$ is the: |
| Global minimum | on $[a, b]$ if $f(c) \le f(x)$ for all $x$ in $[a, b]$ |
| Global maximum | on $[a, b]$ if $f(c) \ge f(x)$ for all $x$ in $[a, b]$ |
| Local minimum | of $f$ if $f(c) \le f(x)$ when $x$ is near $c$ |
| Local maximum | of $f$ if $f(c) \ge f(x)$ when $x$ is near $c$ |
| End points | On a closed interval, [ ], make sure to test the endpoints of the interval when checking for maxima or minima. They might, in fact, be the highest or lowest points in that interval. |
Fermat's Theorem
To begin, let's recap an important theorem that was covered in the section on "existence theorems.", Fermat's theorem.
Fermat's theorem
If a function $f$ has a local minimum or maximum at a point $c$, and if $f'(c)$ exists, then $f'(c) = 0$.
Note: The fact that $f'(x) = 0$ does not necessarily mean that there is a local max. or min. at $c$. Fermat's theorem does not work in reverse. If there is a max. or min., then the derivative is zero. Existence of a zero derivative is not evidence of a max. or min.
One example of this caveat is the function $f(x) = x^3$, shown below. This function has no maxima or minima, but $f'(0) = 0$, so the slope of the function is zero at $x = 0$. This particular point is an inflection point.

Fermat's theorem says that if a function has a local maximum or minimum (which could be global), then the derivative at that point is zero. It's not to difficult to prove Fermat's theorem, so let's do it.
Proof
Referring to the definition of the local maximum above, we see that if a maximum value lies at $x = c$, then $f(x)$ must be larger than some other value of the function $f(x + h)$, where $h$ can be positive or negative. So:
$$f(c) \ge f(c + h)$$
which rearranges to:
$$f(c + h) - f(c) \le 0$$
We can divide both sides of this inequality by h to make this look like a derivative, then take the limit as $h \rightarrow 0^+$ from the right:
$$\lim_{h\to 0^+} \frac{f(c + h) - f(c)}{h} \le \lim_{h\to 0^+} (0)$$
Now we have assumed that $f'(c)$ exists, so the limit from the right must equal the limit in general:
$$\lim_{h\to 0^+} \; \frac{f(c + h) - f(c)}{h} \le 0$$
The expression on the left is $f'(c)$, so we have:
$$f'(c) \le 0$$
Now we could also do the same proof using the limit from the left, which would lead us to the inequality $f'(c) \ge 0$, and we'd have the double inequality,
$$0 \le f'(c) \le 0$$
The only way that both inequalities can be true is for $f'(c)$ to be equal to zero, so we have proved Fermat's theorem.
The derivative and slope
Remember that the derivative of a function gives its slope at any differentiable point in its domain.
The derivative of a rising function (positive slope) is positive, and
the derivative of a falling function (negative slope) is negative.
We proved this using the mean value theorem in another section. We can extend this thinking to understand that a function rises to left side of a maximum and falls off to the right, and a function falls to the left of the minimum and rises to its right. Of course, we have to be careful not to stray too far away from a max. or min. for that argument to hold. We generally speak of a "neighborhood" tight around the max. or min.


Critical points
Critical points of a function are points (possibly none or one) at which the first derivative of the function is zero.
As we saw in Fermat's theorem, a critical point might be a maximum or minimum of a function, or neither.
We'll eventually develop some ways to find out which, and to find out what a critical point might signify if it's not a max or min.
We find critical points simply by setting the first derivative equal to zero and solving for the roots: $f'(x) = 0$
Critical points
The critical points of a function are the zeros (or roots) of its first derivative.
Sometimes critical points are called critical numbers.
Example 1
Find the x-coordinates of the maxima and minima of $f(x) = -x^3 + 4x^2 + 4x - 16$
We begin by noting that this function can be factored by grouping:
$$ \begin{align} f(x) &= -x(x^2 - 4) + 4(x^2 - 4) \\[5pt] &= (4 - x)(x^2 - 4) \\[5pt] &= (4 - x)(x + 2)(x - 2) \end{align}$$
Real roots at x = 4, ±2
We can then sketch a quick graph with just the roots:

Now take the derivative of the function,
$$f'(x) = -3x^2 + 8x + 4$$
and set it equal to zero to find the critical points:
$$3x^2 + 8x + 4 = 0$$
Solving this quadratic equation by completing the square (or equivalently, using the quadratic formula, we get:
$$ \begin{align} 3x^2 + 8x + 4 &= 0 \\[5pt] x^2 - \frac{8}{3} x + \left( \frac{4}{3} \right)^2 &= \frac{16}{9} + \frac{12}{9} \\[5pt] \left( x - \frac{4}{3} \right)^2 &= \frac{28}{9} \\[5pt] x &= \frac{4 ± 2\sqrt{7}}{3} \end{align}$$
The two critical points are approximately x = -0.4 and x = 3.1, which match the minimum and maximum in our sketch, but now we know the x-coordinates exactly.
For a cubic equation, where we already know the end behavior and thus the order of the min. and max., we expect that critical points will correspond (for a positive leading coefficient) to the minimum on the left and the maximum on the right, both local.
We can confirm this, however by checking that for the minimum, the slope is negative on the left and positive on the right, and indeed, $f'(-2) \lt 0$ and $f'(1) \gt 0$. For the maximum, the slope on the left is positive, $f'(2) \gt 0$ and the slope on the right is negative, $f'(4) \lt 0$.
Here is the calculated graph of $f(x)$. Hopefully you can see that by augmenting your pre-calculus curve sketching skills with calculus, you can learn a little more about the graph of a function.
But at the same time, don't forget that you could already say a lot about this graph with just those pre-calculus skills.
In the next example, we'll use that to find the solution to an optimization problem that, until now, you could probably only have solved by estimation with a computer or calculator.

Why do I need to learn to sketch curves if I can always just graph them on a computer?

There is no guarantee that the person who programs a calculator or computer (e.g. enters the function or data) does so without error. My hope for you is that you can be the person in the room who says, "wait a minute ... that can't be right ... " People make mistakes (and always will), so don't trust blindly in what your computer or calculator says. Be in a position to check it out, maybe not in great detail, but at least qualitatively, by applying your most excellent curve sketching skills.
The first derivative test
Determining if a critical point is a max. or min.
The first derivative is used to find critical points, but we still need to test each one to determine if it's a maximum, a minimum, or neither (that's possible).
As we showed in the box above, the pattern of slopes for a maximum is
and for a minimum it is
We can use this simple test to check our critical points, one at a time, to see if each is a max, min, or neither. The idea is just to choose a convenient point on either side of a critical point, and evaluate the derivative at that point. We don't even really need the precise value of the derivative here, just to know whether it's positive or negative.
Here are a couple of examples of functions with critical points so we can see how the first-derivative test works.
Example 2
Find the critical points of $f(x) = x^3 - 3x + 1$ and determine whether each is a maximum or minimum (or neither) using the first-derivative test.
$$f'(x) = 3x^2 - 3$$
Now force the derivative to be equal to zero, and find the roots. These are the critical points:
$$ \begin{align} 3x^2 - 3 &= 0 \\[5pt] x^2 &= 1 \\[5pt] x &= ±1 \end{align}$$
The critical points are $x = ±1.$ Let's test them. First $x = -1.$ Set up a little grid like this. We'll choose points on either side of -1, say -2 and zero.

Now evaluate the derivative at our points and fill in the table. The values of the derivative at our test points are actually $f'(-2) = 9$ and $f'(0) = -3,$ but we just need the signs.

So our slopes go positive → 0 → negative, so this is a maximum.
Now we test the second critical point:

The slopes are negative → 0 → positive, so this is a minimum.
Notice that because we have the function, we can even calculate the precise locations of the max and min. The maximum value of the function is at (-1, f(-1)), or (-1, 3). The minimum is at (1, f(1)) or (1, -1). This is a big help in sketching the graph of a function like this, which doesn't have any rational roots.
Example 3
Find the critical points of $f(x) = e^{-x^2}$ and determine whether each is a maximum or minimum (or neither) using the first-derivative test.
$$f'(x) = -2x e^{-x^2} = - \frac{2x}{e^{x^2}}$$
Now forcing that derivative to be equal to zero, we get a single critical point at x = 0. We can test it at x = 1- and x = 1:

The slopes are positive → 0 → negative, so this is a maximum.
Here is a graph of that function so you can get the idea:

Example 4 – A rational function
Sketch a graph of $f(x)$ including the locations of any asymptotes. Use the first-derivative test to determine whether any critical points are maxima or minima.
$$f(x) = \frac{x^2 - 2x + 4}{x - 2}$$
First, let's take a look at the numerator. The zeros of the numerator are the zeros of a rational function. In this case, the discriminant is less than zero, so this function has no real roots.
$$ \begin{align} b^2 - 4ac &= (-2)^2 - 4(1)(-2) \\[5pt] &= 4 - 8 = -4 \end{align}$$
When the degree of the denominator is one greater than the degree of the numerator, the function has a linear slanted asymptote, the equation of which we can find by long division:
$$ \require{enclose} \begin{array}{rll} x\phantom{00000000} \\[-3pt] x - 2 \enclose{longdiv}{x^2 - 2x + 4}\kern-.2ex \\[-3pt] \underline{x^2 - 2x\phantom{000}} \\[-3pt] 4 \\[-3pt] \end{array}$$
The slanted asymptote is y = x. The denominator has a zero at x = 2, so there's a vertical asymptote there.
Now to find the critical point(s) by taking the first derivative. By the quotient rule, we start here:
$$f'(x) = \frac{(x - 2)(2x - 2) - (x^2 - 2x + 4)}{(x - 2)^2}$$
Expanding, we get:
$$f'(x) = \frac{2x^2 - 6x + 4 -x^2 + 2x - 4}{(x - 2)^2}$$
... which reduces to:
$$f'(x) = \frac{x(x - 4)}{(x - 2)^2}$$
The zeros of f'(x) are the zeros of the numerator above, x = 0 and x = 4, so those are candidates for maxima or minima.
Critical pts. at x = 0, x = 4
Now let's check the critical points using the first-derivative test. First x = 0. We'll choose x=-1 and x=1 for convenience,
$$f(-1) = \frac{5}{9} \phantom{000} \color{#E90F89}{\text{and}} \phantom{000} f(1) = -3,$$
So our first derivative test gives

Note that we don't actually need to calculate values of the derivative at x = -1 and x = 1, just to know whether their slopes are positive or negative. This speeds the first derivative test up a bit. According to the test, the critical point at x = 0 is a maximum. Now the second CP:

So the critical point at x = 4 is a minimum. It's not too difficult to calculate just where those critical points are on the graph:
$$ \begin{align} f(0) &= -2\\[5pt] f(4) &= 6 \end{align}$$
Finally, we can sketch a graph of our function:

The calculus we did is completely consistent with what we discovered about this function using only our algebra toolkit, and it extends that technique by allowing us to find the exact location of the relative maximum and minimum.
Understanding the graphs of a function and its derivative
Remember that the derivative gives the slope of a function at any point in its domain. Therefore when the slope of a function is negative, like the region between -∞ and -1 for $f(x)$, the graph of the derivative should lie below $y = 0$, which it does (red curve). Follow this trend across the graph, through all of its regions of negative and positive slope. Wherever the slope of $f(x)$ is increasing the graph of the derivative is positive; likewise for decreasing regions.
Next, sometimes the derivative graph passes through zero. That means $f(x)$ has zero slope at those points. Zero is the slope of a horizontal tangent, which occurs at extrema or critical points. We always have to be careful of exceptions, however. In fact, this function has a zero in its derivative at $x = 1$ with no corresponding maximum or minimum there.
We can use the first derivative to determine whether a particular extreme value is a maximum or a minimum:
- If the slope on the left side of an extreme value is negative and that on the right is positive, the extreme value is a minimum.
- If the slope on the left side of an extreme value is positive and that on the right is negative, the extreme value is a maximum.
On both sides of $x = 1$ the slope of $f(x)$ is negative except at $x = 1$, where it is zero. That means it can't be a maximum or a minimum (a case where the reverse of Fermat's theorem wouldn't work). The slope of the function must change sign on either side of a maximum or a minimum.
Practice problems
Find the critical points of each of these functions. Determine whether each is a minimum, a maximum or neither.
| 1. |
$f(x) = 3 - \frac{1}{4} x$ Solution$$f'(x) = -\frac{1}{4}$$ This derivative is constant, so it has no zeros. (-¼ is never equal to zero). So this function has no critical points, and therefore no maxima or minima. That make sense because $f(x)$ is a line with constant slope m = -¼ and y-intercept $y = 3$. |
| 2. |
$f(x) = sin(x) \phantom{000} 0 \le x \le \frac{3\pi}{2}$ Solution
|
| 3. |
$f(x) = \frac{x - 1}{x^2 - x + 1}$ Solution$$ \begin{align} f'(x) &= \frac{(x^2 - x + 1)(1) - (x - 1)(2x - 1)}{(x^2 - x + 1)^2} \\[5pt] &= \frac{x^2 - x + 1 - 2x^2 + x + 2x - 1}{(x^2 - x + 1)^2} \\[5pt] &= \frac{-x^2 + 2x}{(x^2 - x + 1)^2} \end{align}$$ Now the zeros of a fraction are the zeros of the denominator (because we could just multiply both sides by the denominator to get rid of it), so the critical points are $$ \begin{align} -x^2 + 2x &= 0 \\[5pt] x(2-x) &= 0 \\[5pt] x &= 0, \; 2 \: \color{#E90F89}{\longleftarrow \: \text{critical pts.}} \end{align}$$ Now check some convenient points on either side of these critical points to determine whether each is a maximum or minimum: $$ \begin{align} f'(-1) &\lt 0 \\[5pt] f'(0) &= 0 \color{#E90F89}{\leftarrow \: \text{minimum}} \\[5pt] f'(1) &\gt 0 \\[5pt] f'(2) &= 0 \color{#E90F89}{\leftarrow \: \text{maximum}} \\[5pt] f'(3) &\lt 0 \end{align}$$ Minimum: slope changes from negative to positive as we move from left to right across the critical point; Maximum: the opposite is true. |
| 4. |
$f(x) = x^{\frac{1}{4}} - x^{\frac{3}{4}}$ Solution$$f'(x) = \frac{1}{4} x^{-\frac{3}{4}} - \frac{3}{4} x^{-\frac{1}{4}}$$ Setting the derivative equal to zero and solving gives one critical point: $$ \begin{align} \frac{1}{4} x^{-3/4} - \frac{3}{4} x^{-1/4} &= 0 \\[5pt] x^{-3/4} &= -3 x^{-1/4} \\[5pt] x^{-3/4} &= 3x^{-1/4} \\[5pt] \frac{x^{1/4}}{x^{3/4}} &= 3 \\[5pt] \frac{1}{x^{1/2}} &= 3 \\[5pt] x^{1/2} &= \frac{1}{3} \\[5pt] x &= \frac{1}{9} \end{align}$$ Now test the point: $$ \begin{align} f' \left( \frac{1}{10} \right) &= 0.29 \gt 0 \\[5pt] f'\left( \frac{1}{9} \right) &= 0 \color{#E90F89}{\leftarrow \: \text{maximum}} \\[5pt] f' \left( \frac{2}{9} \right) &= -1.28 \lt 0 \end{align}$$ Here is a plot of the function showing its one maximum: |
| 5. |
$f(x) = 2x - tan(x) \: \text{ on } \: [0, 2\pi]$ Solution$$f'(x) = 2 - sec^2(x)$$ Now find the zeros (roots): $$ \begin{align} 2 - sec^2(x) &= 0 \\[5pt] sec^2(x) &= 2 \\[5pt] sec(x) &= ±\sqrt{2} \\[5pt] cos(x) &= ±\frac{\sqrt{2}}{2} \\[5pt] x &= \frac{\pi}{4}, \, \frac{3\pi}{4}, \, \frac{5\pi}{4}, \, \frac{7\pi}{4} \end{align}$$ There are an infinite number of solutions, but those are the four on the (arbitrary) interval [0, 2π] Here is a cosine graph just to help you find those critical points.
And here is a graph of the function showing the four solutions on this interval:
|
| 6. |
$f(x) = \sqrt{4 - x^2}$ Solution$$ \begin{align} f'(x) &= \frac{1}{2} (4 - x^2)^{-1/2}(-2x) \\[5pt] &= \frac{-x}{\sqrt{4 - x^2}} \end{align}$$ Now the derivative is only zero when x = 0, the one critical point. Now check the critical point: $$ \begin{align} f'(-1) &\gt 0 \\[5pt] f'(0) &= 0 \color{#E90F89}{\leftarrow \: \text{maximum}} \\[5pt] f'(1) &\lt 0 \end{align}$$
The graph is the top half of a circle of radius 2 with a maximum at x = 0. |
| 7. |
$-2x^3 + 54x + 5$ Solution$$f'(x) = -6x^2 + 54$$ Setting the derivative equal to zero gives two critical points: $$ \begin{align} 6x^2 &= 54 \\[5pt] x^2 &= 9 \\[5pt] x &= ±3 \end{align}$$ With polynomials, it's easy enough to do the 2nd derivative test to find out whether critical points are maxima or minima. $$ \begin{align} f''(x) &= -12x \\[5pt] f''(-3) &\gt 0 \: \text{so x = -3 is a minimum} \\[5pt] f''(3) &\lt 0, \: \text{ so x = 3 is a maximum} \end{align}$$ |
| 8. |
$f(x) = 3x^4 - 4x^3 - 12x^2 + 1$ Solution$$ \begin{align} f'(x) &= 12x^3 - 12x^2 - 24x \\[5pt] &= 12x (x^2 - x - 2) \\[5pt] &= 12x (x - 2)(x + 1) \end{align}$$ The zeros are $x = 0, -1, 2.$ We can use the second-derivative test to check these critical points: $$ \begin{align} f''(x) &= 36x^2 - 24x - 24 \\[5pt] f''(-1) &\gt 0, \: \text{so x = -3 is a minimum} \\[5pt] f''(0) &\lt 0, \: \text{so x = 0 is a maximum} \\[5pt] f''(2) &\gt 0, \: \text{so x = 2 is a minimum} \end{align}$$ |
discriminant
The discriminant of a quadratic function is the part of its solution by the quadratic formula that lies under the radical: b2 - 4ac. Because a square root is taken of this expression, it alone determines whether the roots of a quadratic function will be real or imaginary.
If b2 - 4ac > 0, the function has two real roots.
If b2 - 4ac < 0, the function has two imaginary roots which are complex conjugates of each other, e.g. 4 + 2i and 4 - 2i.
If b2 - 4ac = 0, then the function has one double root, and it is real.
neighborhood (math)
In math, the neighborhood of a point in a function is a set of other points of the function to which one could move along the graph and not leave it.

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.






