This section deals with linear momentum. Angular momentum (the momentum of turning or spinning objects) will be covered in another section.
In discussions about momentum and collisions, the concept of kinetic energy (KE) often comes up; the two are intertwined. You can still learn a lot about momentum without knowing anything about $KE$, but once you do learn that, you might want to revisit.
The change in momentum, $\Delta p$, is important in analyzing the forces involved in human-safety situations like car crashes. You can learn more about it on the impulse page.
Momentum vs. velocity
Momentum is mass × velocity. It's very easy to define, but why do we need it? Consider this:
Would you rather be hit in the face by a piano moving at 10 mi./hour or by a feather moving at the same speed?
Momentum links velocity to mass to give us a better gauge of how much energy a collision can deliver. Momentum is also a conserved quantity, meaning that the total momentum of every part of some system we can isolate, like a moving car, is always the same. We can use that fact to solve a lot of problems
For example, a cannon loaded with a cannonball can be our system, with momentum $p = 0$ because nothing is moving. The law of conservation of momentum tells us that this system must have a total momentum of zero until acted on by another force.
So if the cannonball does explode out of the cannon, in which case it will have some momentum, the cannon must "recoil" backward with the same momentum in the opposite direction, so that the two momenta (which are vectors) sum to zero. The speed of the cannon will of course be lower because of its greater mass.
The momentum of an object traveling in a straight line (linear momentum) is given the symbol $p$, and the definition $p = mv$. The letter $p$ comes from the latin word for momentum, petere. The SI units of momentum are mass (Kg) × velocity (m/s) =
$$Kg \cdot m \cdot s^{-2} \phantom{00} \text{or} \phantom{00} \frac{Kg \cdot m}{s^2}$$
Kinetic energy, $KE = \frac{1}{2} mv^2,$ is also a function of mass and velocity, but it is a scalar quantity, while momentum is a vector. We'll see that this makes momentum quite useful as a property of motion.
Momentum
Momentum is a vector
Momentum, $p = mv$ is mass (a scalar) multiplied by the velocity, a vector, therefore it too is a vector. Remember that multiplying a vector by a scalar can change its length and units, but not its direction.
The only things that matter about any vector are its length and direction. The length, or magnitude, of a momentum vector is how much momentum there is, and its direction is the direction of the momentum, or its velocity component.
Remember that vectors, like the two-dimensional ones on the right, can be moved around at will without loss of meaning, and that we add them head-to-tail, as shown here.
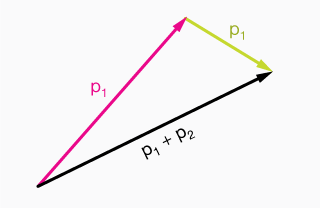
You can think of a momentum vector as a velocity vector multiplied by a scalar mass.
Pro tip:
Momentum is the singular form and momenta is the plural. We can calculate a single momentum, or several momenta.
Example 1
An apple falling 2 m from a tree reaches a speed of about 6 m/s just before hitting the ground. Calculate the momentum of the apple if its mass is 0.10 Kg.
$$ \begin{align} p &= (0.1 \, Kg) \left( 2 \, \frac{m}{s} \right) \\[5pt] &= 0.2 \, Kg \frac{m}{s} \end{align}$$
It's worth getting used to the units of momentum. Even when you forget formulas later on, if you learn the units, you'll have a good shot at reconstructing the formulas.
In this problem we worked only with the magnitude or size of the momentum, not its direction, as we often do with velocities.
Example 2
Which object has more momentum, a 2 Kg stone traveling at 85 mi./h or a 1 g pebble traveling at 170,000 mi./h ?
The momentum of the rock is
$$ \begin{align} p &= mv \\[5pt] &= 2 \, Kg \, (85 \, mi/h) \\[5pt] &= 170 \, Kg \frac{mi}{h} \end{align}$$
The momentum of the pebble (recall that 1 g = 0.001 Kg) is
$$ \begin{align} p &= mv \\[5pt] &= 0.001 Kg \, (170,000 \, mi./h) \\[5pt] &= 170 \, Kg \frac{mi}{h} \end{align}$$
So the momenta are the same, but notice how much faster the pebble has to be going in order to have the same momentum as the larger stone. That's almost 10% of the speed of light!
Closed system
A closed system is a collection of objects for which we can monitor and track the momenta of all of the components. It can be as simple as a ball rolling down a ramp, or an exploding object, where we track the speed and direction of all of the exploded pieces.
The total amount of momentum in a system is always conserved. That is, momentum is never lost or gained in a closed system.
For example, consider the drawing of billiard balls below. The system would be the balls and the table. The white ball is hit with momentum $p$ into the stationary red balls, all packed together, touching, and initially at rest. We'll assume that the masses of all balls are the same, just to make things easy. Because they are not moving, the total momentum of all of the red balls is zero, therefore the momentum of the entire system is just the momentum of the white ball, which is moving.
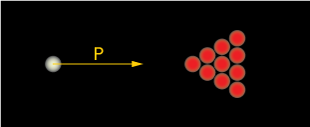
Shortly after the collision of the white ball with the lead red ball, the picture might look something like this (below). The white ball has lost most of its momentum, and each red ball has picked up a part of it. Each has scattered in a different direction, but the sum of the lengths of all 11 momentum vectors, $p_1, \; p_2, \; \dots \; p_{11}$, is equal to the length of the initial momentum vector $p$.

All of the momentum is still there after the collision, it's just been redistributed.
Here's another illustration of what conservation of momentum means in terms of vectors. Consider the pink ball with momentum $p_1$ as it simultaneously strikes the two green balls at rest ($p = 0$).
We denote the length of vector $p_1$ with absolute-value bars, | |. In the context of vectors, these always mean "length of."
Conservation of momentum says that $|p_1|$ before the collision must equal $|P_2|+|P_3|$ after it. We can never have more momentum in the green balls after the collision.
We might end up with less total momentum in the green balls, but that's because the energy of the collision can be distributed elsewhere, like sound or heat energy. In our ideal system,
$$|p_1| = |p_2| + |p_3|$$

Collisions
There are two basic types of collisions between objects, elastic collisions (also known as ideal collisions) and inelastic collisions.
Elastic collisions
In an elastic collision, both momentum and kinetic energy are conserved. You may not have learned about kinetic energy $(KE = \frac{1}{2} mv^2)$ yet, so we'll restrict our examples in this section to momentum only.
In an elastic collision, like the one illustrated below, two objects (the pink and green balls) approach each other with certain momenta. We'll assume, for simplicity, identical masses and identical velocities, except for direction, so the momenta are the same: $m_1v_1 = m_2v_2$.
In all collisions, momentum is conserved. That is, the total amount of momentum present in the system ($m_1v_1+m_2v_2$ here) is still present after the collision, except that it might be distributed a little differently.
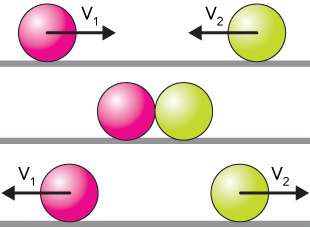
In this collision, the balls collide and instantaneously reverse direction to head the other way. In an elastic collision, there is no deformation of the objects, so there's no perturbation of the atoms and molecules within, so there's no heat radiated away.
Collisions of certain real objects, such as billiard balls, are very nearly elastic. The atoms and molecules of certain gases collide pretty much elastically, too, which is a big help in calculating the properties and behavior of them using the ideal gas law.
Inelastic collisions
In an inelastic collision, momentum is still conserved in just the way it was for an elastic collision, but kinetic energy is not. Consider the collision in the drawing:

The situation is the same, but now the balls may deform as they collide, which can, in turn heat them up through atomic and molecular motion. Sound or even heat and light might be given off, carrying energy away. This inelasticity is more common for a real collision. This energy is lost to the surroundings. While energy is always conserved in the universe, it is not conserved in this system; some is lost from the two balls to the surroundings.
Elastic & inelastic collisions
In an elastic collision, all kinetic energy remains with the colliding bodies.
In an inelastic collision, some kinetic energy is lost to the surroundings in other forms, such as heat and sound.
In a perfectly inelastic collision, two objects collide, stick together and move as one object thereafter.
Elastic collision with a massive object
Let's consider a ball rolling into an immovable object, like a wall. If we let the wall be very massive compared to the ball, then the collision won't cause it to move. The wall won't have any momentum, either before or after the collision.
We'll let capital letters $M$ & $V$ stand for the mass and velocity of the wall, and lower case, $m$, $v_1$ & $v_2$ stand for the mass and velocity of the ball.

The incoming velocity of the ball is $v_1$, and the outgoing velocity is $v_2$. Our job here is to find $v_2$ in terms of $v_1$.
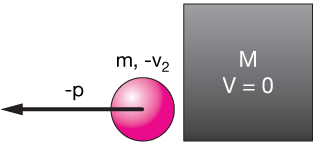
We begin with the total momentum of the system, before and after. Remember that these must be equal. Before the collision, the wall is stationary, so it has no momentum, so all of the momentum of the system is on the left side of this equation. On the right is the momentum after the collision. We'll allow for movement of the wall, then look at that later:
$$m v_1 = mv_2 + MV$$
If we divide both sides by $m$, we get
$$v_1 = v_2 + \frac{M}{m} V$$
Now let's put both velocities together on the left:
$$v_1 - v_2 = \frac{M}{m} V$$
Now we're going to want to compare this momentum-balance equation to the kinetic energy one, so let's square both sides and save this equation with a (1) for now:
$$(v_1 - v_2)^2 = \left( \frac{M}{m} \right)^2 V^2 \tag{1}$$
Now let's consider the kinetic energy of the system. It's the same process. The KE before the collision (left side of this equation) just involves the ball; the wall isn't moving. On the right, after the collision, we allow for movement of the wall.
$$\frac{1}{2} mv_1^2 = \frac{1}{2} mv_2^2 + \frac{1}{2} MV^2$$
If we multiply through by 2 we get
$$mv_1^2 = mv_2^2 + MV^2$$
and here again, we can divide by m:
$$v_1^2 = v_2^2 + \frac{M}{m} V^2$$
Moving $v_2^2$ to the left, we get:
$$v_1^2 - v_2^2 = \frac{M}{m} V^2$$
Now let's multiply both sides of that equation by $M/m$ so that we can line it up with equation (1) above.
$$\frac{M}{m} (v_1^2 - v_2^2) = \left( \frac{M}{m} \right)^2 V^2$$
Now we have two equations containing $(M/m)^2 V^2$, so we can hook those up using the transitive property:
$$\frac{M}{m} (v_1^2 - v_2^2) = (v_1 - v_2)^2$$
If we multiply both sides by $m/M$, we get
$$v_1^2 - v_2^2 = \frac{m}{M}(v_1 - v_2)^2$$
Now let's do something interesting. Let's ask what happens as we make the mass of the wall, $M$, infinitely large. The limit ("lim") notation below is used for that. This statement says, "in the limit where M becomes infinitely large, the expression goes to zero."
$$\lim_{M \to \infty} \, \frac{m}{M} (v_1 - v_2)^2 = 0$$
That is, as $M$ gets huge, $m/M$ gets very small, and the term on the right side of our equation vanishes, so we have
$$v_1^2 - v_2^2 = 0$$
That gives us
$$v_1^2 = v_2^2$$
If we take the square root of both sides we have
$$v_1 = ± v_2$$
Now we know that the ball isn't going through the wall, so $v_1 = -v_2$.
This means that in a collision of a moving object with an immovable object, all of the momentum remains in the moving object and its velocity is just reversed.
The scenario is just a bit more complicated if the ball hits the wall at a non 90˚ angle, of course, but not much more complicated. We'll tackle that later.
Of course, this is only true for an elastic collision, where all of the kinetic energy is conserved. In a real collision, we always lose some energy to the generation of sound or heat.
Example 3
Consider the setup below. If we can contrive a way to place a small explosive between two balls of equal mass at the center of a track, with bumpers on the ends to ensure as close as possible to elastic collisions, the two balls should bounce off either end with the same momentum, meet back in the middle and stop there. You can click the forward button to see an animation in slow motion.
This experiment (and it can be done as an experiment on an air-track, a track with very little dynamic friction) is a very good one for investigating conservation of momentum.
Think about it for a minute. At the beginning, the momentum of the system is zero. The law of conservation of momentum tells us that the momentum of the system must remain zero. Therefore the velocity of each ball after the explosion between them must be the same, but in opposite directions (vector velocities add to zero). After the bounce, the two balls collide with equal momenta but opposite direction, so the momenta add to zero and everything stops.
At all times in the animation, $p_{pink} = -p_{green}.$

Fireworks
Fireworks are a great example of conservation of momentum. The symmetry of fireworks explosions shows that momentum is conserved.
To achieve a pattern like this one, the explosion of the colored fireworks charges is timed so that it occurs right at the top of the flight of the fireworks package, where the velocity of the shell is zero. At that point the momentum of the system is roughly zero, so the explosion has spherical symmetry, in which all of the 3-D momentum vectors must add to zero.
That means there must be as many colored streaks to the right as to the left, as many up as down, and so on.
Example 4
In the early days of rocketry, many believed that a rocket couldn't move in space because there was nothing for the rocket exhaust to "push against" in the vacuum of space. But conservation of momentum won out, and it turns out that rockets do just fine with nothing to push against.
Consider the picture below. The top figure shows a stationary rocket. The velocity of the rocket is zero, so its momentum is zero. No hot gas molecules are being ejected from the nozzle at the back, so there is no momentum there.
Now let's ignite the fuel, which causes the ejection of hot gas molecules to the left at very high velocities.
While the momentum of each molecule or atom is very small, there are a very great number of them, adding up to the left-pushing momentum
$$p_{\text{engine}} = mv_1 + mv^2 + mv_3 + \dots$$
Now conservation of momentum says that the total momentum of this system (rocket plus gases) must remain zero, so there must be an equal momentum of the rocket toward the right, with
$$p_{\text{rocket}} = -p_{\text{engine}}$$
Here's an interesting thing: when it comes to real rockets, notice that as the fuel is ejected from the engine, the mass of the rocket actually decreases, so its velocity must increase proportionally in order to maintain the momentum. So as the fuel tank empties, the forward speed of the rocket increases even more.

Example 5: Perfectly inelastic collisions—coupling
In a perfectly inelastic collision, two objects collide along a line and they stick together, effectively forming one object. The classic example of this is the coupling of two train cars, like this:
In the animation (play it a few times), you can see that each train car has its own momentum, $p_1=m_1v_1$ and $p_2=m_2v_2$. The initial velocity of the second car is zero, so its momentum is zero. That means that all of the momentum of the system is in the first car.
After the collision, when the cars couple, they are effectively a single car with mass $k_1+m_2$, and a new velocity. That velocity has to be smaller than $v_1$ because the total momentum is conserved but the mass of the moving object has increased.
Kinetic energy in terms of momentum
Let's pause here to derive a new way to define kinetic energy, in terms of momentum. We already have $KE = \frac{1}{2}mv^2.$ We'll begin with the definition of momentum:
$$p = mv$$
Now square both sides to get
$$p^2 = m^2 v^2$$
The right side is looking like $\frac{1}{2} mv^2$, so let's divide out one of the masses:
$$\frac{p^2}{m} = mv^2$$
And finally, if we divide both sides by 2, we have:
$$\frac{p^2}{2 m} = \frac{1}{2} mv^2$$
So we have a new formula for the kinetic energy, on that comes in handy from time to time:
$$KE = \frac{p^2}{2m}$$
Two formulas for the kinetic energy
The kinetic energy of a moving object can be calculated in two ways:
$$KE = \frac{1}{2} mv^2 \phantom{000} \color{#E90F89}{\text{or}} \phantom{000} KE = \frac{p^2}{2m}$$
Example 6
Bumper cars at amusement parks bounce of one another in approximately elastic collisions. Let's say that a 130 Kg bumper car traveling at 10 m/s hits a 200 Kg bumper car moving at 13 m/s in the opposite direction. If the first car bounces back at a rate of 13.5 m/s, what must the velocity of the 2nd car be after the collision?

The velocity vectors and masses are shown. The green ball has a negative velocity. It doesn't matter which direction we choose as negative, just that they're opposite. We can calculate momentum vectors:
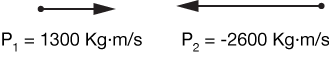
Now the total momentum is the sum of these oppositely-signed vectors:
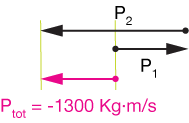
The law of conservation of momentum says that the momentum of this system must remain forever Ptot = -1300 Kg·m/s. We are given the momentum of the pink ball (cart) after the collision, $P_1 = (130 \, Kg)(-13.5 \, m/s) = -1755 \, Kg·m/s$:

These two momentum vectors must sum to the total system momentum. Plugging in $P_1 = -1755 \; Kg\cdot m/s and rearranging, we can find $P_2$:
$$ \begin{align} P_1 + P_2 &= -1300 \\[5pt] P_2 &= -1300 + 1755 \\[5pt] &= 455 \: \text{Kg m/s} \end{align}$$
Now $P_2 = m_2 v_2,$ so
$$m_2 v_2 = 455 \: \text{Kg·m/s}$$
from which we can solve for the velocity of the second cart.
$$ \begin{align} v_2 &= \frac{455 \: \text{Kg·m/s}}{200 \, Kg} \\[5pt] &= 2.28 \, m/s \end{align}$$
The second cart rolls away much more slowly, but that's necessary for momentum to be conserved. In reality, the collisions aren't completely elastic, and the post-collision velocities would be lower.
Example 7
A 100 Kg ball traveling at 10 m/s to the right collides head-on (i.e. in one dimension) with a 120 Kg ball traveling to the left at 5 m/s, as shown in the figure below. Calculate the post-collision velocities of the objects.

Momentum
The momenta of each ball are calculated like this:
$$ \begin{align} p_1 &= m_1v_1 = (100 \, Kg)(10 \, m/s) \\[5pt] &= 1000 \, Kg·m/s \\[5pt] p_2 &= m_2 v_2 = (120 \, Kg)(-5 \, m/s) \\[5pt] &= -600 \, Kg·m/s \end{align}$$
So the total momentum of the system before the collision (a vector sum) is
$$p_{total} = p_1 + p_2 = 400 \, Kg·m/s$$
That momentum must remain constant in this elastic collision.
Energy
The kinetic energy of the first ball is
$$ \begin{align} KE_1 &= \frac{1}{2}m_1 v_1^2 = \frac{1}{2}(100 \, Kg)(10 \, m/s)^2 \\[5pt] &= 5,000 \, J \end{align}$$
and the second ball:
$$ \begin{align} KE_2 &= \frac{1}{2}m_2 v_2^2 = \frac{1}{2}(120 \, Kg)(5 \, m/s)^2 \\[5pt] &= 1,500 \, J \end{align}$$
The total KE of the system is a sum of positive scalars:
$$KE_{total} = KE_1 + KE_2 = 6,500 \, J$$
Now after the collision, it must be true that the momenta will sum to 400 Kg·m/s. I'll write the mass values in from here on:
$$100 v_1 + 120 v_2 = 400 \, Kg \, m/s \tag{1}$$
And the total kinetic energy of this elastic collision must also remain the same, so we have:
$$\frac{1}{2} 100 v_1^2 + \frac{1}{2} 120 v_2^2 = 6,500 \, J$$
This we can reduce a bit to
$$50 v_1^2 + 60 v_2^2 = 6,500 \, J \tag{2}$$
Now we have two equations, (1) and (2), and two unknowns, the velocities $v_1$ and $v_2$. We can solve for $v_2$ in (1) and simplify to get
$$v_2 = \frac{400 - 100 v_1}{120} = \frac{20 - 5 v_1}{6} \tag{3}$$
Now we can plug that value of $v_2$ into (2):
$$50 \, v_1^2 + 60 \left( \frac{20 - 5 v_1}{6}\right)^2 = 6,500$$
To simplify and solve for $v_1$, let's first square that denominator and move it outside the parentheses:
$$50 \, v_1^2 + \frac{60}{36} (20 - 5 v_1)^2 = 6,500$$
That fraction reduced easily:
$$50 \, v_1^2 + \frac{5}{3} (20 - 5 v_1)^2 = 6,500$$
Now let's multiply through by 3/5 because the coefficients are divisible by 5 and it will clear the 5/3:
$$\frac{3}{5} \, 50 v_1^2 + (20 - 5 v_1)^2 = \frac{3}{5} 6,500$$
Multiplication gives:
$$30 \, v_1^2 + (20 - 5v_1)^2 = 3,900$$
Now expand the binomial ($20-5v_1)^2$:
$$30 \, v_1^2 + 25 \, v_1^2 - 200 v_1 + 400 = 3,900$$
Gathering terms gives a solvable quadratic:
$$55 \, v_1^2 - 200 \, v_1 = 3,500$$
We can reduce again by dividing by 5:
$$11 \, v_1^2 - 40 \, v_1 = 700$$
Now let's just complete the square to solve this exactly. Dividing by 11 gives:
$$v_1^2 - \frac{40}{11} v_1 = \frac{700}{11}$$
Adding the square of 1/2 the coefficient of $v_1$ to both sides, we get
$$v_1^2 - \frac{40}{11} v_1 + \left( \frac{20}{11} \right)^2 = \frac{700}{11} + \frac{400}{121}$$
Identifying the perfect square on the left and getting a common denominator on the right gives
$$\left(v_1 - \frac{20}{11} \right)^2 = \frac{7700 + 400}{121}$$
Almost there,
$$\left(v_1 - \frac{20}{11} \right)^2 = \frac{8100}{121}$$
Now we can take the square root of both sides and move the 20/11 to the right to isolate $v_1$ to find two possible solutions.
$$ \begin{align} v_1 &= \frac{20 ± 90}{11} = \frac{110}{11}, \, \frac{-70}{11} \\[5pt] &= 10 \, m/s, \: -6.36 \, m/s \end{align}$$
We'll rule out the first solution because it's physically impossible (see the diagram above!). So the final velocity of the pink ball (100 Kg) is -6.26 m/s. Plugging that into our earlier expression for $v_2$ gives:
$$v_2 = \frac{20 - 5 v_1}{6} = 8.63 \, m/s$$
Now let's use those velocities to check whether we do indeed end up with the same momentum as before the collision:
$$ \begin{align} p_1 &= m_1 v_1 + m_2 v_2 \\[5pt] &= (100)(-6.36) + (120)(8.36) \\[5pt] &= -636 + 1035.6 = 400 \, Kg\cdot m/s \end{align}$$
... and we do. The final picture looks like this:
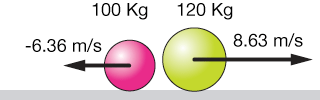
Whew! That's a lot of work, but very satisfying!
Example 8
Consider the diagram below. Two balls of equal mass but different velocities collide at the angle shown. If the final velocity of the green ball is 1.5 m/s and it is deflected by 105˚ to the right of its path (up in the figure), calculate the direction and speed of the pink ball after the collision.
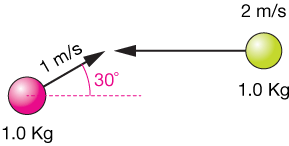
The first thing to do is to calculate the x- and y-components of the velocity vector of the pink-ball. We'll call the up and right directions positive and the down and left directions negative. It's not crucial which is which, just that we remain consistent throughout our work:

The x-component of the momentum is:
$$ \begin{align} p_{1x} = m_1 v_{1x} &= 1 \, Kg \cdot 0.866 \, m/s \\[5pt] &= 0.866 \, Kg\cdot m/s \end{align}$$
and the y-component of the momentum is:
$$ \begin{align} p_{1y} = m_1 v_{1y} &= 1 \, Kg \cdot 0.5 \, m/s \\[5pt] &= 0.5 \, Kg\cdot m/s \end{align}$$
(Yup, easy because of the 1Kg mass). The green ball has no vertical velocity, and therefore no vertical momentum, so its $x$- and $y$-momenta are
$$ \begin{align} P_{2x} = m_2 v_{2x} &= 1 \, Kg \cdot -2.0 \, m/s \\[5pt] &= -2.0 \, Kg\cdot m/s \end{align}$$
and
$$p_{2y} = 0$$
Now we can calculate the total momentum in the $x$- and $y$-directions:
$$ \begin{align} p_x = p_{1x} + p_{2x} &= 0.866 - 2.0 \\[5pt] &= -1.134 \, Kg\cdot m/s \end{align}$$
and
$$ \begin{align} p_y = p_{1y} + p_{2y} &= 0.5 + 0.0 \\[5pt] &= 0.5 Kg\cdot m/s \end{align}$$
The next step is to look at what we're given about what happens after the collision, keeping in mind that the total momentum in the x- and y-directions must remain constant. Here's the picture:
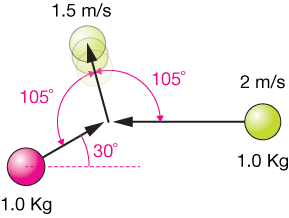
First we calculate the $x$- and $y$-components of the green ball velocity after the collision:

... and convert those to momenta by multiplying by the mass of the green ball:
$$ \begin{align} p_{2x} = m_2 v_{2x} &= 1 \, Kg\cdot 0.39 \, m/s \\[5pt] &= -0.39 \, Kg\cdot m/s \end{align}$$
and
$$ \begin{align} p_{2y} = m_2 v_{2y} &= 1 \, Kg \cdot 1.45 \, m/s \\[5pt] &= 1.45 \, Kg\cdot m/s \end{align}$$
Finally, the $x$- and $y$-momenta of both balls must sum to the total momentum in each of those directions before the collision (conservation of momentum), so we have:
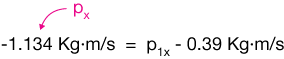
Rearrangement gives us the momentum of the pink ball in the $x$-direction:
$$P_{1x} = -1.134 + 0.39 = -0.744 \, Kg\cdot m/s$$
Likewise we can rearrange

to get:
$$P_{1y} = 0.5 - 1.45 = -0.95 \, Kg\cdot m/s$$
Now let's check everything for consistency. The total momentum in the $x$-direction after the collision is $p_{1x} + p_{2x} = -0.744 - 0.39 = -1.134 \, Kg\cdot m/s.$ The total momentum in the y-direction after the collision is $ p_{1y} + p_{2y} = 1.45 - 0.95 = 0.5 \, Kg\cdot m/s.$ These are the same $x$- and $y$-momenta as before the collision.
Here's a picture of the whole collision, drawn roughly to scale:
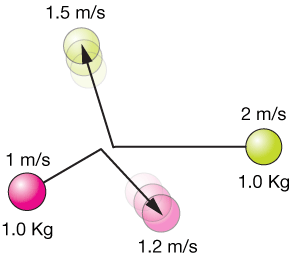
Example 9
Consider a low-speed coupling of two train cars. The car on the left collides with, then couples to the stationary car on the right. Caclulate the velocity of the coupled pair of cars after the collision, assuming no loss of velocity due to friction.

$$ \begin{align} p_1 &= m_1 v_1 = (30,000 \, Kg)(8 \, m/s)\\[5pt] &= 240,000 \, Kg \cdot m/s \end{align}$$
Now that's the momentum of the system after the collision, too.
The total mass of both cars together is $m_1 + m_2 = 60,000$ Kg, so the velocity of that double-car is calculated by rearranging the momentum formula,
$$p = mv \: \: \color{#E90F89}{\longrightarrow} \: \: v = \frac{p}{m}$$
and plugging in the numbers:
$$ \begin{align} v &= \frac{p}{m} = \frac{480,000 \, Kg\cdot m/s}{120,000 \, Kg} \\[5pt] &= 4 \, \frac{m}{s} \end{align}$$
If you think about it, it makes sense that the velocity is halved in this case.
Practice problems
-
Two balls of equal mass are on a level table. Ball 1 is moving with a velocity of v1 and ball 2 is stationary. After the collision, the velocity of ball 1 is zero. What can you conclude about the velocity of ball 2 after the collision?
Solution
The initial momentum of the system, which contains both balls, is $p = m v_1.$ After the collision, the total momentum is the same (it's conserved). Because the masses are the same, v2 after the collision must be equal to $v_1$ before the collision.
-
Calculate the momentum of a 1 metric ton (1000 Kg) crate moving down a ramp at a constant velocity of 1.5 m/s.
Solution
The momentum is $p = mv,$ so we have
$$p = (1000 \, Kg)(1.5 \, m/s) = 1500 \,Kg\cdot m/s$$
-
A superhero lifts a 2000 Kg vehicle, jumps straight into the air, and then throws the car horizontally at a speed of 25 m/s. If the mass of the superhero is 75 Kg, calculate the velocity at which she would be propelled in the opposite direction during the throw. (Of course, cartoons never portray her as moving backward).
Solution
The momentum of the car will be equal to the momentum of the superhero, just in the opposite direction. The momentum of the car is
$$ \begin{align} p = mv &= (2000 \, Kg)(25 \, m/s) \\[5pt] &= 5,000 \,Kg\cdot m/s \end{align}$$
Now the velocity of our superhero is
$$ \begin{align} v &= \frac{p}{m} = \frac{50,000 \,Kg\cdot m/s}{75 \, Kg} \\[5pt] &= 66.7 \,\frac{m}{s} = 149 \, \frac{mi}{h} \end{align}$$
-
How does doubling of the velocity of a moving object affect its momentum? How about its kinetic energy?
Solution
Momentum is $p = mv,$ so if we double the velocity we get $p_{\text{new}} = m(2v) = 2mv = 2p,$ so the momentum is doubled.
The kinetic energy, in terms of momentum, is $KE = \frac{p^2}{2m}.$ Mass being the same, if momentum doubles, then the KE quadruples from KE to 4KE.
$$ \begin{align} \text{Original} \phantom{000} KE &= \frac{p^2}{2m} \\[5pt] \text{double velocity} \phantom{000} KE &= \frac{(2p)^2}{2m} \\[5pt] &= 4 \, \frac{p^2}{2m} \end{align}$$
-
A grain "hopper" train car is rolling along a straight, level track at 0.5 m/s. The mass of the car is 28,000 Kg. If 10,000 Kg of grain is dumped in without any extra force on the car, what will its final velocity be after taking on the grain?
Solution
Our strategy is to find the momentum of the empty moving car, then assume that it doesn't change. We then use that momentum to calculate the new velocity using the combined mass.
$$ \begin{align} p &= mv \\[5pt] &= (28,000 \, Kg)(0.5 \, m/s) \\[5pt] &= 14,000 \, Kg\cdot m/s \end{align}$$
Now the velocity will be
$$v = \frac{p}{m} = \frac{14,000}{38,000} = 0.37 \, \frac{m}{s}$$
SI Units
SI stands for Le Système International d'Unités (French), or International System of Units.
It is a standardized system of physical units based on the meter (m), kilogram (Kg), second (s), ampere (A), Kelvin (K), candela (cd), and mole (mol), along with a set of prefixes to indicate multiplication or division by a power of ten.
Conservation
In science, to say that a quantity is conserved means that, in a closed system, or in the universe, the amount of that quantity never changes, though it might get spread around in different ways.
Scalar
A scalar is a number, which has no direction implied, like mass, temperature or speed. Velocity is a vector that has both speed and direction.

xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2016-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.