Predicting the equilibrium temperature
On this page we'll dive specifically into a kind of problem that is common in thermodynamics – calculating the equilibrium temperature reached after two substances at different temperatures are brought into contact or (in the case of liquids and gases) mixed.
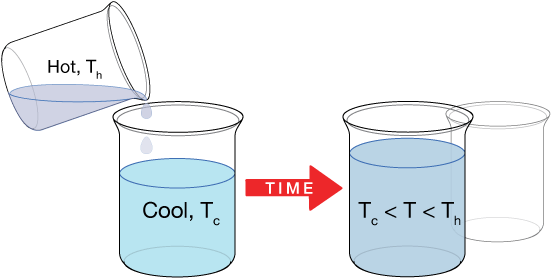
Two substances can be mixed or brought into thermal contact in any phase (liquid, solid, gas), and the equilibrium temperature will always be somewhere between the temperatures of the starting substances. We might, for example, ask questions like this:
- Two quantities of water, each at a different temperature, are mixed with no loss of heat to the surroundings. Calculate the equilibrium temperature of the mixture.
- Two metal objects, each at a different temperature and each wth a different specific heat, are brought into thermal contact, so that heat can flow between them. Calculate the equilibrium temperature.
The process always unfolds over time as shown in this graph:

The graph above shows temperature (T) vs. time (t). When hot and cold substances are brought into contact, heat flows from the hotter substance to the colder one. The temperature of the hot substance (Thot) drops and the temperature of the colder substance (Tcold) rises, until they meet at the equilibrium temperature, Teq. From the graph we can see the overall temperature change in each material, ΔThot and ΔTcold (green). The starred location where the temperature curve begins to stray from the equilibrium temperature reflects what happens in most real situations: some heat is inevitably exchanged with the surroundings and the temperature either moves upward or downward to establish a new equilibrium. In experiments, we'll always be concerned with Teq.
Now let's do some example calculations to see how this works.
Newton's law of cooling
Before we do an example, we ought to wonder why the red and blue curves in our graph above are curved. Newton's law of cooling tells us that the rate of heat transfer (which is actually the slope of those curves) is proportional to the difference in the two temperatures. Notice that at the beginning of the experiment (t = 0), the transfer is rapid, but it slows down as time goes on. This is always the way with heat transfer.
Example 1
100 mL of water at 80˚C is mixed with 500 mL of water at 19˚C. Calculate the equilibrium temperature of the mixture.
An adiabatic system is one in which no heat transfer between the system and the surroundings is possible. In practice, that generally means having a lot of insulation between the system (what's being studied) and its surroundings.
This means that
$$|q_{\text{lost by hot}}| = |q_{\text{gained by cold}}|,$$
where $q$ is heat, in Joules (J). The absolute-value signs are necessary because, by long-standing convention, heat lost by a system is negative and heat gained is positive.
Remember, also that 1 mL of water has a mass of 1 g (in fact, that's the definition of the gram), so 80 mL of water is 80 grams of water and so on. It's different for liquids of a different density.
In order to find the equilibrium temperature, we'll solve that equation, but here's some advice first: rearrange it equation like this:
$$ \begin{align} -q_{\text{lost by hot}} &= q_{\text{gained by cold}} \\[5pt] q_{\text{lost by hot}} &+ q_{\text{gained by cold}} = 0 \tag{1} \end{align}$$
Solving thermal equilibrium problems using equation (1) will be much more straightforward in terms of keeping track of negative signs, which can be tricky. Here's our setup:
$$ \require{cancel} \begin{align} q_{\text{lost by hot}} + q_{\text{gained by cold}} &= 0 \\[5pt] 100 \, \cancel{g} \left(4.184 \, \frac{J}{\cancel{g ˚C}} \right) (T_f - 80) \, \cancel{˚C} &+ \\[5pt] 500 \, \cancel{˚C} \left( 4.184 \frac{J}{\cancel{g ˚C}} \right) (T_f - 19) \, \cancel{˚C} &= 0 \\[5pt] \end{align}$$
After canceling our units, we can now multiply, distribute, group terms (do our usual good algebra moves) and solve for $T_f :$
$$ \begin{align} 418.4 (T_f - 80) + 2092 (T_f - 19) &= 0 \\[5pt] 418.4 T_f - 33472 + 2092 T_f - 39748 &= 0 \\[5pt] 2510 T_f - 73220 &= 0 \end{align}$$
$$ \begin{align} 2510 T_f &= 73220 \\[5pt] T_f &= 29.2 \, ˚C \end{align}$$
Does this make sense?
One last thing here: We should always ask whether our solution makes sense. Is it reasonable for 80 grams of hot water to only raise the temperature of 500 grams of 19˚C water by only ten degrees? That actually seems about right because the larger mass of water is 5× the smaller one. If the two masses were the same, we'd expect (because the specific heats are the same) that the equilibrium temperature would be the average of 80˚C and 19˚C, 49.5˚C.
Pro tip:
When solving for equilibrium temperatures, instead of solving $|q_{\text{lost by one substance}}| = |q_{\text{gained by the other}}|,$ it will be easier to keep track of signs if you solve $q_{\text{lost by one substance}} + q_{\text{gained by the other}} = 0.$
Then the only thing you'll have to keep track of is that $\Delta T = T_{final} - T_{initial}.$
Example 2: different substances
200 mL of cold (-19˚C) ethanol (C2H5OH, Cp = 2.46 J/g˚C, ρ = 0.789 g/mL) is added to 200 mL of liquid water (Cp = 4.184 J/g˚C) at 30˚C. Calculate the equilibrium temperature of the mixture.
First we need to use the density of ethanol to find its mass:
$$200 \cancel{mL} \left( \frac{0.789 \, g}{1 \, \cancel{mL}} \right) = 157.8 \, g$$
A density calculation like this is really just a unit conversion — no big deal. Now using our heat-change formula $q = m C_p \Delta T,$ we can set up our equilibrium equation, starting with the ethanol (I'll leave the units off this time for greater clarity):
Be careful here: 200 mL is only 200 grams for water. If you're doing these calculations for a different liquid substance, you'll need its density to calculate the mass from the volume before going on: volume × density = mass.
$$ \begin{align} 157.8 (2.46)(T_f - (-19)) \; &+ \\[4pt] 200 (4.184) (T_f - 30) &= 0\\[5pt] 388.19 (T_f + 19) + 836.8 (T_f - 30) &= 0 \\[5pt] 388.19 T_f + 7376 + 836.8 T_f - 25104 &= 0 \\[5pt] 1225 T_f - 17,728 &= 0 \end{align}$$
$$ \begin{align} 1225 T_f &= 17,728 \\[5pt] T_f &= 14.5 \, ˚C \end{align}$$
That makes sense. The volumes are similar, but the ethanol can't hold as much heat as the water, so the temperature should end up being closer to the temperature of the water.
Example 3: two metals
A 500 g block of titanium (Ti) at 650˚Cis brought into thermal contact with a 1.0 Kg (1000 g) block of aluminum (Al) at 25˚C. The specific heats of Ti and Al are CTi = 0.72 J/g˚C and CAl = 0.89 J/g˚C. Calculate the equilibrium temperature of the blocks once they reach it.

To set up our calculation, we state that the heat lost by the titanium plus the heat gained by the aluminum must be equal to zero. That's a statement of the law of conservation of energy. So we have:
$$ \begin{align} 500 \cancel{g} \left(0.72 \frac{J}{\cancel{g˚C}}\right) (T_f - 650) \cancel{˚C} \; &+ \\[4pt] 1000 \cancel{g} \left(0.89 \frac{J}{\cancel{g˚C}}\right) (T_f - 25) \cancel{˚C} &= 0 \\[5pt] 500(0.72)(T_f - 650) &+ \\[4pt] 1000(0.89)(T_f - 25) &= 0 \\[5pt] 360(T_f - 650) + 890(T_f - 25) &= 0 \\[5pt] 360 T_f - 234,000 + 890 T_f - 22,250 &= 0 \\[5pt] 1,250 T_f - 256,250 &= 0 \end{align}$$
$$ \begin{align} 1,250 T_f &= 256,250 \\[5pt] T_f &= 205 \, ˚C \end{align}$$
Example 4: a change of state
A 40 g cube of water ice (yes, "water" ice – there are all kinds of ice) at -20˚C is dropped into 200 mL of liquid water at 25˚C. Assume that all of the ice melts completely. Calculate the equilibrium temperature of the water. The specific heat of water ice is Cice = 2.05 J/g˚C and the enthalpy (latent heat) of fusion of water is Δ Hf = 333.55 J/g.
40g (cold ice to water above 0˚C
- Ice warms from -20˚C to 0˚C, its melting temperature;
- Ice undergoes a phase transition to liquid water, so the enthalpy of fusion, ΔHf will be required;
- Resulting water at 0˚C warms to the final temperature, TF, which is unknown.
The 200g of liquid water
- 200g of water at 25˚C cools to the same final temperature, TF, as above – the equilibrium temperature.
To help organize this work, it sometimes helps to map out what's going on using part of the water heating curve, below.

The red line shows the three parts of the heating process for the ice, and the blue one shows the change in the water temperature. The curves are not to scale. They meet at the equilibrium temperature, Tf.
Now adding all of these steps and setting the result equal to zero, according to the law of conservation of energy, will get us to our final temperature. Here's the initial equation, without units for simplicity and with the terms in the order presented in our list above:
$$ \begin{align} 40(2.05)(0 - (-20)) + 40(333.55) \; &+ \\[4pt] 40(4.184)(T_f - 0) + 200(4.184)(T_f - 25) &= 0 \end{align}$$
Now let's multiply, distribute, group like terms – just solid algebra moves – and solve for Tf.
$$ \begin{align} 82(20) + 13,342 + 167 T_f + 837(T_f - 25) &= 0 \\[5pt] 1,640 + 13,342 + 167 T_f + 837 T_f - 20,925 &= 0 \\[5pt] 1004 T_f + 5,943 &= 0 \\[5pt] 1004 T_f = 5,943 &\\[5pt] T_f = 5.9˚C & \end{align}$$
Does this make sense?
You might think this temperature is low in light of our previous examples, but recall that in melting, the ice extracts an extra 333 J/g of energy from the water without a change it its temperature. That represents an additional reduction of the water temperature that wasn't in those examples.
Example 5: a change of state?
A 50g cube of water ice at -20˚C is placed into 100 mL of water at 20˚C. Calculate the equilibrium temperature of the mixture.
$$ \begin{align} 50(2.05)(0 - (-20)) + 50(333.55) \; &+ \\[4pt] 50(4.184)(T_f - 0) + 100(4.184)(T_f - 20) &= 0 \end{align}$$
Now to solve for the final temperature:
$$ \begin{align} 102.5(20) + 16,678 + 209.2 T_f + 418.4(T_f - 20) &= 0 \\[5pt] 2,050 + 16,678 + 209.2 T_f + 418.4 T_f - 8,368 &= 0 \\[5pt] 627.6 T_f + 10,360 &= 0 \\[5pt] 627.6 T_f = -10,360 &\\[5pt] T_f = -16.5˚C & \end{align}$$
Does this make sense?
$$ \begin{align} q &= mC_p \Delta T \\[5pt] &= 100 \cancel{g} \left( 4.184 \frac{J}{\cancel{g˚C}} \right) (20 \cancel{˚C}) \\[5pt] &= 8,368 \, J \end{align}$$
Now compare that energy with the energy it takes just to melt a 50 g chunk of ice at 0˚C:
$$ \begin{align} q &= m \Delta H_f = 50 \cancel{g} \left( 333.55 \frac{J}{\cancel{g˚C}} \right) \\[5pt] &= 16,678 \, J \end{align}$$
So our water does not contain enough energy to melt the ice, and we'd expect to have a mixture of water and ice, coexisting at an equilibrium temperature of 0˚C, the melting temperature.
Practice problems
-
250 mL of water (density ρ = 1 g/mL, Cp = 4.184 J/g˚C) at 95˚C is added to 150 mL of ethanol (ρ = 0.789 J/g˚C) at -4˚C. The specific heat of ethanol is 2.46 J/g˚C. Calculate the equilibrium temperature of the mixture.
Solution
The data
$$ \begin{align} m_w &= 250 \, g \\[5pt] C_w &= 4.184 \, J/g˚C \\[5pt] T_{i,w} &= 95˚C \\[5pt] m_e &= 150 \cancel{mL} \left( \frac{0.789 \, g}{\cancel{mL}} \right) = 118.35 \, g \\[5pt] C_e &= 2.46 \, J/g˚C \\[5pt] T_{i,e} &= -4˚C \end{align}$$
The calculation
$$ \begin{align} 250(4.184)(T_f - 95) &+ \\[4pt] 118.35(2.46)(T_f - (-4)) &= 0 \\[5pt] 1,046(T_f - 95) + 291(T_f + 4) &= 0 \\[5pt] 1,337 T_f - 99,370 + 291 T_f + 1,164 &= 0 \\[5pt] 1,628 T_f - 98,206 &= 0 \end{align}$$
$$ \begin{align} 1,628 T_f &= 98,206 \\[5pt] T_f = \frac{98,206}{1,628} &= 60.3 ˚C \end{align}$$
-
A 205 g piece of brass at 120˚C is lowered into a 300 mL water bath at 22˚C. The specific heats of brass and water are Cbrass = 0.360 J/g˚C and CH2O = 4.184 J/g˚C, respectively. Calculate the temperature of the water once the system has come to equilibrium.
Solution
The data
$$ \begin{align} m_B &= 205 \, g \\[5pt] C_B &= 0.360 \, J/g˚C \\[5pt] T_{i,B} &= 120˚C \\[5pt] m_w &= 300 \, g \\[5pt] C_w &= 4.184 \, J/g˚C \\[5pt] T_{i,w} &= 22˚C \end{align}$$
The calculation
$$ \begin{align} 205(0.360)(T_f - 120) &+ \\[4pt] 300(4.184)(T_f - 22) &= 0 \\[5pt] 73.8(T_f - 120) + 1,255(T_f - 22) &= 0 \\[5pt] 73.8 T_f - 8,856 + 1,2551 T_f - 27,610 &= 0 \\[5pt] 1,329 T_f - 36,466 &= 0 \end{align}$$
$$ \begin{align} 1,329 T_f &= 36,466 \\[5pt] T_f = \frac{36,466}{1,329} &= 27.4 ˚C \end{align}$$
-
A bar of gold (Au) metal of mass 1.2 Kg and at 85˚C is placed in thermal contact with a 1.00 Kg block of platinum (Pt) at 900˚C. The specific heats of gold and platinum are CAu = 0.13 J/g˚C and CPt = 0.133 J/g˚C, respectively. Calculate the equilibrium temperature of the two bars of metal once heat has stopped flowing. Assume no loss of heat to the surroundings.
Solution
The data
$$ \begin{align} m_{Au} &= 1.2 \, Kg = 1,200 \, g \\[5pt] C_{Au} &= 0.13 \, J/g˚C \\[5pt] T_{i,Au} &= 85˚C \\[5pt] m_{Pt} &= 1.00 \, Kg = 1,000 \, g \\[5pt] C_{Pt} &= 0.133 \, J/g˚C \\[5pt] T_{i,Pt} &= 900˚C \end{align}$$
The calculation
$$ \begin{align} 1,200(0.13)(T_f - 85) &+ \\[4pt] 1,000(0.133)(T_f - 900) &= 0 \\[5pt] 156(T_f - 85) + 133(T_f - 900) &= 0 \\[5pt] 156 T_f - 13,260 + 133 T_f - 119,700 &= 0 \\[5pt] 289 T_f - 132,960 &= 0 \end{align}$$
$$ \begin{align} 289 T_f &= 132,960 \\[5pt] T_f = \frac{132,960}{289} &= 460 ˚C \end{align}$$
-
82 grams of gold metal (Cp = 0.13 J/g˚C) at 1200˚C is poured into an 800g steel mold which is at an initial temperature of 22˚C. The specific heat of steel is 0.466 J/g˚C and the enthalpy (latent heat) of fusion of gold is ΔHf = 67 J/g. The melting temperature of gold is 1064˚C. Calculate the equilibrium temperature of the gold. Will the gold solidify right away?
Solution
The data
$$ \begin{align} m_{Au} &= 82 \, g \\[5pt] C_{Au} &= 0.13 \, J/g˚C \\[5pt] T_{i,Au} &= 1,200˚C \\[5pt] m_{steel} &= 800 \, g \\[5pt] C_{steel} &= 0.466 \, J/g˚C \\[5pt] T_{i,steel} &= 22˚C \end{align}$$
The calculation
$$ \begin{align} 82(0.13)(T_f - 1200) &+ \\[4pt] 800(0.466)(T_f - 22) &= 0 \\[5pt] 10.66(T_f - 1200) + 372.8(T_f - 22) &= 0 \\[5pt] 10.66 T_f - 12,792 + 372.8 T_f - 8,201.6 &= 0 \\[5pt] 383.46 T_f - 132,960 &= 0 \end{align}$$
$$ \begin{align} 383.46 T_f &= 20,994 \\[5pt] T_f = \frac{20,994}{383.46} &= 54.7 ˚C \end{align}$$
-
An 25 g chunk of water ice at -18˚C is dropped into an insulated beaker containing 500 g of methanol at 19˚C. The specific heats of ice and water are Cice = 2.05 J/g˚C and Cmethanol = 2.53 J/g˚C, respectively. Calculate the equilibrium temperature of the mixture. Assume that all of the ice melts.
Solution
The data
$$ \begin{align} m_{ice} &= 25 \, g \\[5pt] C_{ice} &= 2.05 \, J/g˚C \\[5pt] T_{i,ice} &= -18˚C \\[5pt] m_{methanol} &= 500 \, g \\[5pt] C_{steel} &= 2.53 \, J/g˚C \\[5pt] T_{i,steel} &= 19˚C \end{align}$$
The calculation
$$ \begin{align} 25(2.05)(T_f -(-18)) &+ \\[4pt] 500(2.53)(T_f - 19) &= 0 \\[5pt] 51.25(T_f + 18) + 1265(T_f - 19) &= 0 \\[5pt] 51.25 T_f + 922.5 + 1265 T_f - 24,035 &= 0 \\[5pt] 1316 T_f - 23,112 &= 0 \end{align}$$
$$ \begin{align} 1316 T_f &= 23,112 \\[5pt] T_f = \frac{23,112}{1316} &= 17.6 ˚C \end{align}$$
Parse
To parse a question is to read it carefully and to organize the data within as to how it applies to the problem. This might include disregarding any data that's not meaningful to the problem at hand.
Density
Density is mass divided by volume. Its units are generally g/cm3 or Kg/m3. Recall that mass is not weight, but a measure of the amount of the substance. Denser substances (like lead) pack a lot of mass into a smaller volume, while less-dense substances (like feathers) need a larger volume to contain the same mass.

![]()
Dr. Cruzan's Math and Science Web by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2022-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.