The slope of a curve
At the heart of differential calculus is the idea of the slope of a curve. Until now you may have only thought about slopes of lines, but any curve can have a slope at a given point, provided that the curve is "well-behaved" at that point (more on that later).
The slope of a curve at some point in its domain is the slope of the line that is tangent to the curve at that point. Recall that a tangent is a line that just touches a curve at a single point, at least in the neighborhood of that point.
The slope of a curve at a point is the slope of the line tangent to the curve at that point.
One very important reason for finding the slope of a curve is that its value is zero (i.e. the tangent is horizontal) at a maximum or minimum of the function (see the figure). The tangent to a function is a horizontal line at a maximum or a minimum.
Among other things, this will allow us to find the exact solutions to optimization (most profit, least cost, least time, &c...) problems without estimating using a calculator.

Slope of a curve
The slope of a curve at a point is defined as the slope of the line tangent to the curve at that point.
The slope of a curve at a point (x,y) is the slope of the tangent to the curve at that point
Use the slider below the graph of
$$f(x) = x^3 - 6x^2 + 12x + 2$$
(just an average polynomial function, nothing special) to change the position of the tangent line along the curve. Pay attention to the slope of the line as you move it.
Notice that at the local maximum of $f(x)$, the value of the slope is zero. That will come in handy later for finding maxima and minima of functions, and for solving real problems such as maximizing profit or minimizing material used to perform some task.
When the function is rising (left to right, or as x increases), the slope of the tangent is positive, and when the function is falling then slope of the tangent is negative. On either side of the local maximum, the slope of the tangent line changes signs.
The derivative
The derivative of a function, $f(x)$ is another function, $f'(x)$ ("f-prime of x") that returns the slope of $f(x)$ at any point in its domain. This short section is a tour through the logic of finding the derivative. It's surprisingly simple (there is nothing essentially mysterious about calculus — don't worry).
There is nothing essentially mysterious about calculus.
Average slope
Let's say we want to find the average slope of the curve $f(x)$ between two points on its graph, $x_1$ and $x_2$. We simply draw a line between those points and calculate it's slope. We know how to calculate the slope of a line $(\Delta y / \Delta x)$; that's easy. It's customary to label the slope $m$. The graph below lays it all out.
Now of course m, as shown, is just the average value of the slope of $f(x)$ between $x_1$ and $x_2$, and it doesn't say anything about the details of the slope in between.
Could we find the value of the slope at just one of those intermediate points on the curve?

Slope at a point
This time we'll try to find the slope of our curve at some specific point $x$.
To do that, we'll first change our notation a little and use $x$ and $(x + \Delta x)$ instead of $x_1$ and $x_2$ to label our two points. This will allow us to reduce the width of the interval between them (the x-distance) by reducing $\Delta x$.
The slope of our secant line (

OK, almost there. Now do the following thought exercise: Imagine that $\Delta x$ gets smaller and smaller, and eventually vanishes or becomes "infinitessimally small." In the limit that $\Delta x = 0$, we would have the exact slope of our function at point $x$.
That is the essence of differential calculus: Finding the limit of a slope function as the change in the independent variable approaches zero. The graphs below will help you visualize how making the distance between our two points smaller gives us a better and better estimate of the slope of $f(x)$ at $x$. We'll wait for a while to actually prove that this limit is the slope of $f(x)$ at $x$.

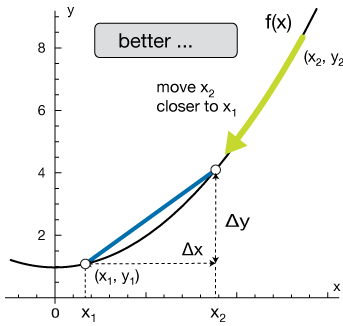
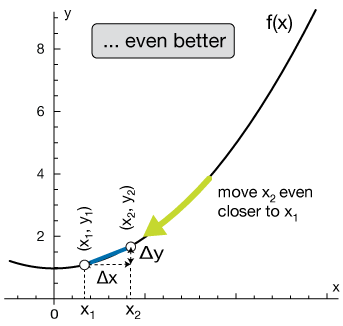
In the graphs above, our estimate of the slope of a function $f(x)$ at $x$ is just that – an estimate. In order to make it exact, we look at the slope,
$$m = \frac{f(x + \Delta x) - f(x)}{\Delta x}$$
If $\Delta x$ could be reduced to zero, then our slope would be exact. What we're talking about there is the limit of the slope function as $\Delta x$ → 0:
$$m = \lim_{\Delta x\to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}$$
The expression for m is often referred to as the difference quotient, and the limit of the difference quotient as $\Delta x$ → 0 is the derivative of the function at $x$.
You might have noticed that if $\Delta x$ goes to zero, the function "blows up," so this is a tricky limit. The thing to keep in mind is that $\Delta x$ is present in both the numerator and denominator of this limit; each is heading toward zero as $\Delta x$ → 0, and these "compete" in a way to give a finite limit. It's always that way with derivatives. You'll see how it works in the examples below.
Definition of the derivative
$$f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}$$
This expression is often referred to as the difference quotient.
... sometimes you'll see a slightly different notation: $\Delta x \, \longrightarrow \, h$
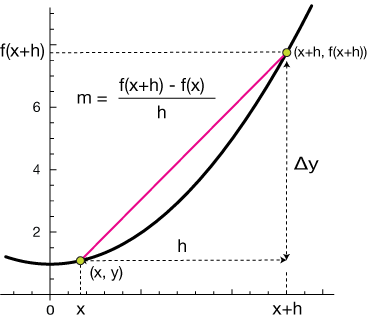
Finally, just a simple change of notation, replacing $\Delta x$ with $h$, simply to match most of the calculus textbooks you're likely to encounter.
Let's step through the logic again. Pick a point, $x$, on the smooth curve $f(x).$ Move some distance, $h,$ nbsp; away in the domain and choose a second point $(x+h, f(x+h)).$ Draw a secant line between the two.
Find the equation of the slope of that secant $(x, f(x))$ and $(x+h, f(x+h)).$
Find the limit of this slope function as $h \rightarrow 0.$ This will yield a function that gives the slope of $f(x)$ at any arbitrary point in its domain, provided that $f(x)$ has no discontinuities, like asymptotes, holes, sharp corners or the like. (More on these later).
Example 1
Find the derivative of $f(x) = x^2$
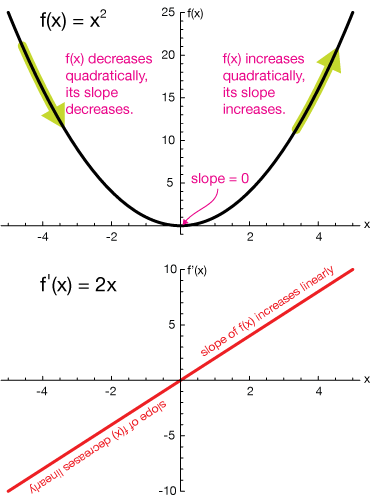
In preparation to use our new method to find the derivative of the simple quadratic function $f(x) = x^2$, let's take a look at the graph and think first about what we should expect from the derivative function we'll find.
When $x \lt 0$, any tangent to the curve will have a negative slope. For points close to zero, the steepness of those slopes approaches zero, and at $x = 0$, the global minimum of the function, the slope of the tangent is zero. Finally, for $x \gt 0$, the slope of the tangent to any point is positive.
Our derivative function will have to have those properties.

Now to find the derivative ...
First we write the definition of the derivative, the limit of the difference quotient. The notation $df/dx$ will be explained below. It is one of several ways to indicate a derivative.
$$\frac{df}{dx} = \lim_{h\to 0} \frac{f(x + h) - f(x)}{h}$$
Now plug the function in; $f(x+x)$, for example, is $(x+h)^2$.
$$= \lim_{h\to 0} \frac{(x + h)^2 - x^2}{h}$$
Expand the expression in the numerator and simplify. What generally happens in these limits is that the only terms to survive in the numerator all contain an h (or $\Delta x$), and that eliminates the possibility of a zero denominator:
$$= \lim_{h\to 0} \frac{x^2 + 2hx + h^2 - x^2}{h}$$
That gives us our derivative function:
$$= \lim_{h\to 0} \, (2x + h) = \bf 2x$$
Does this derivative make sense?
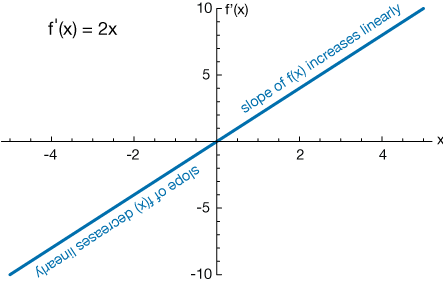
So we've found the derivative of $f(x) = x^2.$ It's $f'(x) = 2x,$ and it fits our criteria: It's negative when $x \lt 0$, it's positive when $x \gt 0$ and it's zero when $x = 0$.
Here are graphs of $f(x)$ (top) and its derivative.
Pro tip: Note that while sometimes you'll see the a function and its derivative plotted on the same axes, I'll avoid doing that. The two functions have different $y$-coordinates and should be plotted on separate axes.
The right side of $f(x)$ $(x \gt 0)$ has positive slope, and that slope is increasing as $x$ grows. The left side $(x \lt 0)$ has negative slope, with that slope increasing (but never becoming positive) as $x$ approaches zero. At the vertex, $x = 0$, the slope is zero.
All of these characteristics are reflected in $f'(x)$, which also shows that the increase in the slope of $f(x)$ in the upper right quadrant is linear. Likewise the increase in slope when $x \lt 0$ is also linear. Note that it's the change in slope that's linear, not the shape of the graph of $f(x)$ itself.
Derivative notation
There are a few ways of writing the derivative of a function. The first and last in this table are the most common. There are good reasons to know how to use both, as you will see later on in your study of calculus.
| $$\frac{df(x)}{dx} \; \text{ or } \; \frac{df}{dx}$$ | This notation was used by Leibniz, and it's one of the most useful. The ratio df/dx is pronounced "dee-f dee-x." |
| $$D_x f(x) \; \text{ or } \; D_x f$$ | This is Newton's notation and it isn't used that often. |
| $$f'(x)$$ | This shorthand for a derivative, "f-prime of x" is very handy and used a lot. |
Another formulation of the difference quotient
Finding the derivative at a point, a
This is a slightly different way to find the derivative of a function, this time at a single point in its domain, and you should be familiar with it. It's summarized in the graph →
We'd like to evaluate the slope of the curve $f(x)$ at the point $x = a$. The only difference here is that the distance $h$ is replaced by the difference between some coordinate $x$ and $x = a$, or $x - a$.
The slope is
$$m = \frac{f(x) - f(a)}{x - a}$$
and the difference quotient is:
$$f'(x) = \lim_{x\to a} \frac{f(x) - f(a)}{x - a}$$

Two variations of the difference quotient
You should be able to recognize either of these difference quotients as the derivative of a function. The one on the left is the general derivative $f'(x)$, and the other is the derivative of $f(x)$ at a specific point, $x = a$, or $f'(a)$.
$$f'(x) = \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h}$$
$$f'(x) = \lim_{x \rightarrow a} \frac{f(x) - f(a)}{x - a}$$
Applications of the derivative
The slope of a distance vs. time graph like this one (blue curve) is, by definition, the speed: speed = distance / time which is rise / run.
If we know the distance and time at any two points, it's easy to calculate the average speed, $\Delta x / \Delta t$ (green line). But average speed is quite different from instantaneous speed, the speed at any instant in time.
In the figure, the instantaneous speed is calculated at two different times, $t_1$ and $t_2$, as the derivative of $x(t)$ evaluated at $t_1$ and $t_2$.
Until now we haven't had a convenient way to arrive at instantaneous speeds. There are many more such derivative relationships in physics. Here are some of them:

Examples of derivatives used in physics


Example 2
The derivative of $f(x) = \frac{1 + x}{1 - x}$
This is an interesting function – a rational function. It has a vertical asymptote at $x = 1$, therefore finding the slope of $f(x)$ at $x = 1$ makes no sense – the function has no actual value there. The function (see graph below right) has a positive slope for all $x$ in its domain, except for $x = 0$, at which the slope is undefined. Here is the derivative expression for this function; it's just a matter of plugging the function into the difference quotient expression:
$$f'(x) = \lim_{\Delta x \to 0} \frac{\frac{1 + (x + \Delta x)}{1 - (x + \Delta x)} - \frac{1 + x}{1 - x}}{\Delta x}$$
Note: I'm switching back and forth between $\Delta x$ and $h$ notation on this page, I know. The meaning should be clear from the context of the problem, though. Get used to using both.
Now focus on what's above $\Delta x$ and make a common denominator:
$$= \lim_{\Delta x \to 0} \frac{\frac{(1 - x)(1 + x + \Delta x) - (1 + x)(1 - x - \Delta x)}{(1 - x)(1 - x - \Delta x)}}{\Delta x}$$
The $\Delta x$ in the denominator is just the full numerator multiplied by $\Delta x$; multiply and cancel terms in the numerator:
$$\lim_{\Delta x \to 0} \frac{1 + 2x + \Delta x - 2x - x^2 - x\Delta x - 1 + \Delta x + x^2 + x\Delta x}{\Delta x}$$
The $\Delta x$'s cancel:
$$\lim_{\Delta x\to 0} \frac{2 \Delta x}{\Delta x(1 - x)(1 - x - \Delta x)}$$
And the limit can be found directly by substitution of 0 for $\Delta x$:
$$= \lim_{\Delta x \to 0} \frac{2}{(1 - x)(1 - x - \Delta x)} = \frac{2}{(1 - x)^2}$$
Below are graphs of $f(x)$ and $f'(x)$. Notice that the slope of $f(x)$ is positive across its domain, and that the slope isn't defined at the vertical asymptote, $x = 0$ (because there's no value of the function at $x = 0$).
The graph of the derivative, $f'(x)$, reflects that by being positive everywhere. The derivative curve is also undefined at $x = 0$.

Example 3
The derivative of $f(x) = \frac{1}{x^2 + 1}$
We begin by writing this function into the difference quotient limit. In the first term of the numerator $x$ is $(x + h)$:
$$f'(x) = \lim_{h\to 0} \frac{\frac{10}{(x + h)^2 + 1} - \frac{10}{x^2 + 1}}{h}$$
Now we'll do two things. First, dividing by $h$ is the same as multiplying by the reciprocal; that's how the $h$ ends up in the denominator of the next step. Second, we'll get a common denominator and add those two fractions in the numerator:
$$= \lim_{h\to 0} \frac{10(x^2 + 1) - 10[(x + h)2 + 1]}{h(x^2 + 1)[(x + h)^2 + 1]}$$
Expanding the numerator a bit gives:
$$= \lim_{x\to 0} \frac{10x^2 + 10 - 10[x^2 + 2hx + h^2 + 1]}{h(x^2 + 1)[(x + h)^2 + 1]}$$
... and expanding all the way and cancelling where we can, including that $h$ in the denominator looks like this:
$$= \lim_{x\to 0} \frac{10x^2 + 10 - 10x^2 - 20hx - 10h^2 - 10}{h(x^2 + 1)[(x + h)^2 + 1]}$$
Now as $h \rightarrow 0$, two terms vanish:
$$= \lim{h\to 0} \frac{-20x - 10h}{(x^2 + 1)[(x + h)^2 + 1]}$$
Which gives us our derivative, f(x). Notice that we worked with this expression until taking the limit as $h \rightarrow 0$ would no longer cause a zero denominator. It always works that way with derivatives.
$$= \frac{-20x}{(x^2 + 1)(x^2 + 1)}$$
Our function $f(x)$ and its derivative $f'(x)$ are plotted below. It's tricky to interpret these graphs. You have to remember that the value of derivative (


Practice problems
Find the derivative of each of these functions using the difference quotient:
-
$f(x) = 7$
Solution
$$ \begin{align} f'(x) &= \lim_{h\to 0} \frac{f(x + h) - f(x)}{h} \\[5pt] &= \lim_{h\to 0} \frac{7 - 7}{h} = 0 \end{align}$$
This makes sense. $f(x)$ is a horizontal line with a constant slope of zero.
-
$f(x) = 2x^2$
Solution
$$ \begin{align} f'(x) &= \lim_{h\to 0} \frac{f(x + h) - f(x)}{h} \\[5pt] &= \lim_{h\to 0} \frac{2(x + h)^2 - 2x^2}{h} \\[5pt] &= \lim_{h\to 0} \frac{2(x^2 + 2xh + h^2) - 2x^2}{h} \\[5pt] &= \lim_{h\to 0} \frac{2x^2 + 4xh + 2h^2 - 2x^2}{h} \\[5pt] &= \lim_{h\to 0} \frac{4xh + 2h^2}{h} \\[5pt] &= \lim_{h\to 0} \frac{4x + 2h}{1} = \bf 4x \end{align}$$
Compare this to the derivative of f(x) = x2. It is the same, only four times as steep, which makes sense.
-
$f(x) = 3x^2 - 4$
Solution
$$ \begin{align} f'(x) &= \lim_{h\to 0} \frac{f(x + h) - f(x)}{h} \\[5pt] &= \lim_{h\to 0} \frac{3(x + h)^2 - 4 - (3x^2 - 4)}{h} \\[5pt] &= \lim_{h\to 0} \frac{3x^2 + 6xh + 3h^2 - 4 - 3x^2 + 4}{h} \\[5pt] &= \lim_{h\to 0} \frac{6xh + 3h^2}{h} \\[5pt] &= \lim_{h\to 0} \frac{6x + 3h}{1} = \bf 6x \end{align}$$
Notice that in $f(x) = 3x^2 - 4,$ the -4 is just a translation downward by 4 units, and can't affect the slope. This function must have the same derivative (slope) as $f(x) = 3x^2$ across its domain.
-
$f(x) = x$
Solution
$$ \begin{align} f'(x) &= \lim_{h\to 0} \frac{f(x + h) - f(x)}{h} \\[5pt] &= \lim_{h\to 0} \frac{(x + h) - x}{h} \\[5pt] &= \lim_{h\to 0} \frac{h}{h} = \bf 1 \end{align}$$
The line f(x) = x has a constant slope of 1, so this derivative makes sense.
-
$f(x) = x - 100$
Solution
$$ \begin{align} f'(x) &= \lim_{h\to 0} \frac{f(x + h) - f(x)}{h} \\[5pt] &= \lim_{h\to 0} \frac{(x + h) - 100 - (x - 100)}{h} \\[5pt] &= \lim_{h\to 0} \frac{x + h - 100 - x + 100}{h} \\[5pt] &= \lim_{h\to 0} \frac{h}{h} = \bf 1 \end{align}$$
The line f(x) = x has a constant slope of 1, and this is just that same line dropped vertically by 100 units, which doesn't affect its slope, so this derivative makes sense.
-
$f(x) = x^2 - 100$
Solution
$$ \begin{align} f'(x) &= \lim_{h\to 0} \frac{f(x + h) - f(x)}{h} \\[5pt] &= \lim_{h\to 0} \frac{(x + h)^2 - 100 - (x^2 - 100)}{h} \\[5pt] &= \lim_{h\to 0} \frac{x^2 + 2xh + h^2 - 100 -x^2 + 100}{h} \\[5pt] &= \lim_{h\to 0} \frac{2xh + h^2}{h} \\[5pt] &= \lim_{h\to 0} \frac{2x + h}{1} = \bf 2x \end{align}$$
Notice that this function has the same derivative as $f(x) = x^2.$ The -100 is just a translation down by 100 units, and doesn't affect the slope.
-
$f(x) = 3x^2 + x - 2$
Solution
$$ \begin{align} f'(x) &= \lim_{h\to 0} \frac{f(x + h) - f(x)}{h} \\[5pt] &= \lim_{h\to 0} \frac{3(x + h)^2 + (x + h) - 2 - (3x^2 + x - 2)}{h} \\[5pt] &= \lim_{h\to 0} \frac{3x^2 + 6xh + 3h^2 + x + h - 2 - 3x^2 -x + 2}{h} \\[5pt] &= \lim_{h\to 0} \frac{6xh + 3h^2 + h}{h} \\[5pt] &= \lim_{h\to 0} \frac{6x + 3h + 1}{1} = \bf 6x + 1 \end{align}$$
-
$f(x) = \frac{1}{x}$
Solution
$$ \begin{align} f'(x) &= \lim_{h\to 0} \frac{f(x + h) - f(x)}{h} \\[5pt] &= \lim_{h\to 0} \frac{\frac{1}{x + h} - \frac{1}{x}}{h} \; \leftarrow \; \text{Find common denom.}\\[5pt] &= \lim_{h\to 0} \frac{\frac{x - (x + h)}{x(x + h)}}{h} = \lim_{h\to 0} \frac{x - x - h}{xh(x + h)} \\[5pt] &= \lim_{h\to 0} \frac{x - x - h}{xh(x + h)} = \lim_{h\to 0} \frac{-h}{xh(x + h)}\\ [5pt] &= \lim_{h\to 0} \frac{-1}{x^2 + xh)} = \bf \frac{-1}{x^2} \end{align}$$
The key to this derivative was getting a common denominator for the terms in the numerator in the initial setup, then realizing that dividing by $h$ is the same as multiplying by 1/h.
Shortcuts to derivatives
If you did just the few problems above diligently, you may have noticed some patterns (besides that these can be long and tedious problems). Take a look again at each function and its derivative. These are derivatives of polynomial functions; the degree of the derivative is one less than that of the function. Also, the constant in the function is not in the derivative (though there may still be a constant term in the derivative).
There are a few simple rules and shortcuts you can take in figuring out derivatives that will make life much easier. The first is this rule
The derivative of a constant is zero.
The graph of the constant function, $f(x) = C,$ where $C$ is a number, is a horizontal line. The slope of such a line is zero.
So the derivative of any constant function, $f(x) = C,$ is zero. Easy peasy.
$$ \begin{matrix} f(x) = C && f'(x) = 0 \\[5pt] f(x) = 2 && f'(x) = 0 \\[5pt] f(x) = -7 && f'(x) = 0 \end{matrix}$$
The derivative of a constant is zero.
The derivative of a sum is a sum of derivatives
The sum rule of derivatives looks like this:
$$ \begin{align} \text{If } \; f(x) &= g(x) + h(x) + \dots + k(x), \text{ then} \\[5pt] \frac{df}{dx} &= \frac{dg}{dx} + \frac{dh}{dx} + \dots + \frac{dk}{dx} \end{align}$$
It can be derived using the limit difference quotient, writing a function that is a sum as:
$$ \begin{align} y &= f(x) = u(x) + v(x) + \dots, \text{ then} \\[5pt] (y + \Delta y) &= (u + \Delta u) + (v + \Delta v) + \dots , \\[5pt] \text{so } \; \Delta y &= \Delta u + \Delta v + \dots \end{align}$$
Then if we divide each term by $\Delta x$, we get the derivative on the left as a sum of derivatives on the right. It's easy to generalize to subtraction, which is just addition of the negative.
The derivative of a sum is the sum of derivatives.
The derivative of $x^n$ — The power rule
This is the real time saver. If you sit down and solve enough problems using the limit definition of the derivative we developed above, you'll see that it can be cumbersome and time-consuming.
If you work enough problems, you'll see a pattern. It's shown on the left, and it's something you should definitely memorize as soon as possible.
For $f(x) = Ax^n$, where $A$ and $n$ are numbers and $x$ is our variable, the derivative is $f'(x) = nAx^{n-1}$. We multiply the coefficient of the independent variable by the exponent, and drop the power of the exponent by one unit.
Pretty simple. Make sure to work through the examples here. Most students get the hang of using this algorithm pretty quickly.
The power rule
The power rule of differentiation is the single most powerful rule you'll use when finding derivatives of functions:
$$\text{If } f(x) = x^n \phantom{000} \text{then} \phantom{000} \frac{df}{dx} = n x^{n-1}$$
Proof of the power rule for integer exponents
To prove the power rule, we'll take advantage of the pattern we find in the expansion of a binomial $(a+b)$ taken to the $n^{th}$ power. We're dealing only with integer powers here, but in another section we'll expand this definition to include all real-number exponents.
The binomial expansion formula is:
$$(a + b)^n = \sum_{k = 0}^n \binom{n}{k} \, a^{n - k}b^k, \; \text{ where}$$
$$\binom{n}{k} = \frac{n!}{k!(n - k)!}$$
Narrow-screen divices
Scroll wide equations left ↔ right
The expansion of $(a + b)^n$ looks like this:
$$(a + b)^n = a^n + na^{n - 1}b + \frac{n(n - 1)}{2!} a^{n - 2} b^2 + \frac{n(n - 1)(n - 2)}{3!} \, a^{n - 3} b^3 + \dots + n ab^{n - 1} + b^n$$
Now we plug that into the difference quotient definition of the derivative:
$$\frac{df}{dx} = \lim_{h\to 0} \frac{(x + h)^n - x^n}{h}$$
$$\frac{df}{dx} = \lim_{h\to 0} \frac{ \left( x^n + nx^{n - 1} h + \frac{n(n - 1)}{2!} x^{n - 2} h^2 + \frac{n(n - 1)(n - 2)}{3!} x^{n - 3} h^3 + \dots + nxh^{n - 1} + h^n \right) - x^n}{h}$$
Now notice that the first and last terms, $x^n$, cancel to give us the following equation with only one term containing $h$ to the first power. The other terms contain $h$ raised to higher powers, and thus vanish in the limit as $h \rightarrow 0$.
$$\frac{df}{dx} = \lim_{h\to 0} \frac{nx^{n - 1} h + \frac{n(n - 1)}{2!} x^{n - 2} h^2 + \frac{n(n - 1)(n - 2)}{3!} x^{n - 3} h^3 + \dots + nxh^{n - 1} + h^n}{h}$$
Now each term of the denominator contains an $h$ but all contain higher powers of $h$ than 1 except for the first term, therefore when we divide each term by $h$ and take the limit as $h \rightarrow 0$, all terms but the first vanish, leaving
$$\frac{df}{dx} = n \, x^{n - 1}$$
Now the binomial expansion is only defined for integers, therefore this proof is only for integer exponents of $x$.
Practice problems
Find the derivative of each of these functions using the power rule:
-
$f(x) = 3x^2 - 5$
Solution
$$f'(x) = 6x$$
-
$f(x) = x^3 - 2x^2$
Solution
$$f'(x) = 3x^2 + 4x$$
-
$f(x) = x^2 - 2x$
Solution
$$f'(x) = 2x - 2$$
-
$f(x) = 2x^3 - x^2 + x + 3$
Solution
$$f'(x) = 6x^2 - 2x + 1$$
-
$f(x) = 3x + 7$
Solution
$$f'(x) = 3$$
-
$f(x) = -x^2 - 2x$
Solution
$$f'(x) = -2x - 2$$
-
$f(x) = x$
Solution
$$f'(x) = 1$$
-
$f(x) = -x^2 - x$
Solution
$$f'(x) = -2x - 1$$
Video examples
1. Simple derivatives using the difference quotient (1)
Differentiation (finding the derivative) of $f(x) = x^2$ using the difference quotient. Both the function and its derivative are plotted. Note: Sometimes I refer to a function that rises on the left as "increasing as $x \rightarrow \infty$". That's actually a negative slope. I'll try to reform.
Minutes of your life: 3:43
2. Simple derivatives using the difference quotient (2)
Differentiation of $f(x) = x^2 + 3$ using the difference quotient. What is the effect on the slope of adding a constant to a function ? Both the function and its derivative are plotted and we learn that that constant (3) doesn't affect the slope of the parabola at all, so the derivative isn't affected either.
Minutes of your life: 3:24
3. Simple derivatives using the difference quotient (3)
Here is another example of differentiating a function using the difference quotient approach. This time the function is $f(x) = x^3$.
Minutes of your life: 4:08
4. One more example of finding a derivative using the difference quotient (4)
This time we'll look at the derivative of the rational function $1/(x - 1)$.
Minutes of your life: 4:05
5. Finding derivatives using the power rule: If $f(x) = x^n$, then $f'(x) = n·x^{n-1}$
Here are six examples of taking derivatives using the power rule. The power rule is not derived here, just used, but we do talk a bit about the properties of derivatives.
Minutes of your life: 3:51

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.