Refraction of waves leads to many familiar phenomena
Refraction of light leads to many phenomena you've probably seen, and some that are very useful in science, technology, and sometimes art.
The basic idea is that light does not travel at the same speed in all transparent materials. For example, the speed of light in vacuum is
$$c = 2.99792458 \times 10^8 \, \frac{m}{s},$$
but it slows, for example, to 1.97 × 108 m/s in common window glass.
In diamond, the speed of light is about 1/3 of its speed in vacuum, and this in part leads to the sparkle and color of high-quality diamonds.
The essence of refraction is this speed difference in different materials. When light beams pass from one material to another, in which the speed of light is different, its path bends at the interface.
Refraction is responsible for the separation of colors in a prism, the mirage "lakes" you see at the end of a hot road in summer, the midday sky being blue and the morning and evening skies being orange and red.

We'll see how it all works in this section. First we'll define the index of refraction for convenience, then we'll use Snell's law to calculate refraction angles.
A derivation of Snell's law is given at the end of this section, but you'll need to know about differential calculus to follow it. Don't worry about it if you haven't studied calculus yet. Just use the law and come back to how it's derived later.
Interface
An interface is a line or surface that separates two types of material.
The surface between air and water is an interface. So is the surface between the oil and water when oil floats on top of water.
The index of refraction, n
The index of refraction (n) of any material is the ratio of the speed of light in vacuum, $c = 2.99792458 \times 10^8 \, m/s,$ to the speed of light in that material.
$$n = \frac{c}{v}$$
where v is the speed of light in the material. Notice that because we divide a velocity by a velocity here, the result is unitless.
The index of refraction, $n,$ is unitless.
Light travels its fastest in vacuum, and slows down in all other materials, so the index of refraction of materials is always a number greater than one. The larger the index of refraction, the smaller the speed of light in the material. In other words, n is inversely proportional to the speed of light in the particular material.
The table shows the speed of light and index of refraction for several transparent materials.
The index of refraction can be measured for materials that aren't transparent to visible light (opaque materials) by using high energy radiation that penetrates such materials, such as gamma rays.
Speed of light and index of refraction (n) in various transparent materials
| medium | speed (m/s) | n |
|---|---|---|
| vacuum | 2.9979 × 108 | 1.00 |
| air | 2.9970 × 108 | 1.0003 |
| water | 2.25 × 108 | 1.33 |
| ethanol | 2.20 × 108 | 1.36 |
| quartz | 2.0555 × 108 | 1.4585 |
| window glass | 1.97 × 108 | 1.52 |
| diamond | 1.24 × 108 | 2.42 |
Snell's law*
Snell's law allows us to relate the angle of incidence and the angle of refraction to the indices of refraction, $n_1$ and $n_2$.
The figure shows a beam of light entering water from air at an angle from the vertical. The figure shows that the angles of incidence ( $\theta_i$ ) and refraction ( $\theta_r$ ) are defined with respect to the normal to the interface. A normal is a line that is perpendicular to an interface from all angles with respect to the interface surface.
Snell's law is
$$n_1 \, \sin(\theta_1) = n_2 \, \sin(\theta_2)$$
We can rearrange Snell's law to solve for the angle of refraction, $\theta_2$, using some inverse trigonometry:
$$ \begin{align} n_1 \, \sin(\theta_1) &= n_2 \, \sin(\theta_2) \\[5pt] \frac{n_1 \, \sin(\theta_1)}{n_2} &= \sin(\theta_2) \\[5pt] \theta_2 &= \sin^{-1} \left( \frac{n_1 \, \sin(\theta_1)}{n_2} \right) \end{align}$$
Now if our beam of light passes from a medium with a higher speed of light (smaller $n$) into one with a lower speed (larger $n$), then $n_1/n_2 \le 1$. It's also true that $\theta \lt \pi/2$ because we won't have an angle of incidence greater than or equal to a right angle (beam skimming along the surface but not entering). Further, because the sine function between 0 and $\pi/2$ is an increasing function with a maximum of 1 at $\theta=\pi/2$, the sine of a larger angle is larger than the sine of a smaller angle. Rearranging Snell's law another way gives:
$$\frac{n_1}{n_2} \ \frac{\sin(\theta_2)}{\sin(\theta_1)}$$
This means that for light passing from a medium of low refractive index to a higher index, the angle with respect to the normal will decrease. The opposite must be true for light moving from a higher index to a lower one.
The diagram shows this situation for light passing from air to a liquid. The incident beam is measured from the normal to the interface, and the angle that the refracted beam makes with that same normal will be smaller.
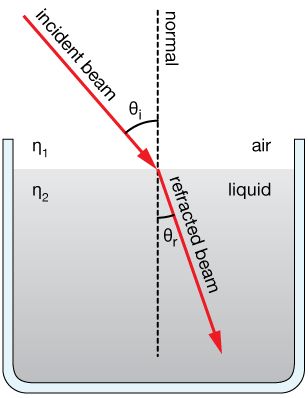
This situation can be reversed. If the beam originates in the liquid (larger $n$) and passes through to air, the angle made with the interface normal will increase. In the examples below we can get quantitative about it.
* Snell's law is derived using calculus at the bottom of the page.
Snell's law
When light passes through an interface separating two media in which the speed of light (and thus the index of refraction, $n$) is different, the angle of that light with respect to the normal to the interface will change according to Snell's law:
$$n_1 \, \sin(\theta_1) = n_2 \, \sin(\theta_2)$$
where $n_1$ and $n_2$ are the indices of refraction in medium 1 & 2, respectively, and $\theta_1$ & $\theta_2$ are the angle made by the beam of light and the normal to the interface between the two media.
Direction of refraction
When light enters a medium with a higher index of refraction, its angle with the normal to the interface will decrease.
When light enters a medium with a lower index of refraction, its angle with the normal to the interface will increase.
Example 1
A beam of light passes into a flat piece of glass at an angle of 50˚ with respect to the surface normal. Calculate the angle of the refracted beam inside the glass and after it passes through the other side back into air.
$$\theta_{r1} = \sin^{-1} \left( \frac{n_{air} \, \sin(\theta_{i1})}{n_{glass}} \right)$$
If we plug in $n_{\text{air}}=1.00$, $\theta_{i1}=50^{\circ}$ and $n_{glass}=1.52$ (from the table above), we get
$$\theta_{r1} = \sin^{-1} \left( \frac{1.00 \, \sin(50˚)}{1.52} \right)$$
and $\theta_{r1}$ is, as expected, less than 50˚:
$$\theta_{r1} = 30.3˚$$
Now to solve for the exit angle at the other interface, we have to draw a new surface normal (shown as "normal-2"). The angle of incidence with respet to that normal is just the angle of refraction of our first beam, 30.3˚, and we'll name it $\theta_{i2}$, the "second angle of incidence,\quot; just to keep things organized.
Snell's law gives us the formula for our exit angle:
$$\theta_{r2} = \sin^{-1} \left( \frac{n_{glass} \, \sin(\theta_{i2})}{n_{air}} \right)$$
Plugging in the numbers gives us an easy expression to calculate (make sure your calculator is set to degrees!)
$$\theta_{r2} = \sin^{-1} \left( \frac{1.53 \, \sin(30.3˚)}{1.00} \right)$$
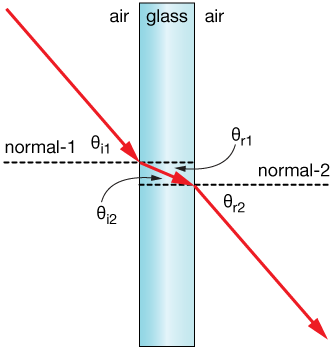
The exit angle turns out to be the same as the entrance angle,
$$\theta_{r2} = 50˚$$
That's the way it is for beams entering flat panes of glass. The image is shifted a bit, but the entrance and exit angles will be the same. Whenever you look at an image not at 90˚ to a window, you're actually seeing it shifted slightly to the left or right. You might get some roundoff error in calculations like this using the sine function, but if you keep enough digits in your intermediate calculations, the outgoing angle should match the incoming angle.
Example 2
A beam of light passes into a prism, a piece of glass with the cross-section of an equilateral triangle, such that it enters one side parallel to the base. Calculate the total angle of bending of this beam as it passes through the prism.

With 30˚ as our first angle of incidence, we can calculate the angle of the beam from the normal inside the glass. Snell's law, rearranged to solve for the angle of refraction, is
$$\theta_r = \sin^{-1} \left( \frac{n_{air} \, \sin(\theta_i)}{n_{glass}} \right)$$
Plugging in the the angle and the indices of refraction gives us
$$\theta_r = \sin^{-1} \left( \frac{1.00 \, \sin(30˚)}{1.52} \right)$$
So the first refraction angle, with respect to the surface normal on the left side of the prism, is
$$\theta_r = 19.205˚$$
Now the two surface normals in the diagram above must meet at a 120˚ angle, and if the angle of refraction of the incoming beam is 19.205˚, then 180˚ - 19.205˚ gives us the angle of incidence with the right-side surface normal, $\theta_i = 40.795^{\circ}$.
In the same way as we did for the first angle, we can now solve for the second angle of refraction, as the beam emerges from glass into air:
$$\theta_r = \sin{-1} \left( \frac{n_{glass} \, \sin(\theta_i)}{n_{air}} \right)$$
Plugging in the angle and the indices of refraction gives
$$\theta_r = \sin{-1} \left( \frac{1.53 \, \sin(40.795˚)}{1.00} \right)$$
which gives us the final angle of refraction.
$$\theta_r = 89˚$$
Here's the diagram with all of the angles:
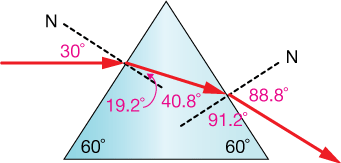
The supplementary angle to 88.8˚ is 91.2˚, and if we subtract 30˚ from that we get an overall downward angle from the initial beam striking the prism of 61.2˚.
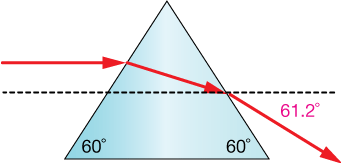
The geometry of the prism leads to large overall bending of the beam. Because the colors of white light bend differently (see below), the prism shape is ideal for separating those colors by refraction.
Wavelength dependence of refraction
A prism is not only a terrific refractor of visible light, but it is also capable of separating that light into individual color "bands." You have probably seen the familiar rainbow of colors dispersed when white light (such as sunlight) passes through a prism.
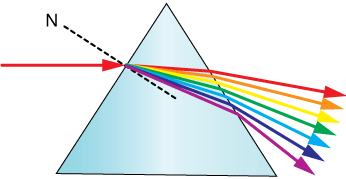
Apparently, there is some dependence the amount of refraction on the wavelength of the light. It's really on the refractive index of the material. Here's how that works: First, we know that the index of refraction of a transparent material is the ratio of the speed of light in vacuum to the speed of light in the material:
$$n = \frac{c}{v}$$
Now $c$ is the speed of light in vacuum, and we'll set it equal to $\lambda_o \, \nu_o$, the product of the wavelength and frequency of the light in vacuum. Likewise, the speed of light in the material is $v=\lambda \, \nu_o$, Here I've put the frequencies (Greek letter nu) in red to distinguish them from the velocity v.
$$c = \lambda_o \, \color{#E90F89}{\nu_o} \phantom{00000} v = \lambda \, \color{#E90F89}{\nu_o}$$
The key is that as light passes through a medium other than vacuum, its frequency doesn't change, only its wavelength. The spacing in time between peaks of an EM wave entering and passing through a medium is constant, but because of the change in speed, the spacing between those peaks is different. Here's a little animation that might help to illustrate the phenomenon. A wavefront with a certain wavelength passes through a medium (blue box) in which the speed is about 65% of the speed outside it.
You can see that the waves "stack up" a little tighter as they pass through the box, then expand again on the other side. Play the animation a few times until you see it clearly.
You might have noticed this same kind of thing if you're a skier. Detachable chair lifts do the same sort of thing at the top and bottom of the lift, where the chairs detach from the rope, slow and decrease spacing. The are spaced back out again when they reattach for the second part of the ride, but the number of chairs that pass any point in a given time (frequency) is always the same.
Constant frequencies means that we can cancel the frequencies in this new expression for the index of refraction:
$$ \require{cancel} n = \frac{\lambda_o \cancel{\nu_o}}{\lambda \cancel{\nu_o}}$$
So we have a formula for the index of refraction as a function of the wavelength of light, or the ratio of the wavelength in vacuum to the wavelength in the medium:
$$n = \frac{\lambda_o}{\lambda}$$
When the speed of light in a substance is lower than vacuum or air (very close to vacuum), then the wavelength must be reduced to produce that lower speed $(c = \lambda \, \nu).$
This means that the index of refraction for long wavelengths is smaller than for shorter wavelengths. That matches our dispersed rainbow of colors from the prism: Red is the least-bent of the colors and violet the most.
Why the sky is blue
Daytime
The sky is not blue because it reflects the oceans. Sorry, not true.
The daytime sky is blue because air has an index of refraction greater than 1 (though not much greater), and partially because that index changes with the temperature of the atmosphere.
As the diagram shows, at normal angles to the sun in daytime, colors in the blue end of the spectrum are refracted most by the atmosphere, and tend to strike the surface where we live.
It's also true that at very high altitudes the sky gets much darker, more toward the red end of the spectrum.
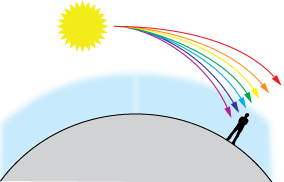
That makes sense if we're climbing into the zone where red light, which normally passes high overhead, now is more visible.
Morning and night
At sunrise and sunset we tend to see red-orange skies. That's because Earth and the sun are in a position that places the sun at or below the real horizon, the highest ground that can be seen by an observer looking toward the sun.

As the diagram shows, the atmosphere is behaving in the same way as daytime, except that now, because of the distance the rays travel through the atmosphere on their way to the observer, the rays on the violet/blue end of the spectrum bend down and strike the planet well before hitting the observer.
The rays on the red end of the spectrum, which are deflected less by the atmosphere, "survive" the trip to the observer, who sees mostly red and orange.
Mirages – seeing what's not there
You've probably been in a car on a hot day and noticed that at the end of a stretch of hot road, the roadway seems to be wet, like there's a lake ahead. That's a mirage, and it's caused by the change in refractive index between cool and warm air. Roll over or tap the desert image below to see the mirage lake at the end of this hot desert floor.

What's happening is that there is a difference between the index of refraction of the cold air above the desert and the air just above the hot sand, which radiates sunlight back into the atmosphere. This hot air layer has a relatively large index of refraction and bends light from the mountains and sky directly to the eyes of an observer on the ground.
What the observer is seeing isn't a lake at all, it's just a patch of light from the sky, the rays of which have been bent by refraction.

Lenses: convex
We can see how lenses work just using the basic rules of refraction. We'll do it qualitatively here (without numbers) just to get the general features.
![]()
First consider the beam of light moving from the left side into the lens. An interface normal is drawn there. To draw a normal to a surface, we first draw a tangent line ($T$) to the entrance point on the curve.
Then the normal ($N$) can be drawn perpendicular to that. In reality, of course, that tangent line is a plane that is tangent to a 3-dimensional lens, but this 2D representation will serve our purpose just fine.
Now Snell's law says that the angle made to the surface normal should decease in glass, which has a larger index of refraction (slower speed of light) than air. That smaller angle is drawn as the upper light beam angles down through the lens.
Now as that same beam exits the lens, the interface normal is tilted in the opposite direction. At this interface the index of refraction decreases, so the angle between the beam and the interface normal increases, further bending the light in the same direction. This biconvex lens (convex on both sides) is really a lot like the prism above, it just doesn't bend the light so dramatically.
The direction of this bending is opposite on the lower part of the lens, and beams passing through the center of the lens aren't bent at all.
A biconvex lens, or even a convex lens with one flat side (you can do the geometry on that one) serves to focus incoming light. That light can be focused to a point or any other shape if the lens is designed carefully enough.
Lenses: concave
A concave lens forms a pocket or cave on at least one side. shown here is the cross section of a biconcave lens, with concave faces on both sides.
Concave lenses are used to spread out the beams of incoming light. Start with the upper incoming beam on the left side. The angle it makes with the interface normal (which is perpendicular to the tangent line, $T$, at that point) is smaller inside the glass, where the index of refraction is smaller (speed of light is slower).
Then as the beam strikes the second interface, the normal has a nearly opposite angle (sloped down instead of up in this figure) and as the light bends away from the normal, it is further defocused.
A planar-concave lens does the same thing, only to a lesser degree. The geometry of that kind of lens is left for you to sketch out (try it!).
A combination of convex and concave lenses is used in devices like microscopes and telescopes to provide strong magnification and still make an image that the human eye can focus.
![]()
Pro tip
To remember which lens is concave and which is convex, remember that a con-cave lens makes a cave shape.
Fermat's principle of least time
Pierre de Fermat (1601-1665), who contributed richly to physics and mathematics, proposed that the path of a beam of light through any medium of combination of media was the one that took the least possible time. This is known as the principle of least time (also known as Fermat's principle).
Succintly, Fermat said that out of all possible paths between one point and another, light takes the one that takes the least time.
While Fermat's principle doesn't really tell us why light behaves in that way in matter, it does give us some foundation for rules like Snell's law.
Fermat's principle is well suited for using techniques of differential calculus, particularly optimization using the derivative. That is illustrated in the derivation of Snell's law at the bottom of this page.
One example of such a problem is this:
Imagine that you are on the beach and you spot someone offshore who looks to be drowning (figure below). You need to run and swim to reach that person, and it's important that you do it in the least time. You could jump in the water where you are and swim the long diagonal path, but you swim more slowly than you run. You could run until the victim is perpendicular to the beach and you have to swim through the least-possible water, but that's probably not the optimal (least time) path either. The optimal path is somewhere in between.

It's the same for light. Take a look at the diagram below. It shows light passing from air through two different transparent media (green and blue) with different indices of refraction, and then back into air. It's a sketch of light traveling from point $A$ to point $B$ through zones in which the speed is different (like your speed on sand and in water).
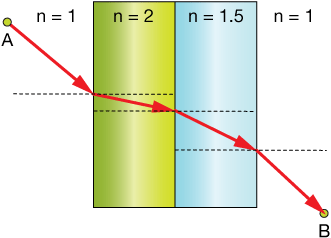
In the green medium, the speed is slower (larger n), so the beam takes a more direct path through it (closer to perpendicular) to minimize the time. Relative to the green zone, light travels faster through the blue medium, so it can bend and spend a little more time there before emerging and proceeding through $B$. That's the fastest path, and it's faster than if we just drew a straight beam from $A$ to $B$.
Now if our beam had entered at a right angle to those to slabs of material, the fastest path through would have been a straight line. It changes when that first angle of incidence changes.
Derivation of Snell's law (calculus )
In this section we show how to derive Snell's law of refraction using the principle of least time. It involves differential calculus, so if you aren't comfortable with that yet, don't fear. Just use the law and come back to it when you can.
Here's the setup. A beam of light of length d1 propagating through a medium with speed of light s1 strikes a material (blue) with a speed of light s2. Other dimensions necessary for the derivation are shown.

Our strategy will be to find the total time it will take to travel from a point in the first medium to a known point in the second. The principle of least time always applies to optics, and it says that light will always take a path that ensures that it travels from place to place in the shortest-possible time. We begin by rearranging the definition of speed:
$$s = \frac{d}{t} \; \longrightarrow \; t = \frac{d}{s}$$
The two distances, $d_1$ and $d_2$, can be rewritten using the Pythagorean theorem:
$$t = \frac{\sqrt{x^2 + h^2}}{s_1} + \frac{\sqrt{(a - x)^2 + y^2}}{s_2}$$
Now we take the derivative of that expression with respect to the variable $x$, which we'll relate to our angles later, setting the derivative to zero to find the minimum in the time:
$$ \begin{align} \frac{dt}{dx} &= \frac{\frac{1}{2}(x^2 + h^2)^{-1/2} \cdot 2x}{s_1} \\[5pt] &+ \frac{\frac{1}{2}((a - x)2 + y^2)^{-1/2} \cdot 2(a - x)(-1)}{s_2} = 0 \end{align}$$
Some cancellation and rearranging gives:
$$\frac{x}{s_1\sqrt{x^2 + h^2}} + \frac{-(a - x)}{s_2\sqrt{(a - x)^2 - y^2}} = 0$$
We can add the second term to both sides to get an equality:
$$\frac{x}{s_1 \sqrt{x^2 + h^2}} = \frac{a - x}{s_2\sqrt{(a - x)^2 + y^2}}$$
Now recall that
$$ \begin{align} d_1 &= \sqrt{x^2 + h^2} \text{ and} \\[5pt] d_2 &= \sqrt{(a - x)^2 + y^2} \end{align}$$
Hold on to that for a minute and consider the sines of the angles of incidence and refraction:
$$ \begin{align} \sin(\theta_i) &= \frac{x}{\sqrt{x^2 + h^2}} \text{ and} \\[5pt] \sin(\theta_r) &= \frac{a - x}{\sqrt{(a - x)^2 + y^2}} \end{align}$$
Substituting those into our equality gives
$$\frac{\sin(\theta_i)}{s_1} = \frac{\sin(\theta_r)}{s_2}$$
Now if we note that the index of refraction, $n = c/s$ ($c =$ speed of light in vacuum) can be rewritten to substitute for $1/s_1$ and $1/s_2$ in the last expression,
$$n = \frac{c}{s} \; \longrightarrow \; \frac{1}{s} = \frac{n}{c}$$
we get
$$\frac{n_1}{c} \sin(\theta_i) = \frac{n_2}{c} \sin(\theta_r)$$
The $c$'s are redundant and can be cancelled, giving Snell's law.
$$n_1 \, \sin(\theta_1) = n_2 \, \sin(\theta_2)$$
Easy peasy, lemon squeezy.
Practice problems
-
A laser beam enters the end of an optical fiber (glass fiber) at an angle of 23˚ from the normal to the end of the fiber, as shown. Calculate the angle of refraction of the beam inside the fiber if the index of refraction of the fiber is $n=1.45$.
Solution
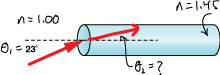
$$ \begin{align} n_1 \, \sin(\theta_1) &= n_1 \, \sin(\theta_2) \\[5pt] \frac{n_1}{n_2} \sin(\theta_1) &= \sin(\theta_2) \\[5pt] \theta_2 &= \sin^{-1} \left( \frac{n_1}{n_2} \sin(\theta_1) \right) \\[5pt] \theta_2 &= \sin^{-1} \left( \frac{1.00}{1.45} \sin(23^{\circ}) \right) = 15.6^{\circ} \\[5pt] \theta_2 &= 15.6^{\circ} \end{align}$$
-
A beam of light propagating through air ($n=1.00$) strikes a stack of transparent materials with indices of refraction as shown in the figure at an angle of 32˚. Calculate the angles of incidence and refraction all the way through the stack and calculate the overall angle of refraction of the stack with respect to the first incoming beam.
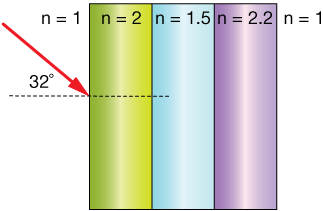
Solution
$$ \begin{align} 1-2: \; \theta &= \sin^{-1} \left( \frac{1.0}{2.0} \sin(32^{\circ}) \right) = 15.36^{\circ} \\[5pt] 2-3: \; \theta &= \sin^{-1} \left( \frac{2.0}{1.5} \sin(15.36^{\circ}) \right) = 20.69^{\circ} \\[5pt] 3-4: \; \theta &= \sin^{-1} \left( \frac{1.5}{2.2} \sin(20.69^{\circ}) \right) = 13.94^{\circ} \\[5pt] 4-5: \; \theta &= \sin^{-1} \left( \frac{2.2}{1.0} \sin(13.94^{\circ}) \right) = 32.0^{\circ} \\[5pt] \end{align}$$
-
A beam of light propagating through air ($n=1.0$) strikes the surface of a liquid at a 15˚ angle. If the refracted beam makes an 11˚ angle with the surface of the liquid, calculate the index of refraction of the liquid.
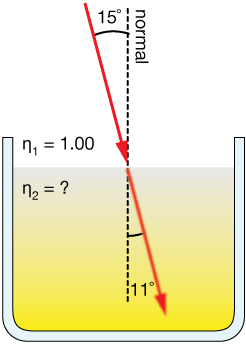
Solution
$$ \begin{align} n_1 \, \sin(\theta_1) &= n_1 \, \sin(\theta_2) \\[5pt] n_2 &= n_1 \frac{\sin(\theta_1)}{\sin(\theta_)} \\[5pt] n_2 &= 1.00 \frac{\sin(15^{\circ})}{\sin(10^{\circ}} \\[5pt] n_2 &= 1.49 \end{align}$$
-
A light ray moving through a rectangular slab of material called CR39 (n = 1.498) at an angle of 49˚ enters another medium at an angle of 41˚. Calculate the index of refraction of the second medium. CR39 is a plastic commonly used for eyeglasses.
Solution
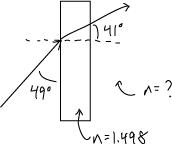
$$ \begin{align} n_1 \, \sin(\theta_1) &= n_1 \, \sin(\theta_2) \\[5pt] n_2 &= n_1 \frac{\sin(\theta_1)}{\sin(\theta_)} \\[5pt] n_2 &= 1.498 \frac{\sin(49^{\circ})}{\sin(41^{\circ}} \\[5pt] n_2 &= 1.72 \end{align}$$

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.