In order to really understand and be able to work problems in advanced algebra, calculus, probability and statistics, you really need to get good at manipulating variables and numbers with exponents. It's one of those things you just can't skip. You can learn more in these sections,
... but make sure to learn this section very well first.
Exponents are explicit instructions
In this section we'll explore numbers (or variables) with rational and/or negative exponents (they can be combined). Each type of exponent has a specific meaning. Rational exponents combine powers and roots of the base, and negative exponents indicate that the reciprocal of the base is to be used.
Recall that a rational number is one that can be expressed as a ratio of integers, like 21/4 or 2/5. Irrational numbers like $\pi$ or $e$ cannot be so represented.
Here are some examples of the kinds of numbers or expressions* we'll be working with:
$$3^{\frac{2}{3}} \phantom{0000} x^{-2} \phantom{0000} 4^{\frac{a}{b}} \phantom{0000} 27^{-5/2} \phantom{0000} \left( \frac{2}{7} \right)^{-3}$$
*Pro tip
An equation has an equal sign. An expression is some snippet like a number or numbers and variables with or without operations ( $+ \; - \; \times \; \div$ ) without an equal sign.
$$\bf \text{Equations}$$
$$y = mx + b$$
$$2x^2 + 3 = 4x$$
$$\frac{2x - 1}{x^2} = \frac{1}{3}$$
$$\bf \text{Expressions}$$
$$27x^3$$
$$-9a^2 + 14b - c$$
$$\frac{4}{3} x^7$$
Refresher: The laws of exponents
Let's use some numerical examples, all powers of two because they're convenient, to derive the most important laws of exponents. First, some quick definitions

We understand that $x^n$ means to multiply $x$ by itself $n$ times, so that $2^3 = 2 \cdot 2 \cdot 2$, and so on.
Now let's multiply numbers with the same base:
$$ \begin{align} 2^2 \cdot 2^3 &= (2 \cdot 2)(2 \cdot 2 \cdot 2) \\[5pt] &= 2^5 = 2^{2 + 3} \end{align}$$
The rule for multiplying powers of a common base is
$$x^a \cdot x^b = x^{a + b}$$
We just add exponents. Look back at the example and make sure you understand why.
Now division, again with powers of two:
$$\frac{2^3}{2^2} = \frac{2\cdot 2\cdot 2}{2\cdot 2} = 2^1 = 2^{3 - 2}$$
So to divide powers of the same base, we just subtract exponents.
$$\frac{x^a}{x^b} = x^{a - b}$$
And finally, let's raise a power to a power:
$$ \begin{align} (2^3)^2 &= (2 \cdot 2 \cdot 2)^2 \\[5pt] &= (2 \cdot 2 \cdot 2)(2 \cdot 2 \cdot 2) \\[5pt] &= 2^3 \cdot 2^3 = 2^{3 \cdot 2} \end{align}$$
To raise a power to a power, simply multiply exponents:
$$(x^a)^b = x^{a \cdot b}$$
Here is a table of the laws of exponents. Tap/click here to download a copy for your notes.
Laws of Exponents
| product | $a^m \cdot a^n = a^{m+n}$ |
$2^2 \cdot 2^2 = (2 \cdot 2)(2 \cdot 2 \cdot 2) = 2^5$ |
| Quotient | $\frac{a^m}{a^n} = a^{m-n}$ |
$\frac{2^3}{2^2} = \frac{2 \cdot 2 \cdot 2}{2 \cdot 2} = 2^{3-1} = 2$ |
| Power | $(a^m)^n = a^{m \cdot n}$ |
$2^2)^3 = (2\cdot 2\cdot 2)(2\cdot 2\cdot 2)(2\cdot 2\cdot 2)=2^9$ |
| Inverse | $a^{-1}=\frac{1}{a}$ |
$2^{-1}=\frac{1}{2}\phantom{000}$ |
| Zero Exponent |
$a^0=1$ | $2^0=1\phantom{000}$ |
Why does $x^0=1$ ?
This isn't really a proof, but think about it like this (using the laws of exponents). Notice that
$$x^0 = x^{1-1}$$
Now according to the product property of exponents,
$$x^{1-1} = x^1 \, \cdot \, x^{-1}$$
Using the reciprocal proerty gives
$$x^1 \cdot x^{-1} = x \cdot \frac{1}{x} = 1.$$
Now x is a variable, so anything raised to the zero power is one.
Why does $x^{-1}$ mean $\frac{1}{x}$ ?
We know that $x^n$ means $x$ multiplied by itself $n$ times. For example,
$$ \begin{align} x^2 &= x \cdot x \\[5pt] x^3 &= x \cdot x \cdot x \\[5pt] x^4 &= x \cdot x \cdot x \cdot x \; \dots \end{align}$$
We can interpret $x^2$ as $1 \cdot x \cdot x,$ and so on.
So we can interpret negative exponents as repeated divisions:
$$ \begin{align} x^{-1} &= \frac{1}{x} \\[5pt] x^{-2} &= \frac{1}{x} \cdot \frac{1}{x} \\[5pt] x^{-3} &= \frac{1}{x} \cdot \frac{1}{x} \cdot \frac{1}{x}, \end{align}$$
where we recall that dividing by $x$ is the same as dividing by $\frac{1}{x}.$
Negative exponents
Let's begin with the exponent -1. It means "take the reciprocal." So

It's just that simple. We define $x^{-1}$ to mean $1/x$. Now we can use the power law of exponents to extend that property to any negative exponent. For example, here are two ways of looking at $x^{-2}$:
$$ \begin{align} x^{-2} &= (x^{-1})^2 = \left( \frac{1}{x} \right)^2 = \frac{1}{x^2} \\[5pt] &= (x^2)^{-1} = \frac{1}{x^2} \end{align}$$
In the first way we take the square of $1/x$, and in the second we take the inverse of $x^2$. Both lead to the same result. You will find that you have a lot of freedom about how to use negative exponents when you work problems. There will usually be a couple of ways to get a solution.
The general formula for a negative exponent is thus

In the examples that follow, the idea will be to rewrite each expression so that it has no negative exponents. In these examples I'll take meticulous steps. I hope you'll eventually learn how to cut some corners, but for now, seeing these problems done in great detail might be helpful. Try to follow and understand the logic behind each step.
The exponent -1 means "take the reciprocal."
Example 1
$$2^{-1} = \frac{1}{2}$$
This one is pretty simple. The exponent -1 means "take the reciprocal, and the reciprocal of 2 is $\frac{1}{2}$.
Example 2
$$\frac{1}{x^{-1}} = \frac{1}{\frac{1}{x}} = 1 \cdot \frac{x}{1} = x$$
We'll take this one step-by-step. (1) Take the reciprocal of the denominator; now you have a fraction in the denominator. (2) Dividing by a fraction is the same as multiplying by the reciprocal. (3) 1 divides into 1 to give $1\cdot x = x$. That's it.
Example 3
Work your way through the steps of this conversion:
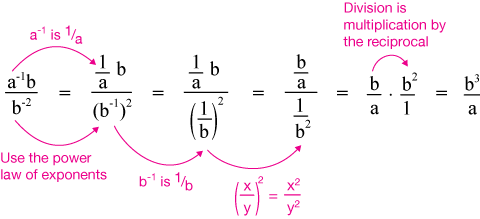
Example 4
Work your way through the steps of this conversion. As is so often true of these expressions when they get complicated, there is more than one way to simplify this one. Two are shown:

Practice problems
Simplify each expression as much as possible, and so that it contains no negative exponents.
-
$$5^{-2}$$
Solution
$$5^{-2} = \frac{1}{5^2} = \frac{1}{25}$$
-
$$\frac{5}{5^{-1}}$$
Solution
$$\frac{5}{5^{-1}} = \frac{5}{\frac{1}{5}} = 5 \cdot \frac{5}{1} = 25$$
-
$$25 \cdot 5^{-1}$$
Solution
$$25 \cdot 5^{-1} = 25 \cdot \frac{1}{5} = \frac{25}{5} = 5$$
-
$$\frac{a^{-2}}{a}$$
Solution
$$= a^{-2} \cdot \frac{1}{a} = \frac{1}{a^2} \cdot \frac{1}{a} = \frac{1}{a^3}$$
-
$$\frac{a b^{-2}}{b^{-3}}$$
Solution
$$= a \cdot \frac{b^3}{b^2} = a b^{3 \cdot 2} = ab$$
-
$$\frac{11 a c^{-2}}{(abc)^{-1}}$$
Solution
$$= \frac{11 a \frac{1}{c^2}}{\frac{1}{abc}} = \frac{11 a}{c^2} \cdot abc = \frac{11 a^2 b}{c}$$
-
$$\frac{1}{6a} \cdot a^{-3}$$
Solution
$$= \frac{1}{6a} \cdot \frac{1}{a^3} = \frac{1}{6 a^4}$$
-
$$\frac{2 x y^{-3}}{x^4 y z^{-2}}$$
Solution
$$= \frac{2}{1} \cdot \frac{x}{x^4} \cdot \frac{1}{y^3 y} \cdot \frac{z^2}{1} = \frac{2 z^2}{x^3 y^4}$$
-
$$4 c^2 \cdot \frac{b^2 c^{-2}}{b^{-2} c^2}$$
Solution
$$= \frac{4 b^2 c^{-2}}{b^{-2}} = \frac{4 b^2 b^2}{c^2} = \frac{4 b^4}{c^2}$$
-
$$\frac{\frac{1}{6} \cdot \frac{2}{x^{-2}}}{3}$$
Solution
$$= \frac{\frac{1}{3 x^{-2}}}{3} = \frac{x^2}{3} \cdot \frac{1}{3} = \frac{x^2}{9}$$
-
$$\left( \frac{1}{x^{-2}} \right)^{-3}$$
Solution
$$= \left( \frac{x^{-2}}{1} \right)^3 = \left( \frac{1}{x^2} \right)^3 = \frac{1^3}{(x^2)^3} = \frac{1}{x^6}$$
-
$$\left( \frac{x^2}{y^{-2}}\right) xy^{-1}$$
Solution
$$= \frac{x^2 x y^2}{y} = x^3 y$$
Rational exponents
Rational exponents are fractional exponents (rational → "ratio"), where both the numerator and denominator of the fraction are non-zero integers.
The numerator of a rational exponent is the power to which the base is to be raised, and the denominator is the root of the base to be taken.
Rational exponents may be positive or negative with the same meaning for negative roots as above. It looks like this:

Here are four examples of rational exponents and their meanings:


The numerator of a rational exponent is the power to which the base is raised, and the denominator is the root. The order in which these are evaluated doesn't matter, though one way may sometimes be easier than the other.
Example 5: Evaluate 84/3
$$ \begin{align} 8^{\frac{4}{3}} &= \sqrt[3]{8^4} \\[5pt] &= \sqrt[3]{4096} = 16 \end{align}$$
OR
$$ \begin{align} 8^{\frac{4}{3}} &= (\sqrt[3]{8})^4 \\[5pt] &= 2^4 = 16 \end{align}$$
Notice that 84/3 can be interpreted as (1) The cube root of 8 to the 4th power, or (2) The 4th power of the cube-root of 8. Either is valid and each leads to the same result.
Example 6: Evaluate 9-3/2
$$ \begin{align} 9^{-\frac{3}{2}} &= \sqrt{9^{-3}} \\[5pt] &= \sqrt{\frac{1}{9^3}} \\[5pt] &= \sqrt{\frac{1}{729}} = \frac{1}{27} \end{align}$$
OR
$$ \begin{align} 9^{-\frac{3}{2}} &= (\sqrt{9})^{-3} \\[5pt] &= 3^{-3} \\[5pt] &= 27^{-1} = \frac{1}{27} \end{align}$$
Notice that 9-3/2 can be interpreted as (1) The square root of the inverse of 9 cubed, or (2) the inverse of the cube of the square root of 9. Which you decide to use is up to you.
Video examples
Solving problems involving rational and/or negative exponents
These videos will take you through the solutions of several kinds of problems you might encounter using rational and negative exponents, alone or in combinations.
Examples — 1
Here are three whole numbers raised to rational powers to give you an idea of how these can be simplified exactly and pretty quickly without a calculator. You just need to know the laws of exponents (and remember the multiplication table). The last example shows you how to solve a problem like $x^{a/b} = 25$, by raising both sides to the $b/a$ power.
Examples — 2
Here are two more examples, the first like the last on the previous video, only with a negative rational exponent on $x$. The second example is of the kind you'll encounter often: a ratio of several variables raised to various rational and negative powers. One strategy (used here) is to deal with the negative exponents first, by moving them across the division line and dropping the negative sign.
Examples — 3
Here are two more examples of simplifying ratios of variables raised to rational and negative powers.
Practice problems
Simplify the following as far as you can:
-
$$49^{\frac{3}{2}}$$
Solution
$$= (\sqrt{49})^3 = 7^3 = 49 \cdot 7 = 343$$
OR
$$= \sqrt{49^3} = \sqrt{117649} = 343$$
-
$$64^{\frac{5}{6}}$$
Solution
$$= \left( \sqrt[6]{64} \right)^5 = 2^5 = 32$$
-
$$32^{-\frac{3}{5}}$$
Solution
$$ \begin{align} &= \left( \frac{1}{32} \right)^{\frac{3}{5}} = \left( \sqrt[5]{\frac{1}{32}} \right)^3 \\[5pt] &= \left( \frac{1}{2} \right)^3 = \frac{1}{8} \end{align}$$
-
$$4096^{\frac{3}{4}}$$
Solution
$$= \left( 4096^{\frac{1}{4}} \right)^3 = 8^3 = 512$$
-
$$\left( \frac{1}{36} \right)^{-\frac{1}{2}}$$
Solution
$$= 36^{\frac{1}{2}} = \sqrt{36} = 6$$
-
$$343^{-\frac{2}{3}}$$
Solution
$$= \left( \frac{1}{343} \right)^{\frac{2}{3}} = \frac{1}{7^2} = \frac{1}{49}$$
Problems (7-9) Solve for $x$ by applying the reciprocal exponent to each side of the equation.
-
$$x^{\frac{2}{3}} = 16$$
Solution
$$ \begin{align} \left( x^{\frac{2}{3}} \right)^{\frac{3}{2}} &= 16^{\frac{3}{2}} \\[5pt] x &= 4^3 = 64 \end{align}$$
-
$$x^{\frac{1}{5}} = 2$$
Solution
$$ \begin{align} \left( x^{\frac{1}{5}} \right)^{\frac{5}{1}} &= 2^5 \\[5pt] x &= 32 \end{align}$$
-
$$x^{-\frac{2}{3}} = \frac{1}{9}$$
Solution
$$ \begin{align} \left( x^{-\frac{2}{3}} \right)^{-\frac{3}{2}} &= \left( \frac{1}{9} \right)^{-\frac{3}{2}} \\[5pt] x &= 9^{\frac{3}{2}} = 3^3 = 27 \end{align}$$
Problems (10-12) Reduce these expressions as far as possible, so that your result contains only one instance of each variable and no negative exponents.
-
$$\frac{x^{\frac{3}{4}} y^{\frac{1}{2}} z}{x^{-\frac{1}{2}} y z^{\frac{3}{2}}}$$
Solution
$$= \frac{x^{\frac{3}{4} + \frac{1}{2}}}{y^{1 - \frac{1}{2}} z^{\frac{3}{2} - 1}} = \frac{x^{\frac{5}{4}}}{y^{\frac{1}{2}} z^{\frac{1}{2}}}$$
When the degree of the variable in the denominator is greater than its corresponding variable in the numerator, I'm subtracting toward (num. - denom.) the denominator, as a shortcut.
-
$$\frac{a^{-\frac{3}{4}} b^{\frac{4}{3}}}{27^{\frac{1}{3}} a^2}$$
Solution
$$\frac{b^{\frac{4}{3}}}{\frac{1}{3} a^{\frac{3}{4} + 2}} = \frac{3 b^{\frac{4}{3}}}{a^{\frac{11}{4}}}$$
-
$$\frac{3 x^{\frac{1}{3}} z^{-2}}{x^2 y^2 z^{\frac{1}{2}}}$$
Solution
$$= \frac{3}{x^{2 - \frac{2}{3}} y^2 z^{\frac{1}{2} + 2}} = \frac{3}{x^{\frac{4}{3}} y^2 z^{\frac{5}{2}}}$$

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.
