Derivatives of quotients of functions: $f(x)/g(x)$
In this section we'll develop the quotient rule of derivatives then apply it in order to extend the power rule to negative-integer exponents.
The quotient rule is a prescription for finding the derivative of a quotient of functions. Here is the formula first, then we'll derive it below.
The quotient rule
The derivative of a quotient of functions is the denominator function multiplied by the derivative of the numerator function, minus the numerator function multiplied by the denominator, and all divided by the square of the denominator function.
$$\frac{d}{dx} \left[ \frac{f(x)}{g(x)} \right] = \frac{g(x) \cdot \frac{d}{dx} f(x) - f(x) \cdot \frac{d}{dx} g(x)}{[g(x)]^2}$$
If f(x) is the numerator and g(x) is the denominator, then we can abbreviate that definition like this:
$$\left( \frac{f}{g} \right)' = \frac{gf' - fg'}{g^2}$$
Derivation of the quotient rule
The quotient rule can easily be derived using the difference quotient and a simple trick. Start by writing out the difference quotient for, $f(x)/g(x)$. This derivation is really just like that of the product rule in another section.
$$\frac{d}{dx} \frac{f(x)}{g(x)} = \lim_{h\to 0} \frac{1}{h} \left[ \frac{f(x + h)}{g(x + h)} - \frac{f(x)}{g(x)} \right]$$
As usual, give these fractions a common denominator:
$$= \lim_{h\to 0} \frac{1}{h} \left[ \frac{f(x + h) g(x) - g(x + h) f(x)}{g(x) g(x + h)} \right]$$
Now the that will help us pull out some recognizable derivatives: add and subtract $f(x)\cdot g(x)$ to the numerator. The net result, of course, is doing nothing at all, but you'll see how it will help:
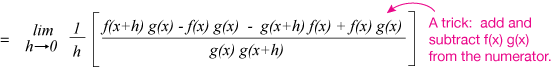
Now rearrange, factoring $g(x)$ out of the first term of the numerator and $f(x)$ out of the second:
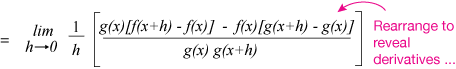
... separate the terms and switch around the denominator to get closer to derivatives:
$$= \lim_{h\to 0} \frac{1}{g(x) g(x + h)} \left[ \frac{g(x)[f(x + h) - f(x)]}{h} - \frac{f(x) [g(x + h) - g(x)]}{h} \right]$$
Use the properties of limits to isolate terms and identify the derivatives, $f'(x)$ and $g'(x)$:
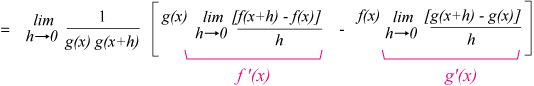
Finally, in the limit as $h$ approaches zero, $g(x+h)$ is $g(x)$, so long as $g(x)$ is a continuous function. In other words, $g(x)$ must have a value at $x$.
$$\lim_{h\to 0} \frac{g(x) f'(x) - f(x)g'(x)}{g(x) g(x + h)} = \frac{g(x) f'(x) - f(x)g'(x)}{[g(x)]^2}$$
A mnemonic
The quotient rule can be remembered using this mnemonic phrase:
the square of what's below.
It means take what's in the denominator (low), multiply it by the derivative (d) of the numerator (high), subtract the opposite pairing, then divide the whole thing by the square of the denominator.
Example 1
Our function is
$$f(x) = \frac{x^4}{\sin(x)}$$
$$f'(x) = \frac{\sin(x) \frac{d}{dx} x^4 - x^4 \frac{d}{dx} \sin(x)}{\sin^2(x)}$$
The result is
$$ = \frac{3x^2 \sin(x) - x^4 \cos(x)}{\sin^2(x)}$$
Example 2
Our function is
$$f(x) = \frac{x(x - 3)}{x^3 - 2}$$
$$f'(x) = \frac{(x^3 - 2) \frac{d}{dx} (x^2 - 3x) - (x^2 - 3x) \frac{d}{dx} (x^3 - 2)}{(x^3 - 2)^2}$$
After taking the simple derivatives, we get this function. Remember to keep expressions in parenthesis:
$$= \frac{(x^3 - 2)(2x - 3) + (x^2 - 3x)(3x^2)}{(x^3 - 3)^2}$$
Now we can take a couple of algebra steps to simplify this one. First multiply the binomials of the numerator:
$$= \frac{2x^4 - 3x^3 - 4x + 6 + 3x^4 - 9x^3}{(x^3 - 2)^2}$$
Gather terms. I've left the denominator alone here. It's about as simple as it will get.
$$= \frac{5x^4 - 12x^3 - 4x + 6}{(x^3 - 2)^2}$$
AP Calculus Pro tip:
If you intend to take the AP calculus exam (AB or BC), it's not necessary to simplify most of your answers to open-response questions. The AP exam is designed to be a test of calculus and not just algebra. If you find a perfectly fine derivative on the AP test, but you make an error simplifying your result, graders may have no choice but to subtract a point or two. So don't simplify on the AP exam. In real life, we generally simplify when we can, however.
Practice problems
Find the derivative of each function using the quotient rule.
To view wide solutions on a narrow screen, scroll left ↔ right
-
$$f(x) = \frac{x^2 - 4x - 3}{x + 3}$$
Solution
$$ \begin{align} f'(x) &= \frac{(2x - 3)(1) - (x - 2)(2)}{(2x - 3)^2} \\[5pt] &= \frac{2x - 3 - 2x + 4}{(2x - 3)^2} \\[5pt] &= \frac{1}{(2x - 3)^2} \end{align}$$
-
$$f(x) = \frac{x - 2}{2x - 3}$$
Solution
$$ \begin{align} f'(x) &= \frac{(2x - 3)(1) - (x - 2)(2)}{(2x - 3)^2} \\[5pt] &= \frac{2x - 3 - 2x + 4}{(2x - 3)^2} \\[5pt] &= \frac{1}{(2x - 3)^2} \end{align}$$
-
$$f(x) = \frac{12}{x^2}$$
Solution
$$ \begin{align} f'(x) &= \frac{x^2(0) - 12(2x)}{x^4} \\[5pt] &= \frac{24x}{x^4} \\[5pt] &= \frac{24}{x^3} \end{align}$$
-
$$f(x) = \frac{x^4 + 5x^3 - \sqrt{x}}{x^2}$$
Solution
$$ \begin{align} f'(x) &= \frac{x^2(4x^3 + 15x^2 -\frac{1}{2}x^{-1/2}) - (x^4 + 5x^3 - x^{1/2})(2x)}{x^4} \\[5pt] &= \frac{4x^5 + 15x^4 - \frac{1}{2} x^{3/2} - 2x^5 - 10x^4 + 2x^{3/2}}{x^4} \\[5pt] &= \frac{2x^5 + 5x^4 + \frac{3}{2} x^{3/2}}{x^4} \\[5pt] &= 2x + 5 + \frac{3}{2} x^{-1/2} \\[5pt] &= 2x + 5 + \frac{3}{2 \sqrt{x}} \end{align}$$
-
$$f(x) = A - \frac{B}{x} - \frac{C}{x^2}$$
Solution
$$ \begin{align} f'(x) &= 0 - \left( \frac{x(0) - B}{x^2} \right) - \left( \frac{x^2(0) - 2xC}{x^4} \right) \\[5pt] &= -\left( \frac{-B}{x^2} \right) - \left( \frac{-2xC}{x^4} \right) \\[5pt] &= \frac{B}{x^2} + \frac{2xC}{x^4} \end{align}$$
-
$$f(x) = \frac{x + \sqrt{x}}{x^{1/3}}$$
Solution
$$ \begin{align} f'(x) &= \frac{x^{1/3}(1 + \frac{1}{2} x^{-1/2}) - (x + x^{1/2})(\frac{1}{3} x^{-2/3})}{x^{2/3}} \\[5pt] &= \frac{x^{1/3} + \frac{1}{2} x^{-1/6} - \frac{1}{3} x^{1/3} - \frac{1}{3} x^{-1/6}}{x^{2/3}} \\[5pt] &= x^{-2/3}\left( \frac{2}{3} x^{1/3} + \frac{1}{6} x^{-1/6}\right) \\[5pt] &= \frac{2}{3} x^{-1/3} + \frac{1}{6} x^{-5/6} \end{align}$$
-
$$f(x) = \frac{cx}{1 + cx}$$
Solution
$$ \begin{align} f'(x) &= \frac{(1 + cx)c - cx(c)}{(1 + cx)^2} \\[5pt] &= \frac{c + cx^2 - cx^2}{(1 + cx)^2} \\[5pt] &= \frac{c}{(1 + cx)^2} \end{align}$$
-
$$f(x) = \frac{ax - b}{cx - d}$$
Solution
$$ \begin{align} f'(x) &= \frac{(cx - d)(a) - (ax - b)(c)}{(cx - d)^2} \\[5pt] &= \frac{acx - ad - acx + bc}{(1 + cx)^2} \\[5pt] &= \frac{bc - ad}{(cx - d)^2} \end{align}$$
-
$$f(x) = \frac{x^6 + 2x^3 - 5}{x^2}$$
Solution
$$ \begin{align} f'(x) &= \frac{x^2(6x^5 + 6x^2) - (x^6 + 2x^3 - 5)(2x)}{x^4} \\[5pt] &= \frac{6x^7 + 6x^4 - 2x^7 - 4x^4 + 10x}{x^4} \\[5pt] &= \frac{4x^7 + 2x^4 + 10}{x^4} \\[5pt] &= \frac{4x^6 + 2x^3 + 10}{x^3} \end{align}$$
-
$$f(x) = \frac{x^2}{1 - 2x}$$
Solution
$$ \begin{align} f'(x) &= \frac{(1 - 2x)(2x) - x^2(-2)}{(1 - 2x)^2} \\[5pt] &= \frac{2x - 4x^2 + 2x^2}{(1 - 2x)^2} \\[5pt] &= \frac{2x - 2x^2}{(1 - 2x)^2} \\[5pt] &= \frac{2x(1 - x)}{(1 - 2x)^2} \end{align}$$
Must I memorize the quotient rule?

Being a being with a small brain, I don't always use the quotient rule when I need to find the derivative of a quotient. I don't have a lot of extra space in there, so I don't like the clutter.
In fact, any function $f(x)/g(x)$ can be written as the product $f(x)[g(x)]^{-1}$. So the product rule will take you a long way in finding derivatives of quotients.
Still, the quotient rule does make a lot of derivatives much easier in the long run. So memorization is up to you, but it helps to have the memory device: low-d-hi minus hi-d-low over the square of what's below. Who could forget that?
Extension of the power rule to negative exponents
Up to this point, it's unlikely that you've developed the power rule of derivatives,
$$\frac{d}{dx} \, x^n = n \, x^{n - 1}$$
for negative exponents, such as the derivative of f(x) = x-1. We can do that now very easily with the quotient rule. Here's the derivative:
$$\frac{d}{dx} \, x^{-n} = \frac{d}{dx} \left[ \frac{1}{x^n} \right]$$
Applying the quotient rule, we get:

Now notice that the derivative of a constant is zero, and for the second derivative, we can use the power rule with a positive exponent. Condensing the result gives:
$$= \frac{-n x^{n - 1}}{x^{2n}}$$
Now we can use the laws of exponents (namely that $1/(2^n) = 2^{-n}$, and $x^a \cdot x^b = x^{a+b}$, to get our result:
$$\frac{-n \, x^{n - 1}}{x^{2n}} = -n \, x^{n - 1 - 2n} = -n \, x^{-n - 1}$$
... which is pretty much what we would have guessed, I guess.
Video examples
Here are eight examples (four videos) of quotient-rule derivatives. Enjoy! (OK, maybe that's overdoing it. I do hope they're helpful, though).
Example 1
The first of these two examples is a rational function. In the second, we find the derivative of the tangent function by finding the derivative of $\sin(x)/\cos(x)$ with the quotient rule.
Minutes of your life: 0:00
Example 2
In the first example, we find the derivative of $f(x) = 1/x$. In the second, the derivative of a quotient that includes an exponential function.
Minutes of your life: 0:00
Example 4
In these two examples we show that we can find the derivative of reciprocal trigonometric functions, like $\cot(x)$ or $\csc(x)$ using the quotient rule.
Minutes of your life: 0:00
Example 4
Here are a couple more slightly more complicaed quotient rule examples.
Minutes of your life: 0:00
mnemonic
(nee-mon-ick)
A mnemonic device, like an acronym (ROYGBIV, NASA) or a phrase (Every Good Boy Does Fine) is a device you might use to jog your memory of something more complicated.

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.