This section on pressure is related to the section on Pascal's principle, which explains how hydraulics work. You might want to check that out, too.
Pressure is force divided by area
It matters how much the force is spread out.
It actually matters very much how an applied force is spread out both in space and in time, but we'll just think about space here.
Here's a little thought experiment. You have a choice of a force of 100 N (about 22 lbs.) being applied to the back of your hand either (1) through the tip of a nail, or (2) through a hand-sized piece of flat wood placed on top of your hand.
In the first case the force is applied to a very small point, and our experience tells us that a sharp enough nail would even penetrate the skin.
In the second, although having that weight on our hands for a long time might get uncomfortable, we wouldn't worry about the board penetrating our skin. The force is more "spread out."
The difference between the two scenarios is the area over which the force is applied. In case (1) the area is very small, and in case (2), it's about as large as it can be relative to the size of a hand.
A classic case of this kind of thing is the proverbial bed of nails. Here an Indian swami lounges on a bed of nails, possible because the total force of his body on the nails is spread over the tips of many nails. No one nail receives enough driving force to penetrate the skin.

So we need a way to distinguish this kind of difference between two situations in which equal force is used, and that is pressure: force divided by the area over which it is applied.
Pressure defined
Pressure is force divided by the area over which it is applied. For a given force, if the area is small, the pressure is large. If the area is large, the pressure is small.
$$P = \frac{F}{A}$$
Units of pressure
The SI unit of pressure is the Pascal:
$$1 \; \text{Pa} = 1 \, \frac{N}{m^2} = 1 \, \frac{Kg}{m s^2}$$
One atmosphere (atm) is the pressure at mean sea level on Earth,
$$1 \, \text{atm} = 101,325 \, Pa.$$
Pounds per square inch (psi) are still commonly used in science and industry in the U.S.
$$1 \, \text{atm} = 14.7 \, \text{psi.}$$
The torr is an older, but still commonly-used unit of pressure. 1 torr is the amount of pressure it takes to raise a column of liquid mercury by 1 mm.
$$760 \, \text{torr} = 1 \, \text{atm.}$$
Because of this, 1 torr is also called "1 mm Hg."
The pressure of Earth's atmosphere in Pascals is a little awkward.
$$1 \text{ bar} = 100 \, KPa$$
is a nicer unit that's often used to measure atmospheric pressure, and it's within 2% of an atmosphere at mean sea-level.
Pressure of a gas
Gases are gases because the atoms and/or molecules that compose them have enough kinetic energy to overcome most of the cohesive forces between them; liquids and solids fly apart. Gas particles completely fill any container we try to put them in.
The animation shows a hypothetical gas particle "filling" its 2-D square container. Gas particles bounce off every wall of the container, and if the sample size is big enough, the total average force of all those collisions with the walls is predictable. The sum of all of those forces over time, divided by the area of the walls is the pressure of the gas.
We can do the calculation using just one wall (say the right wall in the two dimensional animation) if we break the velocity vector of each atom down into x- and y-components. The average of the right-ward x-components at any time divided by the area of the right wall would yield the same pressure.
Move the slider to change the number of atoms in the box between 2 and 20.
Pressure and vacuum
The chamber shown in this photo is a vacuum chamber. NASA uses it to simulate the vacuum of space. When the round door is closed, pumps can be activated to suck all of the gases out to reduce the inside pressure to nearly zero (choose your own pressure unit).

When the pressure inside the vacuum chamber is very low, the pressure outside is still 1 atmosphere (atm). That's because the gases in the atmosphere have mass and are pulled to the surface of Earth by the gravitational force. But gases being gases, these forces press in all directions.
It's interesting to calculate the total amount of force, due to air pressure, on such a door. Comparing it to the size of the people in the photo, the door seems to have a radius of about 3 people, or about 5 meters. It's area is about A = πr2= 75 m2, which is about 800 square feet. Now normal atmospheric pressure is about 14 lbs. per square inch, so at 144 in,2 per ft,2, that's a weight of 14·144·800 = 815 tons of weight. The pressure of a gas can be a powerful force.
Pressure under a liquid
A diver under the surface of the water experiences a pressure due to the weight of all of the water above her pressing down. The deeper she dives, the more water is above her and the more pressure she will feel.
Let's create a cylinder of water with a cross sectional area that is 1 square meter (simply for convenience), and with the height of the water above the diver of $h$.

Now the volume of such a cylinder, in cubic meters is just $h$ if $h$ is in meters.
$$V = h$$
The mass of water is 1 g per $cm^3$ (ml), or 1 Kg per liter. And because there are 1000 liters in every cubic meter, the mass of the water in our cylinder is
$$m = 1000 \frac{Kg}{m^3} V$$
Now the force of that mass (its weight) pushing down on the diver is that mass multiplied by the acceleration of gravity, $g = 9.81 \, \frac{m}{s^2}$, which gives us a force, in Newtons, of
$$F = ma = 9800 \; N$$
This force is equal to the pressure because we chose an area of 1 m2. Here are some typical pressures that a diver would experience at depths between 1 and 100 meters below the surface of the water.
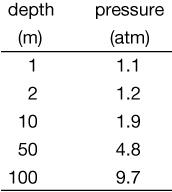
Notice that 1 atm has been added to each result because the air, and it's weight is still up there. The pressure due to the water is in addition to the air pressure we all live under all the time.
You might notice from the figure, and you might also have some experience with this, that the bubbles that a diver exhales expand as they rise. That's because the pressure pushing in on them from the outside is lower as they rise. It's the same thing with bubbles that form in the bottom of a glass of soda and rise. They expand a little.
Only the height of the column of water is relevant in calculating pressure. In the example above, if the circular area of the cylinder were doubled, the mass would be doubled, too, and the two effects would cancel, yielding the same pressure.
Example 1
Glacial ice has an average density of $850 \; Kg·m^{-3}.$ Calculate the pressure, in atmospheres, of 50 m of glacier ice on the rock below it.

The volume of such a chunk of ice would simply be the height in meters, therefore we're working with a sample of ice of volume 50 m3, and mass
$$ \begin{align} m &= 850 \; \frac{Kg}{m^3} \cdot 50 \; m^3\\[5pt] &= 42,500 \, Kg \end{align}$$
The force of gravity on this mass of ice is
$$ \begin{align} F = mg &= (42,500 \, Kg)\left( 9.8 \, \frac{m}{s^2}\right) \\[5pt] &= 416,500 \; N \end{align}$$
Because the area is 1 m3, the pressure in Pascals is 416,500 Pa, and here is that pressure in some other units.
$$ \begin{align} P &= 416,500 \; Pa \\[5pt] &= 4.1 \; atm \\[5pt] &= 60.4 \; psi \end{align}$$
These forces account for the inexorable, slow, grinding force of glaciers on rock, capable of carving deep valleys and moving ground-up rubble like a bulldozer over the eons.
Measuring pressure — The liquid manometer
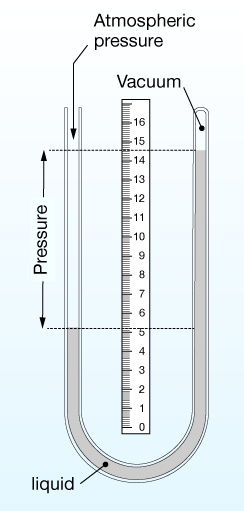
A very common (if a bit old-fashioned) method of measuring pressure is the liquid manometer. The liquid can be any substance, but mercury (Hg) was used often.
The device is a U-shaped tube, sometimes closed at one end after creation of a vacuum there, for a pressure of zero: P = 0. (Note that zero pressure is really hard to achieve. In practice such vacuums have pressures of a millitorr (10-6 atm.) or so.)
In the device illustrated here, any pressure on the open (left) side of the tube will push the liquid down. We can measure the difference between the column heights to calculate that pressure.
$$\Delta P = \rho g h,$$
where $\rho$ (Greek letter "rho") is the density of the liquid, $g$ is the acceleration of gravity on Earth ($g = 9.81 \, m/s^2$), and $h$ is the difference in heights of the columns.
A look at the units of this equation can be helpful:

Now the SI units of pressure are Newtons/m2 (N/m2), where $1 \, N = 1 \, Kg\cdot m/s^2$. We can show therefore, that the units above are indeed those of pressure in SI units.
$$\frac{N}{m^2} = \frac{\frac{Kg\cdot m}{s^2}}{m^2} = \frac{Kg}{m\cdot s^2}$$
It's also worth noting that the diameter of the tubing doesn't matter, only its height.
In the case where we have vacuum on one side of the manometer, ΔP is the absolute pressure on the other side. This kind of manometer is often used to measure atmospheric pressure. The pressure of the atmosphere at sea level on Earth averages 760 mm of Hg, or 760 torr.
Studying extremely high pressures
In the laboratory, it is possible to study extremely high pressures. A typical way to do that is the so-called "diamond anvil cell," shown here.
The small sample (red rectangle) is captured between the sharp points of two diamonds. Those diamonds are carefully aligned to avoid the points slipping past each other, and then screwed together. The pressures involved can be tremendous because
The cross-sectional area of the applied force is very small – the size of the pointed end of a diamond, and
Diamonds are very difficult to deform or crush. They are one of the hardest substances of which we know, so all of the force is transmitted to the sample.
Pressures in excess of 7-million atmospheres have been generated with diamond anvil cells.

SI units
SI stands for Système international (of units). In 1960, the SI system of units was published as a guide to the preferred units to use for a variety of quantities. Here are some common SI units
| length | meter | (m) |
| mass | Kilogram | (Kg) |
| time | second | (s) |
| force | Newton | N |
| energy | Joule | J |
Practice problems
-
A vacuum chamber has an opening (a "port") with a diameter of 24 cm, fitted with a rubber O-ring that seals to a flange that covers the port. If the pressure outside the chamber is 1 atm., and a vacuum of 200 mtorr (1000 mtorr = 1 torr) is produced inside of the chamber, calculate the total force holding the flange in place.

Solution
The total amount of pressure pushing from the outside to the inside is just the difference in external and internal pressures. In this case, it's $760 \, torr - 0.2 \, torr,$ which is approximately 760 torr or 1 atm. Now
$$P = \frac{F}{A} \: \color{#E90F89}{\longrightarrow} \: F = P \cdot A$$
Now let's convert the pressure (1 atm) to a unit that will give us a familiar force: 1 atm. = 17.4 psi. The area of the flange is $A = \pi r^2 = \pi \cdot 4.72 \, in = 14.84 \, in^2.$
$$ \begin{align} F &= (14.7 \, lb) \cdot (14.84 \, in^2) \\[5pt] &= 218 \, lb. \end{align}$$
The flange is being held on with the force of a 218 lb. person standing on it.
-
The density of fresh water is about 1000 Kg/m3, and that of ocean (salt) water is about 1024 Kg/m3. Calculate the pressure on a diver 10 m below the surface in both fresh and salt water.
Solution
We'll let our area be 1 m2, so the volume of the water column above will be 10 m3. Now the masses of the fresh and saltwater are:
$$ \begin{align} m_{\text{fresh}} &= 10 \, m^3 \cdot \frac{1000 \, Kg}{m^3} \\[5pt] &= 10,000 \, Kg \\[8pt] m_{\text{salt}} &= 10 \, m^3 \cdot \frac{1024 \, Kg}{m^3} \\[5pt] &= 10,240 \, Kg \end{align}$$
The resulting forces are (F = ma):
$$ \begin{align} F_{\text{fresh}} &= \:98,000 \, N \\[5pt] F_{\text{salt}} &= 100,352 \, N \end{align}$$
Dividing each of those forces by 1 m2 gives the pressure in Pascals. The pressure is about 2.4% greater in salt water because of the increased density.
-
A vertical tube with a radius of 1 cm and a top open to the atmosphere contains (by height on the tube) 3 cm of oil (density $\rho_{oil} = 0.80 \rho_{water}$) floating on top of 2 cm of water. Calculate the gauge pressure (defined as the pressure in excess of atmospheric pressure) at the bottom of the tube.
Solution
We'll take the density of water to be 1000 Kg/m3. Only the depth and weight of the fluids matter, so
$$ \begin{align} p &= \rho_{oil} \cdot g \cdot h_{oil} + \rho_{water} \cdot g \cdot h_{water} \\[5pt] &= 820 \frac{Kg}{m^3} \left( 9.81 \frac{m}{s^2}\right)(0.03 \, m) +\\[5pt] &\phantom{00000} 1000 \frac{Kg}{m^3} \left( 9.81 \frac{m}{s^2}\right)(0.02 \, m) \\[5pt] &= 241.33 + 196.2 = 437.5 \, Pa \end{align}$$
-
A diver wished to descend to a depth of 40 meters. Given that the density of salt water is about 1020 Kg/m3, what pressure will the diver read on his pressure gauge? Convert your answer to atmospheres, too.
Solution
The pressure depends on the depth (h for height of the water column) and the weight of the water, which is given by its density multiplied by the depth:
$$ \begin{align} P &= \rho \, g \, h \\[5pt] &= \left( 1020 \, \frac{Kg}{m^3} \right) \left( 9.8 \, \frac{m}{s^2} \right) (40 \, m) \\[5pt] &= 400,248 \, Pa \end{align}$$
One atmosphere of pressure is 101,325 Pa, so this pressure is roughly four times atmospheric pressure. We should remember that this is a gauge pressure. Pressure gauges are generally set to zero at an atmospheric pressure of 1 atm., so the total pressure on the diver is roughly five atmospheres.
-
A 0.5 Kg hammer head is dropped from a height of 30 cm onto the head of a nail with a head area of 10 mm2. Calculate the pressure exerted by the hammer on the nail head, and the pressure exerted by the point of the nail (area = 0.1 mm2) on a piece of wood.
Solution
This problem is a little tricky. In order to to find the force with which the hammer hits the nail, we have to do it from the momentum perspective. When the hammer hits the nail, we'll assume that it bounces off, so the total momentum change is twice the momentum of the hammer head.
The time it takes the hammer to fall is
$$t = \sqrt{\frac{2d}{g}} = \sqrt{\frac{2(0.3) \, m}{9.81 \, m/s^2}} = 0.247 \, s$$
Now the velocity of the hammer after having fallen 30 cm is
$$v = gt = 9.81 \frac{m}{s^2} (0.247 \, s) = 2.42 \, m/s$$
Now the momentum is
$$p = mv = 0.5 \, Kg (2.42 m/s) = 1.21 \, \frac{Kg m}{s}$$
The momentum change is twice the momentum, so it's $\Delta p = 2.42 \frac{Kg m}{s^2}.$ Finally, the force on the nail is
$$F = \frac{\Delta p}{\Delta t} = \frac{2.42 \, Kg m/s}{0.001 \, s} = 2,420 \, N,$$
where we've assumed that the hit occurs in about a millisecond (0.001 s), probably not a bad assumption. Finally, the pressures on the head and point are
$$ \begin{align} P_{head} &= \frac{F}{A} \\[5pt] &= \frac{2420 \, N}{1 \times 10^{-5} \, m^2} \\[5pt] &= 2.52 \times 10^{8} \, Pa \end{align}$$
$$ \begin{align} P_{point} &= \frac{F}{A} \\[5pt] &= \frac{2420 \, N}{1 \times 10^{-7} \, m^2} \\[5pt] &= 2.52 \times 10^{10} \, Pa \end{align}$$
Cohesive forces
Cohesive forces are the forces between atoms and molecules that cause them to be attracted toward each other, to clump into liquids and solids. These forces are all due to the arrangement of electrons around atoms and atoms bound together in molecules, and work at a relatively long range. At much shorter range, repulsive forces between electron clouds are more important.
The Greek alphabet
| alpha | Α | α |
| beta | Β | β |
| gamma | Γ | γ |
| delta | Δ | δ |
| epsilon | Ε | ε |
| zeta | Ζ | ζ |
| eta | Η | η |
| theta | Θ | θ |
| iota | Ι | ι |
| kappa | Κ | κ |
| lambda | Λ | λ |
| mu | Μ | μ |
| nu | Ν | ν |
| xi | Ξ | ξ |
| omicron | Ο | ο |
| pi | Π | π |
| rho | Ρ | ρ |
| sigma | Σ | σ |
| tau | Τ | τ |
| upsilon | Υ | υ |
| phi | Φ | φ |
| chi | Χ | χ |
| psi | Ψ | ψ |
| omega | Ω | ω |

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.