Potential vs. potential energy – a subtle difference
Electric potential energy is, like gravitational PE, an energy of position, but it also depends upon the charge of the particle in question, so it's not quite the potential energy we're used to. Thus, we refer to it as "potential," and later usually as "voltage."
Electric potential is defined as the potential energy of a particle divided by its charge. Therefore a +2 Coulomb (C) charged particle at one location in an electric field has half the potential as a +1 C particle at the same location.
$$V = \frac{PE}{Q}$$
We define potential that way because the magnitude of the charge also influences the potential energy.
Now recall the equivalence of work & potential energy (and kinetic energy) in a system, so we also have that the potential (V) is the work done in moving a charge through a distance:
$$V = \frac{w}{Q} = \frac{F\cdot d}{Q}$$
These relationships will allow us to calculate the force on a charge based upon where it rests in an electric field. Remember that potential energy is the energy of position, so it changes depending on the position of a charged particle in a field.
Let's backtrack a bit and talk about why things move and develop the idea of a force field.
Electric potential
The electric potential (just "potential" if we understand the context to refer to electric charges) is the potential energy (PE) of a charged particle divided by its charge (Q):
$$V = \frac{PE}{Q}$$
The units of potential are Volts (V), 1 V = 1 Joule/Coulomb (J/C).
Digression: How things move
Nothing moves in the universe unless one of two things are true:
- An object is acted upon by a contact force, like a foot kicking a soccer ball (notice the distortion of that ball — that's cool) or
- An object is subject to a gradient in an invisible force field, like a gravitational field or an electric field.
In the upper photo, the ball will experience a momentary force, but after it loses contact with the foot, it can receive no more force from it, and it continues on only under the forces of gravity and air friction.
Other forces work at a distance, like gravity or electrostatic attraction or repulsion. Think about the attraction or repulsion between two magnets. They don't have to touch to exert forces on each other, but we can say that there's a force field between them. However, there can be no movement unless the forces acting on an object are unbalanced – greater or smaller in one direction than another.
In the case of the skydiver, he falls because the gravitational force is weaker above him than below. That is, he follows the slope or gradient of gravitational strength as he falls. If the skydiver were the same distance from two planets with equal mass (called the Lagrangian point), there would be no net force on him (the pulling forces would be balanced) and he wouldn't move.

Movement in an electric field
Consider a simple electric field formed by charging two parallel metal plates, one positively and the other negatively, as shown below:

Now we take a "test charge," typically a particle of charge +1, and move it around in the field. The test charge is a thinking device – a handy theoretical way to think about motion and forces in fields.
Now if we move the test charge toward the positive side of the field, it will feel repulsion from the positive plate and attraction to the negative plate, so this will be an "uphill" trip, requiring work to be done.
The work will be equal to the potential energy gained, but recall that the force of moving any charge will be multiplied by the charge of any particle.
Ours is a +1 charge, but a +2 charge would feel twice the repulsion and attraction of the +1. We put everything on the same scale by dividing by the charge to get electric potential (V).
Now consider a similar situation, except this time we move the +1 test charge "downhill" toward the negatively-charged plate. We would expect it to accelerate, gaining kinetic energy in exact proportion to the potential energy lost, according to the principle of conservation of energy.

Because $V = PE/Q,$ we have $PE = QV$ or
$$\Delta PE = Q\Delta V.$$
Ground
Potential is a relative term – potential compared to what? When we talk about the electric potential we're always talking about the potential difference between two points, separated by some distance.
Often, the point of comparison is "ground." We view Earth as an infinite source or sink (willing acceptor) of electrons, and its potential is stable. We refer all electrical activity to Earth or "ground" as being of zero potential, or V = 0.
The British call ground "Earth" and speak of whether an electric circuit is "Earthed" rather than "grounded."
We compare most potentials to ground. In an American home, power outlets operate at a potential of about 110 Volts above the ground potential. Homes generally have two sources of potential relative to ground, ±110 V, and we can also tap the potential across these two, for a total potential difference of 220 V.
A battery is ungrounded, and the positive terminal of a 1.5V battery is 1.5V higher than the potential of the negative terminal. We could, of course, ground the negative terminal to make 0V the reference potential of the battery.
An electrical system or circuit doesn't have to be grounded. A motor, for example, will work just fine as long as it can be hooked up to or "across" a certain potential difference, like 24 V. Often, grounding is a safety feature. Accidental (and possibly lethal) electric current will flow more easily to ground than through a human body, so grounding can protect against electrocution.
The symbol for ground in electrical circuits is

Home wiring and grounding
A typical U.S. home electrical service box
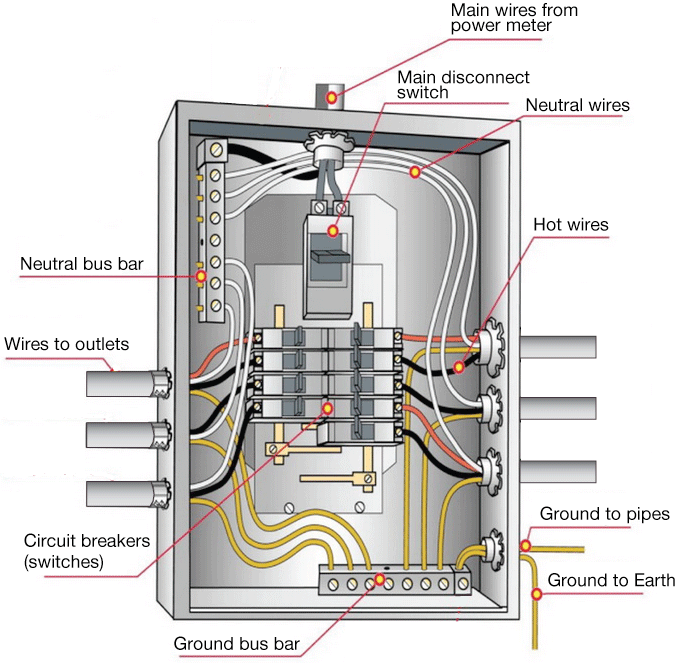
In the U.S., home power is delivered by three wires from a power pole or underground conduit. The voltages are typically ±110 V and a neutral wire, which is grounded to Earth in the system. With such a system, homes can deploy either 110V power (the potential difference between the 110V lines and neutral) or 220V, the potential across ±110 V.
The ±110V wires enter the breaker box at a switch, so that the whole house can be shut down if needed by disconnecting them. They then are connected to a "bus bar," a common connection that in turn connects to a bank of switches (circuit breakers) that can be popped into place.
Circuit breakers are capable of sensing when an unsafe amount of current is flowing and automatically disconnecting the circuit.
Three-wire cables leading to household outlets, lights &c., enter the service box. Their neutral wires are all joined with the supply neutral on a neutral bus bar. Connecting all neutrals makes sure that they are all at the same potential. These are usually connected directly to the home ground.
The grounding wires are all connected to their own bus bar and grounded to Earth, usually both to any metal plumbing in the building (which will likely eventually touch Earth) and to a rod buried in or hammered into the ground.
Fields
Here is another look at electric fields and how they create potential differences. Consider the two illustrations below, a positive charge on the left and a negative charge on the right. The set of circles surrounding each are a kind of topographic map describing the force that another charge would feel if placed a certain distance from the central charge. The closer the lines, the greater the force, just like how the steepness of a mountain or valley slope is shown on a topographic map.
In each diagram, I've put in two positive "test charges" with force vectors on each to indicate the direction and relative size of the force they would "feel" because of their position relative to that center charge. The positive charge repels our test charges, and that repulsion is greater the closer they get to it, thus the longer force vectors. The negative charge attracts our test charge, and that attraction increases as we move the test charge closer to it.

Here is a 3-D view of the same two scenarios. Now the strength of the attractive or repulsive force is modeled by the height of the circles. Positive charges are drawn into a potential well created by the negative charge, and they fall down a "hill". The closer a test charge is to the negative charge, the faster it accelerates toward it because the Coulomb attraction scales as the inverse square of the distance between them (Coulomb's law).
The positive central charge presents as a "hill" to our test charges, and it takes work against the potential field to move a test charge toward the center. The slope of the field is called a gradient. The steeper the gradient, the stronger the force. It works the same for gravity; the farther you are from Earth, the less pulling force the planet exerts on you. The analogy with a topographical map is really pretty good.

For charges all of this behavior is modeled by Coulomb's law, an inverse-square law analogous to the universal law of gravitation. Here's a comparison of the two laws, two of the most important relationships in physics:

It's worth comparing these two force laws:
- The constants $G$ and $k$, the universal gravitation constant ($G = 6.674 \times 10^{-11} \, \frac{N m^2}{Kg^2}$) and Coulomb's constant ($8.99 \times 10^9 \, \frac{N m^2}{C^2}$) respectively, are proportionality constants, and you can really think of them as just being there to get the units right.
- In the ULG, we multiply masses; in Coulomb's law it's charges. Notice that mass is always a positive quantity, while charge can be negative or positive. That means that the force between charges can be negative (by convention that's attractive) or positive (repulsive). Recall that like charges repel and opposite charges attract. On the other hand, no one ever suddenly gets ejected from the surface of a planet because gravity becomes repulsive. It's only attractive.
- Notice the sizes of the constants: $10^{-11}$ for $G$ and about $10^{10}$ for $k$. For equal masses that carry equal charge, the Coulomb force (electrostatic force) is about 40 orders of magnitude (40 zeros!) stronger than the gravitational force.
- Both forces are inversely proportional to the square of the distance between bodies, $r$. That means that if the distance between particles is halved, the force increases by a factor of $2^2$ or $4$. If the distance is doubled, the force drops to a fourth of its original size.
Electric fields — dipoles
We just need to do a little more thinking about electrostatic forces and electric fields before we can really understand electric potential.
Here is a rendering of the electric field produced by a positive and negative charge moved close enough to affect one another. The arrangement is called a dipole — two "poles," positive and negative, like the north and south poles on a bar magnet.
The blue lines are called electric field lines, or just field lines. They indicate the direction of the electrostatic force that would be experienced by a single hypothetical positive charge called a test charge.
In the lower figure, three locations of our test charge are shown along with vectors representing the forces applied to them. The red vectors represent the repulsive force of the positive pole. Note that the red vectors are longer (representing a stronger force) because the test charge is closer to the positive pole, and they always point away from it. Likewise, the black vectors are the attractive forces due to the negative pole. The blue vector is the sum of these for each location, the net force on the test charge. These net force vectors form the field lines an give us their direction.

We use the test charge method to map out all electric fields, and we draw in the resulting field lines so that they're close together where the force is high, farther apart where it is low.

Gradients
Finally, let's look at a 3D view of that dipole we discussed above. The bottom axis represents the position of the test charge along the axis connecting the two charges. The right axis represents position at a 90˚ angle to that, and on the vertical axis we plot the force; up is repulsive, and down is attractive. This plot makes clear the force felt by our test charge and how it would move if we placed it somewhere and let go.
The blue areas of the plot are fairly flat, so the test charge would accelerate (remember that forces produce acceleration, F = ma) only slowly if placed in those regions. Other regions are steep. We say that there is a steep force field gradient in these regions, and the test charge would accelerate rapidly there.

Force field gradients accelerate particles. If there is no gradient, there is no net force, so there can be no acceleration. The steeper the gradient, the greater the acceleration.
"Voltage" ... or how lousy language persists
This is more of a peeve of mine than anything else: I don't like how we append the suffix "age" onto words to make them mean what can be better expressed by another perfectly fine word. When we say "voltage" we really mean electric potential. When we say "square footage" we really mean "area", and when say "percentage" we really mean “fraction” (which can be expressed as percent).
Oh, and never, ever say "amperage" when you mean current or "ohmage" when you mean resistance. That's strictly bush-league.

Fields and calculus
The force on a particle (particle is a generic word for "object" in physics) in a force field is the slope of the field or potential energy function in some direction. When potential energy functions get more complicated, like the mock-2D potential below, we generalize that concept of slope to the gradient, slope that has to be specified by more than one direction.
For a function f(x) of one variable, the slope is given by
$$\frac{df}{dx}$$
For functions of two variables, we use the gradient operator, given the symbol ∇ ("nabla"), often read "grad".
$$\nabla f(x, y) = \frac{df}{dx} \hat{i} + \frac{df}{dx} \hat{j}$$
In this equation the derivative of the 2D function with respect to x is taken by treating y like a constant. Likewise, the second term is the derivative of the 2D function with respect to y, treating x like a constant. i and j are unit vectors in the x- and y-directions, respectively. More properly, we should write partial derivative symbol ∂ instead of d.
$$\nabla f(x, y) = \frac{\partial f}{\partial x} \hat{i} + \frac{\partial f}{\partial x} \hat{j}$$
The gradient operator is easily generalized to any number of dimensions. Even though you might not be able to conceive of them, many problems are solved in many more than three dimensions.
The figure below shows a 2D function with a gradient field below it. Each arrow in the gradient field indicates the direction and magnitude of the slope at that location. In this figure the arrows point up-slope.

Ohm's law and the flow of current
In most applications of electricity, what we're really interested in is regulating the flow of electric current to do useful things. We'd like to make the flow of current predictable and to be able to manipulate it.
It turns out the the flow of current through a material is directly proportional to the potential, and it's inversely proportional to the resistance of the material to the flow of current. That's known as Ohm's law, and it's written like this:
Ohm's law is one of the most important relationships in all of the field of electricity and magnetism.
$$I = \frac{V}{R}$$
If we want more current, we can either
- increase the potential (voltage) or
- decrease the resistance.
Later you will see electric circuits in which the potential, current and resistance are fixed, and those in which each can depend upon other things, such as frequency of switching current on and off. All of this leads to all of the wonderful electronic devices to which we've become so accustomed.
Ohm's law is usually written on one line as a product, $V = IR$.
Ohm's law
Ohm's law: Potential is current multiplied by resistance.
$$V = IR$$
Electric "pressure"
In and electric circuit, electric potential or voltage can be thought of as providing electric pressure on charge carriers (like electrons). The higher the voltage, the more pushing force charge carriers receive. Thus, high voltages will, in general, produce higher currents.
Example 1
How much work is required to move a -2.0 μC charge from ground (0.0 V) to a position where the potential is +60V ?
$$V = \frac{w}{Q} \; \longrightarrow \; w = VQ$$
Plugging in the potential, V = 60 V and the charge, $2.0 \times 10^{-6} \, C$, we have:
$$ \begin{align} w = VQ &= (60 \; V)(2 \times 10^{-6} \; C) \\[5pt] &= 1.2 \times 10^{-4} \; J \\[5pt] &= 120 \; \mu J \end{align}$$
Notice also that the product of Volts and Coulombs is Joules.
Example 2
The work to move a charge of 1.0 μC from point A to point B is 4.5 × 10-4 J. If the particle started from rest and has kinetic energy, KE = 1.2 × 10-4 J at point B, what must the potential difference be between point A and point B ?
$$ \begin{align} V &= \frac{w}{Q} = \frac{4.5 \times 10^{-4} \; J}{1 \times 10^{-6} \; J} \\[5pt] &= 450 \; V \end{align}$$
Now we actually did more work than necessary, because we accelerated the particle so that it has excess kinetic energy, $KE = 1.2 \times 10{-4} \, J$.
We'll want to subtract that much energy from our work to get the potential:
$$ \begin{align} V &= \frac{KE}{Q} = \frac{1.2 \times 10^{-4} \; J}{1 \times 10^{-6} \; J} \\[5pt] &= 120 \; V \end{align}$$
So the potential difference is
$$450 \; V - 120 \; V = 330 \; V$$
gradient
An increase or decrease in the magnitude of some property like force or temperature observed in passing from one point or moment to another.

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.