Here are a couple of examples of interesting results that come out of a trigonometric analysis when either the sine or cosine function ends up in the denominator. Remember that sin(θ) or cos(θ) can equal zero, so the graph of any function that has either in the denominator will include vertical asymptotes. Physically, this means that a force represented by a vector in a function can be infinitely large in the right circumstances.
Take a look at the rock climbing example below. When setting up a rock-climbing anchor, one wants always to have some redundancy — more than one anchor, and to share the load (e.g. of a falling person) among two or more anchors (we'll just use two in this analysis).
Take a look at the vector diagram for our anchor. The angle θ in the diagram is the angle between the anchors. Each anchor shares some fraction of the downward load. But that share is only one-half of the load if θ = 0˚. Otherwise, the tension in each of the anchor "arms" gets larger as θ grows.
The forces in each of the two anchor arms (we'll assume they're the same for simplicity) is the sum of vector forces in the up—down and left—right directions. The left-right forces cancel at equilibrium,
$$F_{2x} = -F_{1x}$$
so the upward forces (F1y and F2y) must equal the normal force, FN.
$$F_N = F_{1y} + F_{2y}$$
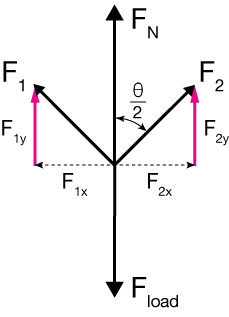
Now the tension in anchor 2 is $F_2$, and we can relate $F_{2x}$ to $F_{1x}$ using the cosine function:
$$cos \left( \frac{\theta}{2} \right) = \frac{F_{2y}}{F_2}$$
Solving for the tension, $F_2$, gives
$$F_2 = \frac{F_{2y}}{cos\left( \frac{\theta}{2} \right)}$$
Notice that the tension is inversely proportional to θ/2, wo when θ = 0, the tension is $F_{2y}$, but when θ → 180˚, the cosine of θ/2 is zero and the tension in the right arm is infinite.
The tension in each arm of an anchor system like this approaches infinity as the angle between the two approaches 180˚C.
This analysis shows that it will pay to keep the angle between your climbing anchors as close to zero as possible in order to minimize the actual force applied to each anchor point. Those forces can multiply dramatically during the downward acceleration of a falling climber.
This graph shows that as the angle θ approaches 180˚ any function inversely proportional to [cos(θ/2)]> grows infinitely as θ → ∞.
Our rock-climbing example has a lot of other implications. For example, think about overhead wires like the power and communicaion wires likely strung through your neighborhood. Notice that all of them sag just a bit.
If you think of one span of these wires forming a climbing anchor, with each pole as an anchor point and an invisible load in the middle of the wire (representing the weight of the wire itself), you can see that it would take an infinite amount of tension in the wire in order not to have a bit of sag. It's impossible to get rid of that sag. Even the tightest cable strung between the most solid anchors will sag just a little. Even a guitar string sags just a little under the force of gravity, it's just very light and doesn't sag a noticable amount.
The shape of a sagging cable, rope or chain, which looks a bit like a parabola, is actually a catenary curve. I will describe catenary curves in more detail if I ever find the time!
Dr. Cruzan's Math and Science Web by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.
