Our first look at curved functions
Quadratic functions are usually the first we encounter that have curved or nonlinear graphs. The graph of a quadratic function is a specific kind of curve called a parabola, a sort of U-shaped figure.
All quadratic functions include a term that contains the square of the independent variable, like $x^2.$ There can be no higher power of $x$ in a quadratic function. Some examples are
$$ \begin{align} f(x) &= 2x^2 - 3x + 1 \\[5pt] f(x) &= (x - 4)^2 \\[5pt] f(x) &= -x^2 - 71 \end{align}$$
Quadratic functions have the general form
$$f(x) = Ax^2 + Bx + C$$
where $A$, $B$ and $C$ are fixed numbers (constants) that don't change, and the highest power of the independent variable $(x)$ is 2.
Notice that in $Ax^2 + Bx + C,$ the x in the second term has an exponent of 1; we just aren't in the habit of writing those "invisible" 1's.
The parent function of all quadratic functions is the simplest, with $A = 1, \; B = C = 0,$ $f(x) = x^2.$
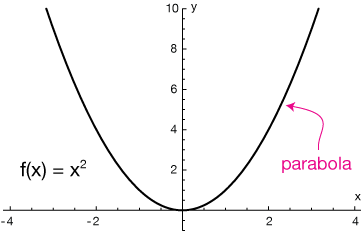
* Pro tip:
Not all U-shaped graphs are parabolas. The parabola is the unique graph of a quadratic function. Even something like a hanging cable or rope isn't really a parabola (it's a catenary), though it's pretty close.
Quadratic functions are very important. There's a lot to cover, so the material is broken up into sections.
- This section deals with definitions, the the form of the graphs of parabolas and their transformations of those graphs.
- Solving quadratic equations covers all methods of solving quadratic equations for x.
- Quadratic applications covers various kinds of problems you can solve using quadratic functions.
Form of a quadratic function
The basic or general form of a quadratic function is shown below, where $A$, $B$ and $C$ are fixed, numerical constants, and where $B$ or $C$ can be zero. If $A = 0$, of course, there is no $x^2$ term and it's not a quadratic. Terms with $x$ to the first and zero powers are shown, but in practice we write $x^1 = x$ and $x^0 = 1$ (which is not written at all - the ghost 1).

The form is usually written like this,
$$f(x) = Ax^2 + Bx + C$$
and we can find other clever ways to disguise it.
Anatomy of a Parabola (vocabulary)
Here are graphs of two parabolas. Use them to learn the terminology we'll use when referring to graphs of curved and parabolic functions.
A parabola is characterized by its vertex (the lowest or highest point of the graph – the bottom or the top), by the direction in which it "opens" — up or down, and by the steepness of the rise of its ends. The ends can rise or fall very steeply or the graph can be very shallow — or anything in between.
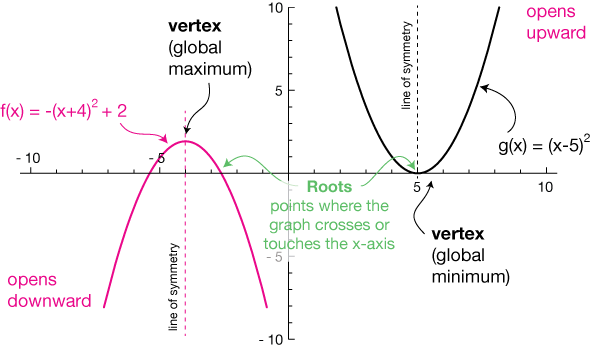
The vertex of any parabola is either a global maximum (highest point) or a global minimum (lowest point). It's the point where the slope of the curve (which we define as the slope of the line tangent to the curve at the point of interest) switches from + to - or - to +. The vertex of a parabola can be anywhere in the x-y plane.
All parabolas have an axis of symmetry that passes vertically through the vertex. Either side of the parabola is the mirror image of the other across that line. That kind of symmetry is called reflection symmetry.
The roots of a quadratic function (or any function) are the points where it crosses the x-axis, where $f(x) = 0.$ Strictly-speaking, a quadratic function always has two roots, but they might not be real numbers. A parabola can touch the x-axis just once, as on the right above (a "double root"), twice as on the left (two real roots), or not at all, in which case the roots are "imaginary" and can't be plotted on an x-y graph. More on those later.
The function $f(x) = x^2$ is called an even function because $f(-x) = f(x);$ for example, $f(-2) = f(2) = 4.$
Transformations
Translations & the vertex form
By applying the horizontal and vertical translation transformations we learned in the functions section, we can derive what we call the vertex form of the quadratic function:
$$f(x) = A(x - h)^2 + k ,$$
where $A$ is the vertical scaling parameter and $(h, \, k)$ is the vertex (It's called the vertex form because the coordinates of the vertex embedded in it are obvious). If we expand this (expand means to carry out the squaring of the binomial and distribute the $A$), we get

Notice the correspondence between the coefficients of the standard form of the quadratic equation: $A = A$, $B = -2Ah$ and $C = Ah^2 + k$. It is from the correspondence for $B$ that we arrive at an easy formula for the $x$-coordinate of the vertex of a parabola:
x-coordinate of the vertex:
$$h = \frac{-B}{2A}$$
The y-coordinate is then easily found by plugging $h$ in to the function to get $y = f(h)$. Remember that that's what functions are for — you put in an $x$ to get the $y$ that goes with it in $(x, y)$. You should memorize the formula for the x-coordinate of the vertex. You'll need to use it quite a lot to solve problems: $h = -B/2A$.
Video 2 below shows you how to convert between standard and vertext form.
Vertex form of a quadratic
The vertex of a parabola $(h, k)$ is obvious if the function is written in vertex form
$$f(x) = A(x - h)^2 + k$$
and if it's written in standard form, $f(x) = Ax^2 + Bx + C,$ the x-coordinate of the vertex is $x = -B/2A.$
Transformations: vertical translation
When we simply add or subtract a constant to/from the end of a function (the $k$ in the vertex form in the box above), the effect on the graph is to raise or lower the whole graph by $k$ units.
Manipulate the slider on the graph to change $k$ in
$$f(x) = x^2 + k$$
If $k$ is negative, the translation is downward, and if $k$ is positive the translation is upward.
Notice that $f(x) = x^2 + k$ is just $f(x) = x^2,$ our parent function, with $k$ added to every $y$ value it produces. The vertical translation is probably the easiest transition to understand, and it works exactly the same way in any function.
Transformations: horizontal translation
When we subtract a constant, $h,$ from the independent variable of any function $(x - h),$ the effect is to translate it left or right (See the functions page to brush up on this). If $h \lt 0,$ the translation is to the left, and if $h \gt 0$ it's to the right. Note that we subtract $h$ from $x$ before squaring (PEMDAS!).
Recall that this "feels" backward: $(x - 2)^2$ is a $x^2$ shifted two units to the right, and $(x + 2)^2$ is a $x^2$ shifted two units to the left, because it's really $(x - (-2))^2.$ Notice that on when $x$ is negative, we're subtracting a negative number inside the parenthesis: $(x - -h) = (x + h).$
Move the slider around on the graph to see the effect of changing $h.$ Notice what happens when $h$ gets bigger in both the positive and negative directions.
Combined translations
In this example, horizontal and vertical translations of 2 units in the positive direction are combined. We can do this sort of thing in exactly the same way for any function at all. More things are the same in mathematics than different!
The function looks like
$$f(x) = (x - h)^2 + k$$
where $h$ is the horizontal translation and $k$ is the horizontal translation. That means that the vertex of such a parabola is $(h, k)$. Here's an example of a parabola that's just the parent function, $f(x) = x^2$ shifted 2 units to the right and 2 units upward.

Transformations: Vertical scaling
When we multiply a function by a constant, $A$, the effect is to scale (expand or shrink) the graph vertically. If $A \gt 1$, the function is stretched vertically. If $A \lt 1$ it is compressed vertically, and if $A$ is negative, it still scales the graph by $|A|$, but it is also flipped across the x-axis. For example, $f(x) = x^2$ has a vertex of $(0, \, 0)$ and opens upward, but $g(x) = -x^2$ opens downward — but has the same vertex.
Move the slider back and forth to change the value of the $A$ parameter and watch its effect on the function.
Transformations: Horizontal scaling
When we divide the independent variable of a function by a constant number, $c$, the effect on its graph is horizontal scaling (stretching or compressing). For example, if $x$ is divided by a number greater than 1, the graph is stretched horizontally. If it's divided by a number less than 1 (like ¼; in the plot here) the graph is compressed horizontally.
Move the slider back and forth to see the effect of the parameter c on the function. Notice that horizontal stretching looks a lot like vertical compression, and horizontal compression looks a lot like vertical stretching.
Combining the four transformations
As with all functions, all of the various transformations can be combined for quadratic functions. Starting with the parent function, we can form any quadratic like this:

Transformations
These transformations apply to any kind of function, and they always do the same things. Learn them now so that you'll easily be able to apply and interpret them with the other functions you'll learn along the way.
$$f(x) = A \left( \frac{x}{c} - h \right)^2 + k$$
A cautionary note about scaling
We have to be careful about the effect of horizontal scaling when we look for the vertex of a quadratic function.
Here's a quadratic that looks like it's stretched by a factor of two in the horizontal direction (accomplished by dividing the independent variable $(x)$ by 2 where it occurs inside the function), and has a vertex of (2, 3).
$$f(x) = \left( \frac{x}{2} - 2 \right)^2 + 3$$
It looks like the vertex of this function should be (2, 3), but it's not. If we expand this function to standard $(f(x) = Ax^2 + Bx + C)$ form, we get
$$f(x) = \frac{1}{4} x^2 - 2x + 7$$
Now we can determine the x-coordinate of the vertex using $x = -B/2A$, and it's not 2:
$$\frac{-B}{2A} = \frac{1}{2 \cdot \frac{1}{4}} = 4$$
Plugging 4 into the function gives us the y-coordinate,
$$f(4) = \frac{16}{4} - 8 + 7 = 3$$
which is what we'd expect, $y = 3$. The vertex of this parabola is at (4, 3). So what's going on? That horizontal stretching transformation has moved the vertex horizontally, too. Here's why:

When we multiply the binomial that contains the transformation, that divisor of 2 also contributes to the $B$ term of the function, and therefore affects the x-coordinate of the vertex. Those mixed terms can move the vertex. It's that $2x$ that's moved the vertex from what we'd expected.
$$= \frac{x^2}{4} - \bf{2x} + 4$$
Example 1
You'll need to become very good at quickly sketching quadratic functions. There are many clues about what the graph of a quadratic looks like; here's a first example.
Sketch the graph of $f(x) = 2(x - 3)^2 + 1$
- Translate 3 units to the right (long green arrow)
- Translate 1 unit upward (short green arrow)
- Scale (stretch) vertically by a factor of two. (blue curve)
This moves the vertex of the parabola from $(0, 0)$ to $(3, 1)$. Notice that when a quadratic function is in vertex form, we can easily just "read" the vertex from the function definition. The vertical scaling of 2 has the effect of stretching the parabola upward (by a factor of 2) from the vertex.
Now it's easy to sketch the graph →

It's often very useful to sketch the parent function onto a graph first, then follow the transformations to sketch the new function.
Example 2
Sketch the graph of $f(x) = x^2 + 2x + 1$
The x-coordinate of the vertex is:
$$h = \frac{-B}{2A} = \frac{-2}{2(1)} = -1$$
The we obtain the y-coordinate simply by plugging $x = -1$ into the function:
$$f(-1) = (-1)^2 + 2(-1) _ 1 = 0$$
Now because $A \gt 0,$ the parabola opens upward. It's also easy to find the y-intercept, the point where $x = 0: \; f(0) = 1.$

We'll do more graphing of quadratics below, and that will entail some solving for the roots (f(x) = 0, places where the graph crosses the x-axis, if it does). I've saved that topic for another page, which you might want to skip to now and come back.
Practice problems
A. Sketch graphs of these quadratic functions. Notice that they are all written to make the transformations from $f(x) = x^2$ obvious.
-
$f(x) = (x - 1)^2 + 2$
Solution
$f(x) = (x - \color{magenta}{1})^2 + \color{magenta}{2}$
This function is the parent function, $f(x) = x^2$ shifted to the right by 1 unit and upward by 2 units. So its vertex has moved from $(0,0)$ to $(1, 2)$.
Just to help locate our function, it's easy to calculate the y-intercept: $f(0) = (-1)^2 + 2 = 3$.
Here is a graph of $f(x) = x^2$ and $f(x) = (x - 1)^2 + 2$:

-
$f(x) = x^2 - 2$
Solution
This is just $f(x) = x^2$ shifted downward by 2 units. For graphing purposes, it's easy enough to find the roots of this function:
$$ \begin{align} x^2 - 2 &= 0 \\[5pt] x^2 &= 2 \\[5pt] x &= \pm \sqrt{2} \end{align}$$
Here is a graph of $f(x) = x^2$ (dashed) and $f(x) = x^2 - 2$ (solid):

-
$f(x) = \frac{1}{2}(x + 3)^2 - 4$
Solution
This function is $f(x) = x^2$ with three transformations applied: It is shifted 3 units to the left and 4 downward, moving the vertex from $(0, 0)$ to $(-3, -4)$. It is also scaled vertically by a factor of ½, flattening it out a bit compared to $f(x) = x^2$. Its y-intercept (just for an anchor point for graphing purposes) is
$$ \begin{align} f(0) &= \frac{1}{2}(3)^2 - 4 \\[5pt] &= \frac{9}{2} - 4 = \frac{1}{2} \end{align}$$
Here is a graph of $f(x) = x^2$ (dashed) and $f(x) = \frac{1}{2}(x + 3)^2 - 4$ (solid):

-
$f(x) = (x - 1)^2 + 2$
Solution
The vertex of this parabola is $(1, 2)$, and there are no other transformations. The y-intercept is $f(0) = 1 + 2 = 3$. Here is a graph of $f(x) = x^2$ (dashed) and $f(x) = f(x) = (x - 1)^2 + 2$ (solid):

B. Identify the vertex in each of these quadratic functions. Convert each to standard form, $f(x) = Ax^2 + Bx + C,$ then find the vertex from that form (x-coordinate = $-B/2A$) and confirm that the two are the same.
-
$f(x) = \frac{3}{4}(x - 2)^2 + 4$
Solution
When the function is written in vertext form like this, it's easy to find the vertex — just read it off from the horizontal and vertical transformations. It's $(2, 4)$. Here's how we'd do it the "long way," by restoring the function to $y = Ax^2 + Bx + C$ form:
$$ \begin{align} f(x) &= \frac{3}{4}(x-2)^2 + 4 \\[5pt] &= \frac{3}{4}(x^2 - 4x + 4) + 4 \\[5pt] &= \frac{3}{4}x^2 - 3x + 7 \end{align}$$
Then the x- and y-coordinates of the vertext are
$$ \begin{align} \color{magenta}{x} &: \frac{-B}{2A} = \frac{3}{3/2} = 2 \\[5pt] \color{magenta}{y} &: f(2) = 3 - 6 + 7 = 4 \end{align}$$
-
$f(x) = -2\left(x - \frac{1}{2}\right)^2 - 1$
Solution
When the function is written in vertext form like this, it's easy to find the vertex — just read it off from the horizontal and vertical transformations. It's $\left( \frac{1}{2}, -1 \right)$. Here's how we'd do it the "long way," by restoring the function to $y = Ax^2 + Bx + C$ form:
$$ \begin{align} f(x) &= -2 \left( x - \frac{1}{2} \right)^2 - 1 \\[5pt] &= -2 \left( x^2 - x + \frac{1}{4} \right) - 1 \\[5pt] &= -2x^2 + 2x - \frac{3}{2} \end{align}$$
Then the x- and y-coordinates of the vertex are
$$ \begin{align} \color{magenta}{x} &: \frac{-B}{2A} = \frac{-2}{-4} = \frac{1}{2} \\[5pt] \color{magenta}{y} &: \left(\frac{1}{2} \right) = -\frac{1}{2} + 1 - \frac{3}{2} = -1 \end{align}$$
-
$f(x) = -(x - 4)^2 + 2$
Solution
This function is $f(x) = x^2$ with three transformations applied: It is shifted 4 units to the right and 2 upward, moving the vertex from $(0, 0)$ to $(4, 2)$. It is also flipped across the horizontal line $y = 2$, which contains the vertext (so it opens downward). We can find the vertex coordnates the "long way," too:
$$ \begin{align} f(x) &= \frac{1}{2}(3)^2 - 4 \\[5pt] &= \frac{9}{2} - 4 = \frac{1}{2} \end{align}$$
Here is a graph of $f(x) = x^2$ (dashed) and $f(x) = \frac{1}{2}(x + 3)^2 - 4$ (solid):
$$ \begin{align} f(x) &= -(x-4)^2+2 \\[5pt] &= -(x^2-8x+16)+2 \\[5pt] &= -x^2 + 8x - 14 \end{align}$$
Then the x- and y-coordinates of the vertex are
$$ \begin{align} \color{magenta}{x} &: \frac{-B}{2A} = \frac{-8}{2(-1)} = 4 \\[5pt] \color{magenta}{y} &: -16+32-14 = 2 \end{align}$$
-
$f(x) = -3(x + 2)^2 - 4$
Solution
This function is $f(x) = x^2$ with three transformations applied: It is shifted 2 units to the left and 4 downward, moving the vertex from $(0, 0)$ to $(-2, -4)$. It is also flipped across the horizontal line $y = -4$, which contains the vertext (so it opens downward), and it's stretched vertically by a factor of 3. We can find the vertex coordnates the "long way," too:
$$ \begin{align} f(x) &= -3(x+2)^2 - 4 \\[5pt] &= -3(x^2 + 4x + 4) - 4 \\[5pt] &= -3x^2 - 12x - 16 \end{align}$$
Then the x- and y-coordinates of the vertex are
$$ \begin{align} \color{magenta}{x} &: \frac{-B}{2A} = \frac{12}{-6} = -2 \\[5pt] \color{magenta}{y} &: f(-2) = -3(4)+12(-2)-16 = -4 \end{align}$$
C. Convert each of these quadratic functions to vertex form, $f(x) = A(x - h)^2 + k.$
-
$f(x) = 3x^2 + 2x - 4$
Solution
$$ \begin{align} \frac{-B}{2A} &= \frac{-2}{2 \cdot 3} = -\frac{1}{3} \tag{1}\\[5pt] f\left( \frac{-1}{3}\right) &= \frac{1}{3} - \frac{2}{3} - \frac{12}{3} = -\frac{13}{3} \tag{2} \\[5pt] f(x) &= 3 \left( x + \frac{1}{3} \right)^2 - \frac{13}{3} \end{align}$$
In (1) we calculated the x-coordinate of the vertex, and in (2) we plugged that into the function to get the corresponding y-coordinate.
-
$f(x) = \frac{x^2}{2} + x + 1$
Solution
$$ \begin{align} \frac{-B}{2A} &= \frac{-1}{1} = -1 \tag{1}\\[5pt] f(-1) &= \frac{1}{2} - 1 + 1 = \frac{1}{2} \tag{2} \\[5pt] f(x) &= \frac{1}{2} (x + 1) + \frac{1}{2} \end{align}$$
In (1) we calculated the x-coordinate of the vertex, and in (2) we plugged that into the function to get the corresponding y-coordinate.
-
$f(x) = -2x^2 + 5x - 11$
Solution
$$ \begin{align} \frac{-B}{2A} &= \frac{-5}{-4} = \frac{5}{4} \tag{1} \\[5pt] f \left( \frac{5}{4} \right) &= -\frac{25}{8} + \frac{25}{4} -11 \\[5pt] &= -\frac{25}{8} + \frac{50}{8} - \frac{88}{8} \tag{2} \\[5pt] f(x) &= -2 \left( x - \frac{5}{4} \right)^2 - \frac{63}{8} \end{align}$$
In (1) we calculated the x-coordinate of the vertex, and in (2) we plugged that into the function to get the corresponding y-coordinate.
-
$f(x) = 4x^2 + 2x - 3$
Solution
$$ \begin{align} \frac{-B}{2A} &= \frac{-2}{8} = -\frac{1}{4} \tag{1} \\[5pt] f \left( -\frac{1}{4} \right) &= -\frac{1}{4} - \frac{2}{4} - \frac{12}{4} = -\frac{13}{4} \tag{2} \\[5pt] f(x) &= -2 4\left( x + \frac{1}{4} \right)^2 - \frac{14}{4} \end{align}$$
In (1) we calculated the x-coordinate of the vertex, and in (2) we plugged that into the function to get the corresponding y-coordinate.
More sketching graphs of quadratic functions
It's easy to plot the graph of a quadratic function on a calculator or computer, but being able to do that doesn't guarantee that you'd notice if you keyed something in incorrectly. You will go far if you already have some notion (the more complete the better) of what a function should look like before you ever plot it on a machine.
Pro tip: Anybody can punch a function into a calculator or computer and get a pretty graph. Not just anyone can be sure it's the right graph. Be that person.
Sketching graphs of quadratics
- Find the vertex. First the x-coordinate using $x = -b/2a,$ then the y, using $y = f(x).$
- Find the y-intercept, $f(0).$ At this point, you can make a decision. If the y-intercept is above a vertex that is itself above the x-axis, then there is no way your parabola can ever cross the x-axis, therefore it must have complex roots, and there's no point in finding them - they won't help you sketch the graph.
- If the opposite is true, you need to find the roots in order to mark the x-axis crossings. That can be done by completing the square or using the quadratic formula, or - if you're lucky - by direct factoring.
Example 3
Sketch the graph of a quadratic function with complex roots. Note that complex numbers can't be plotted on a Cartesian graph. Complex roots simply mean that the function does not intersect the x-axis: $f(x) = x^2 - 4x + 5.$
First find the vertex. The x-coordinate is
$$\frac{-B}{2A} = \frac{4}{2} = 2$$
Then the y-coordinate is $f(2)$:
$$f(2) = 4 - 8 + 5 = 1$$
So the vertex is $(2, 1)$. The y-intercept (a very easy point to obtain, and handy for graphing) is:
$$f(0) = 5$$
We can find the roots by setting the function equal to zero and completing the square:
$$ \begin{align} x^2 - 4x + 5 &= 0 \\[5pt] x^2 - 4x &= -5 \\[5pt] x^2 - 4x + 2^2 &= -5 + 4 \\[5pt] (x-2)^2 &= -1 \\[5pt] x &= 2 \pm i \end{align}$$

Just remember that when the roots are imaginary, the function doesn't cross the x-axis. this removes some of the information you'd otherwise have to graph it, but you can always calculate the odd point position here and there to help.
Example 4
Sketch the graph of a quadratic function with real roots. Real roots are actual points at which the graph crosses the x-axis, so they're valuable aids to graphing the function. Remember that because of the symmetry of a parabola, the x-coordinate of the vertex lies right between the two roots (it's the average of the two).
First find the vertex. The x-coordinate is
$$\frac{-B}{2A} = \frac{-1}{2} = -\frac{1}{2}$$
Then the y-coordinate is $f(2)$:
$$f\left( -\frac{1}{2} \right) = \frac{1}{4} - \frac{1}{2} - \frac{12}{2} = -\frac{25}{4}$$
So the vertex is $\left( -\frac{1}{2}, -\frac{25}{4} \right)$. The y-intercept (a very easy point to obtain, and handy for graphing) is:
$$f(0) = -6$$
We can find the roots by factoring:
$$ \begin{align} x^2 + x - 6 &= 0 \\[5pt] (x+3)(x-2) &= 0 \\[5pt] x &= -3, \, 2 \end{align}$$

Practice problems
Sketch a graph of each of these quadratic functions. In working out the solutions, I've solved each for the roots (f(x) - 0). That's covered in another section: quadratic factoring.
-
$f(x) = x^2 - x + 2$
Solution
Find the vertex:
$$\frac{-B}{2A} = \frac{1}{2}$$
$$ \begin{align} f\left( \frac{1}{2} \right) &= \left( \frac{1}{2} \right)^2 - \frac{1}{2} - 2 \\[5pt] &= \frac{1}{4} - \frac{1}{2} - 2 \\[5pt] &= -\frac{9}{4} \\[5pt] \text{vertex} &= \left( \frac{1}{2}, \; -\frac{9}{2} \right) \end{align}$$
y-intercept: f(0) = -2. Given that parabolas have a vertical axis of mirror symmetry passing through the vertex, that's enough information to graph this one, but we can also find the roots. It factors to
$$f(x) = x^2 - x - 2 = (x - 2)(x + 1) = 0$$
Our graph crosses the x-axis at x = -1, 2. Here's a sketch.

-
$f(x) = 2x^2 - 5x - 3$
Solution
$$f(x) = 2x^2 - 5x - 3$$
Find the vertex:
$$\frac{-B}{2A} = \frac{5}{4}$$
$$ \begin{align} f\left( \frac{5}{4} \right) &= 2\left( \frac{5}{4} \right)^2 - 5\frac{5}{4} - 3 \\[5pt] &= \frac{25}{8} - \frac{50}{8} - 3 \\[5pt] &= -\frac{49}{8} \\[5pt] \text{vertex} &= \left( \frac{5}{4}, \; -\frac{49}{8} \right) \end{align}$$
y-intercept: f(0) = -3. Given that parabolas have a vertical axis of mirror symmetry passing through the vertex, that's enough information to graph this one, but we can also find the roots. It factors to
$$f(x) = 2x^2 - 5x - 3 = (x - 3)(2x + 1) = 0$$
Our graph crosses the x-axis at x = -½, 2. Here's a sketch.

-
$f(x) = 5x^2 - 21x - 20$
Solution
Find the vertex:
$$\frac{-B}{2A} = \frac{21}{2 \cdot 5} = 2.1$$
$$ \begin{align} f\left( \frac{21}{10} \right) &= 5\left( \frac{21}{10} \right)^2 - 21\frac{21}{10} - 20 \\[5pt] &= \frac{5 \cdot 21^2}{100} - \frac{21^2 \cdot 10}{100} - \frac{2000}{100} \\[5pt] &= \frac{21^2(-5) - 2000}{100} \\[5pt] &= \frac{-2205-2000}{100} = -42.05 \end{align}$$
y-intercept: f(0) = -20. Given that parabolas have a vertical axis of mirror symmetry passing through the vertex, that's enough information to graph this one, but we can also find the roots by factoring or completing the square. They are $x = 5, \, -\frac{4}{5}$. Here's a sketch of the graph:

-
$f(x) = 3x^2 - 14x - 5$
Solution
Find the vertex:
$$\frac{-B}{2A} = \frac{28}{6} = \frac{14}{3}$$
$$ \require{cancel} \begin{align} f\left( \frac{14}{3} \right) &= 3\left( \frac{14}{3} \right)^2 - 14\frac{14}{3} - 5 \\[5pt] &= \cancel{\frac{14^2}{3}} - \cancel{\frac{14^2}{3}} - 5 = -5 \end{align}$$
y-intercept: f(0) = -5. Given that parabolas have a vertical axis of mirror symmetry passing through the vertex, that's enough information to graph this one, but we can also find the roots by factoring or completing the square. They are $x = 5, \, -\frac{1}{3}$. Here's a sketch of the graph. The dashed curve is $f(x) = x^2$:

-
$f(x) = x^2 - 16$
Solution
This one's pretty easy. The graph is just the parent function, $f(x) = x^2$ dropped down by 16 units ot put the vertex at $(0, -16)$. The roots are $\pm \sqrt{16} = \pm 4$.
-
$f(x) = 4x^2 - 2x - 12$
Solution
Find the vertex:
$$\frac{-B}{2A} = \frac{2}{8} = \frac{1}{4}$$
$$ \require{cancel} \begin{align} f\left( \frac{1}{4} \right) &= \frac{4}{16} - \frac{2}{4} - 12 \\[5pt] &= \frac{1}{4} - \frac{1}{2} - 12 \\[5pt] &= -\frac{1}{4} - \frac{48}{4} = -\frac{49}{4} \\[5pt] &\text{vertex: } \left( \frac{1}{4}, -\frac{49}{4} \right) \end{align}$$
Roots (by completing the square)
$$ \begin{align} 4x^2 - 2x &= 12 \\[5pt] 2x^2 - x &= 6 \\[5pt] x^2 - \frac{x}{2} &= 3 \\[5pt] x^2 - \frac{x}{2} + \left( \frac{1}{4} \right)^2 &= \frac{1}{16} + \frac{48}{16} \\[5pt] \left( x - \frac{1}{4} \right)^2 &= \frac{49}{16} \\[5pt] x = \frac{1}{4} \pm \frac{7}{4} &= 2, \, -\frac{3}{2} \end{align}$$
y-intercept: f(0) = -12. Here's a sketch of the graph. The dashed curve is $f(x) = x^2$:

-
$f(x) = x^2 - 3x + 7$
Solution
Find the vertex:
$$\frac{-B}{2A} = \frac{3}{2}$$
$$ \require{cancel} \begin{align} f\left( \frac{3}{2} \right) &= \frac{9}{4} - \frac{9}{2} + 7 \\[5pt] &= \frac{9}{4} - \frac{18}{4} + \frac{28}{4} \\[5pt] &= \frac{19}{4} \\[5pt] &\text{vertex: } \left( \frac{3}{2}, \frac{19}{4} \right) \end{align}$$
Roots (by completing the square)
$$ \begin{align} x^2 - 3x &= -7 \\[5pt] x^2 - 3x + \left( \frac{3}{2} \right)^2 &= \frac{9}{4} - \frac{28}{4} \\[5pt] \left( x - \frac{3}{2} \right)^2 &= -\frac{19}{4} \\[5pt] x = \frac{3 \pm i\sqrt{19}}{2} \end{align}$$
y-intercept: f(0) = 7. Here's a sketch of the graph. The dashed curve is $f(x) = x^2$:

-
$f(x) = 2x^2 - x + 8$
Solution
Find the vertex:
$$\frac{-B}{2A} = \frac{1}{4}$$
$$ \require{cancel} \begin{align} f\left( \frac{1}{4} \right) &= \frac{2}{16} - \frac{1}{4} + 8 \\[5pt] &= \frac{1}{8} - \frac{2}{8} + \frac{64}{8} \\[5pt] &= \frac{63}{8} \\[5pt] &\text{vertex: } \left( \frac{1}{4}, \frac{63}{8} \right) \end{align}$$
Roots (by completing the square)
$$ \begin{align} x^2 - x &= -8 \\[5pt] x^2 - \frac{x}{2} &= -4 \\[5pt] x^2 - \frac{x}{2} + \left( \frac{1}{4} \right)^2 &= \frac{1}{16} - \frac{64}{16} \\[5pt] \left( x - \frac{1}{4} \right)^2 = -\frac{63}{16} \\[5pt] x &= \frac{i \pm \sqrt{63}}{4} \end{align}$$
y-intercept: f(0) = 8. Here's a sketch of the graph. The dashed curve is $f(x) = x^2$:

Finding the equation of a parabola from three points
Through any three points, only one unique parabola can be drawn. That may be a bit hard to come to terms with at first, but remember that a parabola isn't just any curve. It's a very specific kind of curve, the graph of a quadratic function. We'd like to be able to find the equation of that parabola.

Let's say that a parabola passes through three known points, $(x_1, y_1), (x_2, y_2),$ and $(x_3, y_3).$ Now we know that the general form of the equation we're looking for is
$$y = Ax^2 + Bx + C$$
If each of out three points satisfies this equation for a certain set of A, B and C (the things we're really looking for), we have three equations:
$$ \begin{align} y_1 &= Ax_1^2 + Bx_1 + C \\[4pt] y_1 &= Ax_2^2 + Bx_2 + C \\[4pt] y_1 &= Ax_3^2 + Bx_3 + C \end{align}$$
Now that's three equations and three unknowns (A, B, C), so we should have enough information to determine what they are.
It's probably best at this point to work an example or two, so let's find the equation of the parabola above, which passes through
Here are our three equations:
$$ \begin{align} 8 &= A(-4)^2 + B(-4) + C \\[4pt] -4 &= A(1)^2 + B(1) + C \\[4pt] -2 &= A(3)^2 + B(3) + C \end{align}$$
These three equations can be solved simultaneously by methods you already know. We first use two sets of two equations to eliminate one of the variables (C is usually easiest in these problems), then use those two equations to solve for the other two, and finally use the results to find the third variable.
Here's how it looks. If we solve all three equations for C, we get:
$$ \begin{align} C &= 8 - 16A + 4B \\[4pt] C &= -4 - A - B \\[4pt] C &= -2 - 9A - 3B \end{align}$$
Now set two pairs of equations equal to one another, eliminating C: equations 1 and 2, 2 and 3:
$$ \begin{align} 8 - 16A + 4B &= -4 - A - B \\[4pt] -2 - 9A - 3B &= -4 - A - B \end{align}$$
and rearrange to:
$$ \begin{align} 15A - 5B &= 12 \\[4pt] 4A + B &= 1 \end{align}$$
Now we've reduced the problem to a two-equations, two-unknowns one. Let's multiply the lower equation by 5 to get
$$ \begin{align} 15A - 5B &= 12 \\[4pt] 20A + 5B &= 5 \end{align}$$
If we add those (remember that the left sides are equal to the right sides, so that has to be true for the sums, too), we get
$$35A = 17 \; \text{ or } \; A = \frac{17}{35}$$
Then it's easy to plug in $A$ to get $B = -33/35$ and $C = -124/35.$ So the equation of the parabola that fits through our three points is
$$f(x) = \frac{17}{35}x^2 - \frac{33}{35}x - \frac{124}{35}$$
which matches the graph above.
1. What it means to factor a quadratic equation of the form $x^2+Bx+C=0$
Minutes of your life: 2:42
3. Example of transforming between the vertex and standard forms of a quadratic function: $A(x-h)^2+k \; \leftrightarrow \; Ax^2+Bx+C$
Minutes of your life: 2:50
4. Completing the square: Example 1
In this example we complete the square to find the roots of a function for which we already know the roots. It's a good example to work through to see that completing the square works!
Minutes of your life: 2:46
5. Completing the square: Example 2
In this example, the quadratic function $f(x)=8x^2-20x-3$ has real roots, but it's not factorable. We complete the square to find the exact roots of the function. There is no difference between completing the square and using the quadratic formula, but I think that knowing how to complete the square will help you to understand a lot about basic algebra steps. You should learn it!
Minutes of your life: 2:58
7. Derivation of the quadratic formula – a must-see.
In this example, we start with $f(x)=Ax^2+Bx+C$ and complete the square to derive the quadratic formula.
Minutes of your life: 2:04 (and well worth it!)
8. Completing the square to obtain imaginary roots
In this example, we find the roots of $f(x) = 3x^2-4x+7$, which are imaginary (or more accurately, are complex with non-zero imaginary parts. We also use the discriminant to show how to determine before-hand that the roots of a quadratic function will be non-real.
Minutes of your life: 2:51

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.


