Graphs of trigonometric functions in this section use units of radians. If you're not familiar with or comfortable with radians, it's a simple conversion: π radians = 180˚. Look here for a refresher on angle measurement.
Waves are modeled by trigonometric functions
Waves are periodic disturbances in some medium, like water waves in water, vibrations of a string or wire (e.g. guitar), sound waves in air, or electromagnetic waves in the electromagnetic field. Those kinds of waves are covered in other sections. This section is about the mathematics we use to model wave behavior.
Pro tip:
Waves are not their medium. They are something that's happening to the medium. A water wave is not the water, just a periodic disturbance in the height of the water.
Waves are well-modeled using the fundamental trigonometric functions, sine and cosine.
In this section, we'll review the basic anatomy and transformations of a sine wave. It's the same for the cosine function; recall that the functions are the same except for a shift of π/2 along the time axis.
Anatomy of a wave
The graph below shows two cycles of a sine function. Time is along the horizontal axis, and $f(t)=\text{sin}(t)$ is plotted along the vertical axis. We need to become familiar with several terms that describe waves.
Peaks, troughs & amplitude
Waves have peaks or crests, the high points, and troughs, the low points. The amplitude of a wave is the measure of the height of a peak (or the depth of a trough) from the center line, or the line of zero displacement. The points at which the amplitude of a wave is zero are called nodes. If you've studied p-orbitals and d-orbitals in chemistry, you've learned about nodes of 3-dimensional waves.
Wavelength ($\lambda$)
Wavelength is the length, in units of length (e.g. meters), of one complete cycle or period of a wave. It's convenient to measure wavelength from node-to-node, peak-to-peak or trough-to-trough, but it can be anywhere, as long as the chunk of time represents one complete cycle of the wave. Wavelength is usually given the Greek symbol lambda, $\lambda$.
In later sections on this page, we'll develop other concepts such as frequency and phase of waves, then talk about the mathematical model of a wave.

Glossary of wave terms
| Term | Definition |
|---|---|
| Wave | A wave is a periodic disturbance in some medium like air, water, solid materials or the electromagnetic field. Waves have mathematically-predictable shapes. The wave is not the medium itself, but rather something that is happening to the medium. For example, a water wave isn't the water itself, but a motion of the water. |
| Medium | The medium is the "substance" through which the wave moves. Water waves move through water, sound waves can move through air, liquids or solids. Electromagnetic waves (light) can move through vacuum (absense of matter) which we call the electromagnetic field (once called the "ether." |
| Wavelength ($\lambda$) | The wavelength of a wave, denoted by the Greek letter lambda ( λ ), is the measure the length of one period or cycle of the repeated form. It is measured from one place on the wave to an identical place in the next cycle. We often cite wavelength as measured from "peak-to-peak" of the wave crests (tops). |
| Period (p) | The period of a wave is the time it takes for a complete wave to pass a point, or the time between wave crests. |
| Frequency ($\nu$) | The frequency of a wave, denoted by the Greek letter nu ( ν ), is the reciprocal of the period. Its units are "per second," or 1/s, which is called "Hertz" and has the symbol Hz. 1 Hz is also 1 cycle per second or cps. |
| Speed (s) | The speed of a wave is also called its speed of propagation. It's how fast the wave moves (or propagates) through some medium. The speed of sound in air is about 340 m/s. The speed of light in vacuum is $2.99792458 \times 10^8$ m/s (exactly), and it's a little slower in any other medium. |
| Amplitude (A) | The amplitude of a wave is its height, measured from the average (line of zero-displacement) to the top of a peak. It corresponds to the vertical scaling parameter, $A,$ from your knowledge of function transformations: $g(x) = \color{#E90F89}{A}f(x - h) + k.$ |
| Node | Nodes are points where a wave crosses the line of zero-displacement. The nodes of a water wave occur where the height of the wave is exactly equal to the level of the undisturbed water. Looking only at a node, an observer would not notice the wave. |
| Peak/trough | Peaks are high points of waves and troughs (trofs) are the low points. We often measure wavelength from one peak to the next. |
| Phase ($\phi$) | The phase of a wave is a relative concept. We can only speak of the phase of a wave relative to another. Phase is the right-left shifting of a wave along its axis of travel. It corresponds to the $h$ parameter in our list of function transformations: $g(x) = Af(x - \color{#E90F89}{h}) + k.$ Phase is always measured relative to the left-right position of another wave. Phase is unimportant in many situations, but in some, knowing relative phase is crucial. The waves produced by a laser are "coherent," meaning they're all "in phase." |
Wavelength and frequency
Imagine for a moment that your eyes are at the surface of the water of a smooth pool when a pebble is dropped in nearby. Waves will pass (say left to right) in time, and they'll pass at a speed that is limited by the medium — water in this case. From our experience, water waves move at about 1-2 meters per second.
Each medium has its own characteristic speed for waves passing through it. Sound waves travel at about 340 ms-1 in dry air, but they actually travel much faster through most solid materials, like steel or aluminum.
Light waves don't actually need a medium in which to travel. They are disturbances in the electromagnetic field, but more on that later. Light waves have the highest speed, $c = 2.99792458\times 10^8$ m/s (exactly).
Frequency
The number of waves that pass by a fixed point of view in some unit of time (usually a second) is called the frequency of the wave. Think of it as the measure of how frequently you'll see a wave crest. The units of frequency are "reciprocal seconds" ($s^{-1}$), and the reciprocal second is often called Hertz (Hz). A 240 Hz wave has a frequency of 240 per second (240 s-1= 240 Hz), and 240 waves pass a fixed point each second. (That would be some water wave).
The symbol for frequency is the Greek lower-case letter nu, $\nu$. It's basically a lower-case "v" that looks like the wind is blowing it over from the right.
Unit analysis
The unit of frequency is the reciprocal second,
Unit of $\nu$ is 1/s
and the unit of wavelength is a unit of length. We'll use the meter. So when we multiply frequency by wavelength, the units are the unit of speed:
$$\lambda \cdot \nu = m \left( \frac{1}{s} \right) = \frac{m}{s} = ms^{-1}$$
Thus, the product of wavelength and frequency is the speed of the wave.
$$\lambda \cdot \nu = \text{speed}$$
Here are some speeds of sound in various materials. Notice that the speed of sound in solid materials can be much larger than the speed of sound in air.

The unit of wavelength is the meter, and the unit of frequency is Hertz (Hz). $1 \; Hz = \frac{1}{s} = 1 \, s^{-1}.$
The wavelength ( λ ) of a wave multiplied by its frequency ( ν ) is its speed. In a given medium, an increase in wavelength means a decrease in frequency, and a decrease in wavelength means an increase in frequency.
$$\lambda \cdot \nu = \text{speed}$$
Example 1
The wavelength of the visible red beam of a helium-neon (HeNe) laser is 632.8 nm. Calculate the frequency of this light.
The wavelength-frequency equation for this kind of wave (electromagnetic radiation or light) is
$$\lambda \cdot \nu = 2.99 \times 10^8 \frac{m}{s}$$
where the speed of light is about 3 x 108 ms-1. Rearranging to solve for the frequency and plugging in the given wavelength (632 nm is red light), we get
$$\nu = \frac{2.99 \times 10^8 \, \frac{m}{s}}{632.8 \times 10^{-9} \, m}$$
The frequency is
$$\nu = 4.72 \times 10^{14} \; \text{Hz}$$
We should always try to simplify such numbers with our metric prefixes: 103 = Kilo (K); 106 = Mega (M), 109 = Giga (G), and 1012 = Tera (T). so this frequency is best presented in units of Terahertz (THz):
$$\nu = 472 \: \text{THz}$$
Example 2
The lower and upper ranges of human hearing are 20 Hz and 20,000 Hz (20 KHz). Calculate the wavelengths of these two sounds in dry air, in which the speed of sound is 340 ms-1
The wavelength-frequency equation is
$$\lambda \cdot \nu = 340 \, \frac{m}{s}$$
where the speed of sound (about 760 mi./h) is given. Rearranging to solve for the wavelength gives us:
$$\lambda = \frac{340 \, \frac{m}{s}}{\nu}$$
Now we can find the wavelength of the lower frequency (low-pitch sounds).
$$\lambda_1 = \frac{340 \, \frac{m}{s}}{\frac{20}{s}} = 17 \; m$$
and the higher frequency (high pitched sounds):
$$\lambda_2 = \frac{340 \frac{m}{s}}{\frac{20,000}{s}} = 0.017 \; m = 17 \; cm$$
So the waves most of us can hear have wavelengths between 17 cm and 17 m.
Amplitude
The sine function can be transformed in a number of different ways. The simplest is multiplication of the function by a constant, $A$, like this:
$$f(t) = A\cdot \text{sin}(t)$$
Here $A$ corresponds to the amplitude of the sine wave. So when using a sine function to model a wave, we can adjust the $A$ parameter to get the amplitude right.
The graph shows sine functions $f(t)=\text{sin}(t)$ and $g(t)=2\cdot\text{sin}(t)$, with amplitudes of 1 (blue) and 2 (gray), respectively.

Move the slider on the plot of $f(t) = A \, sin(t)$ below to see how changing the parameter A affects the graph.
For light waves, amplitude corresponds to brightness, and for sound waves it's volume (loudness).
Frequency
How do we increase or decrease the frequency of a sine wave to match the wave we're trying to model?
It turns out that changing the frequency is just stretching or compressing the function horizontally (along the time axis). It looks like this:
$$f(t) = \text{sin}(\omega t)$$
where $\omega$ is the Greek lower-case letter "omega," and is often called the frequency factor when the sine function is associated with waves.
The frequency factor is the number of full cycles of the sine wave that fit between $0$ and $2\pi$.
The graph shows two full cycles of $\text{sin}(t)$ (blue) between $0$ and $4\pi$, and four full cycles of $\text{sin}(2t)$ (gray) between $0$ and $4\pi$.

Move the slider below to change the frequency of this sine wave. Notice that as ω gets larger the number of cycles per unit time increases.
For light waves frequency corresponds to color. The electromagnetic spectrum spans radio waves at frequencies of just a few tens of Hz up through gamma rays with frequencies over 30 exahertz ($30 \times 10^{18}$ Hz). For sound waves, frequency corresponds to pitch. Human ears typically hear sounds between 20 Hz and 20,000 Hz (20 KHz).
Phase
The phase of a wave is unimportant in some applications, but crucial in others. You can think of a phase difference as the difference in relative "starting points" of two or more waves. Here's a picture. The magenta wave is shifted to the right by $\pi/2$ compared to the gray wave.

A phase shift of a sine wave is accomplished mathematically by employing the usual horizontal translation transformation:
$$f(t) = \text{sin}(t + \phi)$$
The Greek letter phi, $\phi$, is often used to denote phase.
Lasers produce what is called coherent light. This means that all waves have the sam phase, or are "in phase." In laser light all peaks and troughs line up and the range of emitted wavelengths is very tight. Compare that to a white light bulb, which produces light across the visible spectrum, and generally of all phases — non-coherent light.
Phase differences lead to all sorts of interesting and useful effects because they can produce constructive and destructive interference. More on that later.
Move the slider on the plot below to see how adjusting φ shifts the wave along the time (horizontal) axis.
Vertical offset
The last transformation of the sine function is the vertical translation or vertical shift. In wave mathematics it's sometimes called the vertical offset or DC offset (DC for "direct current").
The transformation is acheived by simply adding or subtracting a constant from the function,
$$f(t) = \text{sin}(t) + k$$
where $k$ is the offset. In the graph, a normal sine function is elevated by 2 units along the vertical axis by adding 2 to $f(x)$.

Move the slider on the plot of $f(t) = \text{sin}(t)$ below to see how the horizontal offset parameter ($k$) works.
Putting it all together – wave transformations
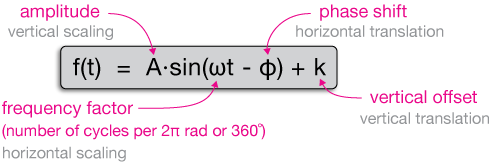
We can put all four wave transformations together into one equation. It's the wave equation you should know.
Interference
The periodic nature of waves allows them to add in interesting ways. Waves can interfere with each other, producing a wave of larger or smaller amplitude than its "parents." When waves add to increase the amplitude, we call it constructive interference. When they add to produce a lower amplitude than the absolute sum, it's destrucive interference. Perfect destructive interference between two waves can completely cancel both.
In this animation, two waves are added, point-by-point, along the t axis
Move the slider on the plot of
$$f(t) = \text{sin}(t) + \text{sin}(t - \phi)$$
below to see how changing the phase of one wave gradually diminishes the sum. When the waves are out of phase, that is their phases differ by π = 180˚, they cancel each other.
Finding a wave function from data
Now let's do a couple of examples of finding the functional form for a periodic phenomenon. The idea will be to take some phenomenon, such as tidal water depth or ... and determine the parameters, $A$ (amplitude), $\lambda$ (wavelength), $\phi$ (phase) and $k$ (vertical offset) from that data to form a complete function for the wave in the form of
$$f(t) = A \left( \frac{2 \pi}{\lambda} t + \phi \right) + k,$$
where $t$ is time.
Example 1
The data in the graph below are the tidal depths over 24 hours on Jan 27, 2021 (From Wolfram Alpha). Our goal will be to find a periodic function that models these data of the form
$$H(t) = A \left( \frac{2 \pi}{\lambda} t + \phi \right) + k,$$
where A is the amplitude, $\lambda$ is the wavelength, $\phi$ is the relative phase and k is the vertical offset. But first a little bit about tides.

Because of the Earth-moon physics, there are two high tides and two low tides each day. They are shown in the graph above. From left to right, they are the high low tide, the high high tide, the low low tide and the low high tide. Yes, those are their names, and they repeat like that every day.
Coos bay tides (1/27/2021) in feet from mean sea level
| Tide | Time | Level |
|---|---|---|
| High low | 03:56 | +4 feet |
| High high | 09:57 | +8.1 feet |
| Low low | 17:06 | -0.3 feet |
| Low high | 23:52 | +6.3 feet |
In first effort at modeling data, we'll ignore the differences between the two highs and the two lows and just think about making a model to predict the average high and low tide levels as a function of time.
The graph below has horizontal lines at the average of the high tides,
$$H = \frac{8.1 + 6.3}{2} = 7.2 \, \text{feet}$$
and at the average of the low tides:
$$L = \frac{4 - 0.3}{2} = 1.85 \, \text{feet}$$
So our wave will oscillate between heights of 1.85 and 7.2 ft. The amplitude is half of that distance, or
$$A = \frac{1}{2}(7.2 - 1.85) = 2.56 \, \text{feet}$$
The vertical offset from zero feet is just the average of those two levels,
$$k = \frac{7.2 + 1.85}{2} = 4.53 \, \text{feet}.$$
So far, our model looks like this:
$$H(t) = 2.56 \left( \frac{2 \pi}{\lambda} + \phi \right) + 4.53.$$

Now let's choose a sine wave for this model. Either sine or cosine is fine. Often one is as good as the other. We can estimate the wavelength of our wave at 12 hours, or ¼ of a day because there are two complete tide cycles (periods) every 24 hours.
Our model is thus improved to
$$H(t) = 2.56 \left( \frac{2 \pi}{12} + \phi \right) + 4.53.$$
The graph of this sine function has been superimposed in

Now what remains is to shift this wave left or right in order to get peaks and troughs to line up correctly. Let's go to the left (the choice is yours). If we look at the second peak of the model curve, it's currently about 10 hours too far to the right of the first peak of the data. To move it to the left would be to add a positive phase (which is just the horizontal translation we'd apply to any function) to the time variable inside the sine function, φ = 10
The resulting wave function is
$$H(t) = 2.56 \left( \frac{\pi}{6} + 10 \right) + 4.53.$$
(the $\frac{2 \pi}{12}$ fraction has been simplified.) This function is shown superimposed on the data in the graph below. It's not a bad model for the average of the high and low tides. It predicts the timing correctly, for sure.

How might we improve this model?
Notice that this model under-predicts the high-low and high-high tides and it over-predicts the low-low and low-high tides. How might we fix that? Well, that difference is also periodic, on a cycle of 24 hours.
It's possible to modify our function by adding a second sine wave that adds to the first two cycles of the current model and subtracts from the second two. I'll leave this as an exercise for you. A little thought, some calculations and a graphing calculator or program will get you there.
Video example
The Greek alphabet
| alpha | Α | α |
| beta | Β | β |
| gamma | Γ | γ |
| delta | Δ | δ |
| epsilon | Ε | ε |
| zeta | Ζ | ζ |
| eta | Η | η |
| theta | Θ | θ |
| iota | Ι | ι |
| kappa | Κ | κ |
| lambda | Λ | λ |
| mu | Μ | μ |
| nu | Ν | ν |
| xi | Ξ | ξ |
| omicron | Ο | ο |
| pi | Π | π |
| rho | Ρ | ρ |
| sigma | Σ | σ |
| tau | Τ | τ |
| upsilon | Υ | υ |
| phi | Φ | φ |
| chi | Χ | χ |
| psi | Ψ | ψ |
| omega | Ω | ω |
Parameter
A parameter is an adjustable constant in the definition of a function that is different from the independent variable(s). Parameters are not independent variables. For example, in the quadratic function
A, B and C are parameters which change the shape of the graph of the function. x is the independent variable. A, B and C are fixed for any particular version of f(x), but x can range from -∞ to +∞

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.