Taking derivatives to the next level
Implicit differentiation is a very powerful technique in differential calculus. It allows us to find derivatives when presented with equations like those in the box. →
One could solve for $y$ and find $y'(x)$ in the usual way, but there's an easier way, and it applies to the derivatives of more complicated curves, too.
Implicit differentiation is really just application of the chain rule, where we recognize that the $y$ variables in these equations are functions of the independent variable $x$, and further differentiate any term containing $y$ using the chain rule. For example,
$$\frac{d}{dx} \, y^n = n y^{n - 1} \frac{dy}{dx}$$
where $y = y(x).$
These equations all have graphs for which we might want to know the slope.
$$ \begin{align} x^2 + y^2 &= 4 \\[5pt] x^3 + y^3 &= 8 \\[5pt] (x - y)^2 &= x + y + 7 \\[5pt] \sqrt{x^2 + y^2} &= x \end{align}$$
Graphs of each of these relationships are shown below.
Example 1
If $x^2 + y^2 = 4$, find $\frac{dy}{dx}$
It's possible to solve for $y$ in this equation, of course, and then find $dy/dx$, but implicit differentiation makes finding the derivative much easier.
We start by taking the derivative with respect to $x$ (we could as easily take it with respect to $y$) of each term on both sides. We apply the sum rule (the derivative of a sum is the sum of derivatives) on the left and recall that the derivative of a constant is zero.
$$\frac{d}{dx} (x^2 + y^2) = \frac{d}{dx} 4$$
Here is an intermediate step:
$$\frac{d}{dx} x^2 + \frac{d}{dx} y^2 = 0$$
To differentiate $y^2$, we treat $y$ is a function of $x$ using the chain rule. Then it's a simple matter to solve for $\frac{dy}{dx}$.
$$2x + 2y \frac{dy}{dx} = 0$$
Moving the $2x$ to the right by subtraction and dividing by $2y$, gives us the solution:
$$\frac{dy}{dx} = \frac{-2x}{2y} = -\frac{x}{y}$$
Does the derivative make sense? The graph of this function is a circle centered at the origin, so we expect a positive slope in the 2nd and 4th quadrants, and a negative slope in the 1st and 3rd, just what we get from this derivative. Here's a picture of that:
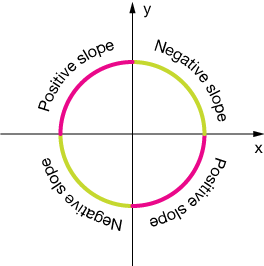
Implicit differentiation
When using implicit differentiation to find $\frac{dy}{dx},$ we differentiate terms with only the x-variable as usual, but for those containing y, we assume that y is some function of x, and use the chain rule. For example, $\frac{d(y^2)}{dx} = 2y \cdot \frac{dy}{dx}.$
Example 2
If $(x - y)^2 = x + y + 7,$ find $\frac{dy}{dx}$
To find $\frac{dy}{dx}$, we take the derivative of both sides with respect to $x$:
$$\frac{d}{dx} (x - y)^2 = \frac{d}{dx} (x + y + 7)$$
We need the chain rule on both the left and the right is just the derivative of a sum that will include $dy/dx$, remembering that $y$ is implicitly a function of $x$:
$$2(x - y)\left( 1 - \frac{dy}{dx} \right) = 1 + \frac{dy}{dx} + 0$$
Now we'll begin cleaning up and rearranging to solve for $\frac{dy}{dx}$:
$$(2x - 2y) \left( 1 - \frac{dy}{dx} \right) = 1 + \frac{dy}{dx}$$
Multiplying the two binomials on the left gives
$$2x - 2x\frac{dy}{dx} - 2y + 2y \frac{dy}{dx} = 1 + \frac{dy}{dx} $$
Now we'll collect all terms containing $dy/dx$ on the left, and factor out the $dy/dx$.
$$(2y - 2x - 1)\frac{dy}{dx} = 1 - 2x + 2y$$
Finally, it's just a matter of dividing by $2y - 2x - 1$ on both sides to find the derivative:
$$\frac{dy}{dx} = \frac{1 - 2x + 2y}{-1 - 2x + 2y}$$
Once again, we could isolate $y$ as a function of $x$ and just take a straightforward derivative, but solving for $y$ is not quite so easy. It would involve completing the square on $y$, then we'd be left with a tricky derivative. Implicit differentiation is much easier.
Here is a graph of curve represented by this equation, a tilted parabola.
Example 3
If $y = \text{sin}^{-1}(x)$, find $\frac{dy}{dx}$
Now we'll see how implicit differentiation can be a powerful tool for solving problems that we might not otherwise be able to, like finding the derivative of $y = \text{sin}^{-1}(x)$.
The first step is to take the sine of both sides, which 'cancels' the inverse sine on the right:
$$\text{sin}(y) = \text{sin}(\text{sin}^{-1}(x)) = x$$
Then take the derivative with respect to x of each side:
$$\frac{d}{dx} \text{sin}(y) = \frac{d}{dx} x$$
Now y is implicitly a function of $x$, so we have in instance of $dy/dx$:
$$\text{cos}(y) \frac{dy}{dx} = 1$$
Now it's just a matter of solving for $dy/dx$, as we've done before:
$$\frac{dy}{dx} = \frac{1}{\text{cos}(y)}$$
This solution isn't really what we want, however, because it's a function of $y$. To make it a function of $x$, we construct the triangle for which $sin(y) = x$.
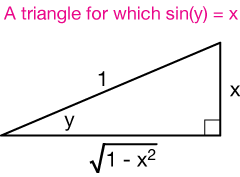
Now we can replace $cos(y)$ with the bottom side of the triangle in the figure:
$$\frac{dy}{dx} = \frac{1}{\sqrt{1 - x^2}}$$
We can derive a similar formula for the derivative of the inverse cosine function.
Example 4
Determine the equation of the line tangent to the graph of $y^4 + xy = 2x^3 - 7x - 7$ at the point $(1, 1)$.
First we will find $dy/dx$ by implicit differentiation, then plug $x = 1$ and $y = 1$ into it to find the slope at $(1, 1)$. Then the equation of the tangent is easy to find from the point and the slope.
The equation is
$$y^4 + xy = 2x^3 - 7x + 7$$
We need the slope, $dy/dx$, so we first differentiate the sums on each side of the equal sign, making sure to treat $y$ as an implicit function of $x$:
$$\frac{d}{dx} y^4 + \frac{d}{dx} xy = \frac{d}{dx}(2x^3 - 7x + 7)$$
We have to use the product rule to do the second derivative on the left, and the result is:
$$4y \frac{dy}{dx} + y + x\frac{dy}{dx} = 6x^2 - 7$$
Now if we gather terms in $dy/dx$ on the left, we get
$$(4y^3 + x) \frac{dy}{dx} = 6x^2 - 7x - y$$
Dividing by $4y^3 + x$ on both sides gives us our derivative, which we can evaluate at $(1, 1)$ to get the slope there:
$$\frac{dy}{dx} = \frac{6x^2 - 7 - y}{4y^3 + x} \bigg|_{(1, 1)} = \frac{-2}{5}$$
From there it's simple to use the slope and the point (1, 1) to find the equation of the tangent line. It's
$$2x + 5y = 7$$
Here's a graph of the equation and the tangent line. You can see that implicit differentiation allows us to do things with crazy, non-function equations that we might not have thought possible before.

Example 5
Find the locations of all vertical and horizontal tangents of the curve described by the curve $x + xy + 2x^3 = 2$
Our goal will be to find the derivative of the equation with respect to $x$, then find the zeros of its numerator (horizontal tangents) and the zeros of its denominator (vertical tangents). The function is
$$x + xy + 2x^3 = 2$$
If we take the implicit derivative, making sure to use the product rule on the second term ($xy$), we get:
$$1 + x \frac{dy}{dx} + y + 6x^2 = 0$$
Solving for dy/dx gives us the derivative, a function of x and y.
$$\frac{dy}{dx} = \frac{-6x^2 - y - 1}{x}$$
Sometimes that's not too convenient. In this case, we can, however, solve the original equation for $y$:
$$y = \frac{-2x^3 - x + 2}{x}$$
Dividing each term of the numerator by x gives us:
$y = -2x^3 - 1 + \frac{2}{x}$
We can take the derivative of $y(x)$ directly now to get
$$\frac{dy}{dx} = -4x - \frac{2}{x^2}$$
If we insert equation
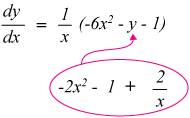
we get:
$$\frac{dy}{dx} = \frac{1}{x}(-6x^2 + 2x^2 + 1 - \frac{2}{x} - 1)$$
which simplifies to this:
$$\frac{dy}{dx} = \frac{1}{x \left( -4x^2 - \frac{2}{x} \right)}$$
and finally dividing by $x$ gives us the same derivative:
$$\frac{dy}{dx} = -4x - \frac{2}{x^2}$$
Now finding the horizontal tangent(s) means setting that derivative equal to zero:
$$-4x - \frac{2}{x^2} = 0$$
Moving one term to the other side gives us:
$$-4x = \frac{2}{x^2}$$
Multiplying both sides by $x^2$ and simplifying the constant gives us a cubic equaiton that can be solved
$$x^3 = -\frac{1}{2}$$
The result is the location of a single horizontal tangent at
$$ \begin{align} x &= -0.794 \\[5pt] y &= 2.779 \end{align}$$
Vertical tangent(s) occur when the denominator of the derivative is zero. Taking the implicit derivative, we see that it goes to zero when $x$ goes to zero:
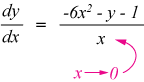
Here is a graph of the function showing the single horizontal tangent and the vertical tangent, at which the function has no value.

Practice problems
Find the derivative of each with respect to x.
-
$3 y^3 + x^2 = 5$
Solution
$$ \begin{align} 3 y^3 + x^2 &= 5 \\[5pt] \frac{d}{dx} \left( 3y^3 + x^2 \right) &= \frac{d}{dx}5 \\[5pt] 9y^2 \frac{dy}{dx} + 2x &= 0 \\[5pt] \frac{dy}{dx} &= \frac{-2x}{9y^2} \end{align}$$
-
$y^4 - 2y = 4x^3 + x$
Solution
$$ \begin{align} y^4 - 2y &= 4x^3 + x \\[5pt] \frac{d}{dx}(y^4 - 2y) &= \frac{d}{dx}(4x^3 + x) \\[5pt] 4y^3\frac{dy}{dx} = 2\frac{dy}{dx} &= 12x^2 + 1 \\[5pt] \frac{dy}{dx}(4y^3 - 2) &= 12x^2 + 1 \\[5pt] \frac{dy}{dx} &= \frac{12x^2 + 1}{4y^3 - 2} \end{align}$$
-
$x^2y + 2x^3 y = x + y$
Solution
$$ \begin{align} x^2y + 2x^3y &= x + y \\[5pt] \frac{d}{dx}(x^2y + 2x^3y) &= \frac{d}{dx}(x + y) \\[5pt] 2xy + x^2\frac{dy}{dx} + 6x^2y + 2x^3\frac{dy}{dx} &= 1 + \frac{dy}{dx} \\[5pt] \frac{dy}{dx}(x^2 + 2x^3 - 1) &= 1 - 2xy - 6x^2y \\[5pt] \frac{dy}{dx} &= \frac{1 - 2xy - 6x^2y}{x^2 + 2x^3 - 1} \end{align}$$
-
$xy^2 + x^2y^5 - x^3 = 3$
Solution
$$ \begin{align} xy^2 + x^2y^5 - x^3 &= 3 \\[5pt] \frac{d}{dx}(xy^2 + x^2y^5 - x^3) &= \frac{d}{dx}3 \\[5pt] y^2 + 2xy \frac{dy}{dx} + 2xy^5 + 5x^2y^4 \frac{dy}{dx} - 3x^2 &= 0 \\[5pt] \frac{dy}{dx}(2xy + 5x^2y^4) &= 3x^2 - 2xy^5 - y^2 \\[5pt] \frac{dy}{dx} &= \frac{3x^2 - 2xy^5 - y^2}{2xy + 5x^2y^4} \end{align}$$
-
$x^3 y^5 = 1$
Solution
$$ \begin{align} x^3y^5 &= 1 \\[5pt] \frac{d}{dx}(x^3y^5) &= \frac{d}{dx} 1 \\[5pt] 3x^2y^5 + 5x^3y^4\frac{dy}{dx} &= 0 \\[5pt] \frac{dy}{dx}(5x^3y^4) &= -3x^2y^5 \\[5pt] \frac{dy}{dx} &= \frac{-3x^2y^5}{5x^3y^4} \end{align}$$
-
$x^4 + y^4 = 1$
Solution
$$ \begin{align} x^4 + y^4 &= 1 \\[5pt] \frac{d}{dx}(x^4 + y^4) &= \frac{d}{dx} 1 \\[5pt] 4x^3 + 4y^3\frac{dy}{dx} &= 0 \\[5pt] 4y^3 \frac{dy}{dx} &= -4x^3 \\[5pt] \frac{dy}{dx} &= \frac{-x^3}{y^3} \end{align}$$
-
$\frac{y}{x} + \frac{x}{y} = 2y$
Solution
$$ \begin{align} \frac{y}{x} + \frac{x}{y} &= 2y \\[5pt] \frac{d}{dx}\left(\frac{y}{x} + \frac{x}{y}\right) &= \frac{d}{dx} (2y) \\[5pt] \frac{x\frac{dy}{dx} - y}{x^2} + \frac{y - x\frac{dy}{dx}}{y^2}&= 2\frac{dy}{dx} \\[5pt] \frac{xy^2\frac{dy}{dx} - y^3 + x^2y - x^3\frac{dy}{dx}}{x^2y^2} &= 2\frac{dy}{dx} \\[5pt] \frac{dy}{dx}(xy^2 - x^3) &= 2x^2y^2 \frac{dy}{dx} + y^3 - x^2y \\[5pt] \frac{dy}{dx}(xy^2 - x^3 - 2x^2y^2) &= y^3 - x^2y \\[5pt] \frac{dy}{dx} = \frac{y^3 - x^2y}{xy^2 - x^3 - 2x^2y^2} \end{align}$$
-
$\sqrt{x + y} = \frac{1}{x} + \frac{1}{y}$
Solution
$$ \begin{align} \sqrt{x + y} &= \frac{1}{x} + \frac{1}{y} \\[5pt] \frac{d}{dx}(\sqrt{x + y}) &= \frac{d}{dx}\left( \frac{1}{x} + \frac{1}{y} \right) \\[5pt] \frac{1}{2}(x + y)^{-1/2}\left( 1+ \frac{dy}{dx} \right) &= -x^{-2} - y^{-2} \frac{dy}{dx}\\[5pt] \frac{dy}{dx}\left( \frac{1}{2\sqrt{x + y}} + \frac{1}{y^2} \right) &= \frac{-1}{2 \sqrt{x + y}} - \frac{1}{x^2} \\[5pt] \frac{dy}{dx}\left( \frac{y^2 + 2\sqrt{x + y}}{2 y^2 \sqrt{x + y}} \right) &= \frac{-x^2 - 2\sqrt{x + y}}{2x^2\sqrt{x + y}} \\[5pt] \frac{dy}{dx} &= \frac{2y^2 \sqrt{x + y}}{y^2 + 2\sqrt{x + y}} \cdot \frac{-x^2 - 2\sqrt{x + y}}{2x^2\sqrt{x + y}} \\[5pt] \frac{dy}{dx} &= \frac{y^2 (-x^2 - 2\sqrt{x + y})}{x^2 (y + 2\sqrt{x + y})} \end{align}$$
-
$y^{-2/3} + x^{3/2} = 1$
Solution
$$ \begin{align} y^{-2/3} + x^{3/2} &= 1 \\[5pt] \frac{d}{dx}\left( y^{-2/3} + x^{3/2} \right) &= \frac{d}{dx} 1 \\[5pt] -\frac{2}{3} y^{-5/3}\frac{dy}{dx} + \frac{3}{2}x^{1/2} &= 0 \\[5pt] \frac{dy}{dx} &= \frac{3x^{1/2}}{2} \cdot \frac{3 y^{5/3}}{2} \\[5pt] &= \frac{9}{4}x^{1/2} y^{5/3} \end{align}$$
-
$x^{3/2} + y^{1/3} = -5y$
Solution
$$ \begin{align} x^{3/2} + y^{1/3} &= -5y \\[5pt] \frac{d}{dx}\left( x^{3/2} + y^{1/3} \right) &= \frac{d}{dx} (-5y) \\[5pt] \frac{3}{2} x^{1/2} + \frac{1}{3}y^{-2/3}\frac{dy}{dx} &= -5\frac{dy}{dx} \\[5pt] \frac{dy}{dx}\left( \frac{1}{3y^{2/3}} + 5 \right) &= -\frac{3}{2}x^{1/2} \\[5pt] \frac{dy}{dx} &= \frac{-3x^{1/2}}{2} \cdot \frac{1 + 15y^{2/3}}{3y^{2/3}} \end{align}$$
-
$y + \frac{1}{y} = x^3 + x$
Solution
$$ \begin{align} y + \frac{1}{y} &= x^3 + x \\[5pt] \frac{d}{dx}\left( y + \frac{1}{y} \right) &= \frac{d}{dx} (x^3 + x) \\[5pt] \frac{dy}{dx} - \frac{1}{y^2}\frac{dy}{dx} &= 3x^2 + 1 \\[5pt] \frac{dy}{dx}\left( \frac{y^3 - 1}{y^2} \right) &= 3x^2 + 1 \\[5pt] \frac{dy}{dx} &= \frac{(3x^2 + 1)y^2}{y^3 - 1} \end{align}$$
-
$\text{sin}(xy) = x$
Solution
$$ \begin{align} \text{sin}(xy) &= x \\[5pt] \frac{d}{dx} \text{sin}(xy) &= \frac{d}{dx} x \\[5pt] \\text{cos}(xy)\left[ y + x \frac{dy}{dx} \right] &= 1 \\[5pt] y \text{cos}(xy) + x \text{cos}(xy)\frac{dy}{dx} &= 1 \\[5pt] \frac{dy}{dx} &= \frac{1 - y \text{cos}(xy)}{x \text{cos}(xy)} \end{align}$$
-
$\text{sin}(x + y) = x + \text{cos}(y)$
Solution
$$ \begin{align} \text{sin}(x + y) &= x + \text{cos}(y) \\[5pt] \frac{d}{dx} \text{sin}(x + y) &= \frac{d}{dx} (x + \text{cos}(y)) \\[5pt] \text{cos}(x + y)\left[ 1 + \frac{dy}{dx} \right] &= 1 - \text{sin}(y)\frac{dy}{dx} \\[5pt] \frac{dy}{dx}\left[ \text{cos}(x + y) + \text{sin}(y) \right] &= 1 - \text{cos}(x + y)\\[5pt] \frac{dy}{dx} &= \frac{1 - \text{cos}(x + y)}{\text{cos}(x + y) + \text{sin}(y)} \end{align}$$
-
$\text{tan}(x^2 y) = (x + y)^2$
Solution
$$ \begin{align} \text{tan}(x^2 y) &= (x + y)^2 \\[5pt] \frac{d}{dx} \text{tan}(x^2 y) &= \frac{d}{dx} [(x + y)^2] \\[5pt] \text{sec}^2(x^2 )\left[2xy + x^2 \frac{dy}{dx} \right] &= 2(x + y)\left(1 + \frac{dy}{dx}\right) \\[5pt] 2xy \, \text{sec}^2(x^2y) + \frac{dy}{dx}[x^2 \text{sec}^2(x^2y)] &= 2x + 2x\frac{dy}{dx} + y + y\frac{dy}{dx} \\[5pt] \frac{dy}{dx}[x^2 \text{sec}^2(x^2y) - 2x - y] &= 2x + y - 2xy \,\text{sec}^2(x^2y)\\[5pt] \frac{dy}{dx} &= \frac{2x + y - 2xy \,\text{sec}^2(x^2y)}{x^2 \text{sec}^2(x^2y) - 2x - y} \end{align}$$
Implicit differentiation can be the best route to what otherwise could be a tricky differentiation. In example 3 above we found the derivative of the inverse sine function. We can use that as a general method for finding the derivative of any inverse function.
Recall that if $f(x)$ is a function and $f^{-1}(x)$ is its inverse, that
$$f(f^{-1}(x)) = f^{-1}((f(x)) = x$$
In other words, a function and its inverse "undo" one another.
To find the derivative of an inverse function, begin with
$$f(f^{-1}(x)) = x$$
Now differentiate both sides with respect to x, but be aware that the left side is a composition of functions, and will require the chain rule:
$$\frac{d}{dx} \, f(f^{-1}(x)) = \frac{d}{dx} \, x$$
The chain rule gives us:
$$f'(f^{-1}(x)) \cdot f'^{-1}(x) = 1$$
where $f^{-1}(x)$ is the derivative of the inverse. Solving for the derivative of the inverse, we get:
$$\frac{d}{dx} f^{-1} (x) = \frac{1}{f'(f^{-1}(x))}$$
So to find the derivative of the inverse of the function at a point $x$, we substitute the inverse function for $x$ in $f'(x)$, then take the reciprocal.
Derivative of the inverse of a function
The derivative of the inverse of a function is equal to the reciprocal of the compound function $f'(f^{-1}(x))$. We need to know the inverse function and the derivative of its inverse.
$$\frac{d}{dx} f^{-1}(x) = \frac{1}{f'(f^{-1}(x))}$$

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.