Gravity: One of the four fundamental forces
Gravity is a non-contact force (a force that can be exerted on a body without touching it), one of four fundamental non-contact forces we know of. They are
the gravitational force (gravity)
the electromagnetic force (the force between charged particles or poles of magnets)
the weak nuclear force
the strong nuclear force
The latter two are active only at distances as small as those present between protons and neutrons in the nuclei of atoms. Sometimes a non-contact force is called "force at a distance."
Unlike the other three forces, gravity is a purely attractive force. If we bring a negative and a positive charge together, the electrostatic force is attractive (brings them together). But if we bring two positive charges or two negative charges together, they repel one another (opposites attract, likes repel). There is no such repulsive component to the gravitational force; you never see someone walking down the street suddenly get ejected from the planet by gravity.
Isaac Newton and others determined, mostly from astronomical data — observations of the motions of planets in the sky — that the gravitational attraction is a property of mass, that it is proportional to the product of the two masses involved, and that it is inversely proportional to the square of the distance between their centers of mass. Here is the definition:

This diagram shows the picture that the law of gravitation describes:

The Universal Law of Gravitation
The Universal Law of Gravitation says that the force, $F_g$, between two objects of mass $m_1$ and $m_2$ is directly proportional to the product of the masses and inversely proportional to the square of the distance, $r$, between them. The proportionality constant (which just gets the units right) is $G = 6.674 \times 10^{-11} \, N\cdot m^2 Kg^{-2}$.
$$F_g = \frac{G m_1 m_2}{r^2}$$
Reminder about negative exponents
A negative exponent means "take the reciprocal." You'll see negative exponents in units a lot because it's easier to type on one line. Get to know what they mean and how to use them. Also see the page on rational and negative exponents.
| Negative exponents | Fraction |
|---|---|
| $$Kg \cdot m \cdot s^{-2}$$ | $$\frac{Kg \cdot m}{s^2}$$ |
| $$N \cdot m^2$$ | $$\frac{N}{m^2}$$ |
| $$N \cdot m^2 \cdot Kg^{-2}$$ | $$\frac{N \cdot m^2}{Kg^2}$$ |
The gravitational constant, $G$, is a fundamental constant of the universe. You can think of such constants as fixed numbers that are there for us to get the units correct. When we multiply two masses and divide by a length squared, we need to end up with units of force ($1N = 1 \, Kg\cdot m/s^2$). If we used different units, $G$ would be different. What's important is the proportionality of the masses and the distance to the gravitational force.
You should also know how to rearrange the Universal Law of Gravity to solve for either force, mass or distance, $r \rightarrow$

Units of force
The unit of force is the Newton ($N$), $1 \, N = 1 \, Kg\cdot m \cdot s^2$. The Newton is the units of acceleration ($m \cdot s^{-2}$) multiplied by mass.
$$1 \; N \; = \; \frac{1 \; Kg \, m}{s^2} \; = \; 1 \; Kg \, m \, s^{-2}$$
You should memorize the underlying units of the Newton. They'll come in handy later.
Dependence of gravitational force on mass and distance
The graph below shows how the force of gravity ($F_g$) varies as one of the masses is increased from zero and the other is held constant. $F_g$ is directly and linearly proportional to each mass — thus the linear graph.
Effect of changing one mass

We generally think of gravity in terms of one variable mass and one fixed mass, like a planet. The force of gravity is greater on a more massive person than a less massive person, therefore the more massive person weighs more — weight, unlike mass, is a measure of force.
The gravitational force on the moon is 1/6 that on Earth because the mass of the moon is about 1/6 the mass of Earth.
The universal law of gravitation is called an inverse-square law because the force is inversely proportional to the square of the distance between two masses.
We will see another inverse square law when we study the electrostatic force.
The important thing about this feature of gravity is that if we double the distance between objects, the force of gravity is reduced by a factor of four ($2^2$), not two. The graph shows that when r, the distance between masses, is small, the gravitational force is high, but as r is increased, the force drops non-linearly. The graph of force vs. the separation distance is quadratic:
Effect of changing distance ($r$)

Orbits
A question that plagued early astronomers was: "What makes a moon orbit a planet?" or "What makes a planet orbit the sun?" It turns out that is kind of the wrong question, but it's not too bad for starting place, so for now, let's say the Moon revolves around Earth (they actually both orbit a common center of mass, but more on that later ...)

Richard Feynman points out that some early astronomers attributed the motion of the moon and planets to "invisible angels" who push from behind. This idea underscores the notion that for a long time observers were stuck on the idea that there must be some force pushing in the direction of the motion. That makes sense, of course: If there's a baby carriage moving down the street, we pretty much expect the force to be applied from behind, not from the side.
But the fact is that no such force is required for orbital motion. The only force needed to keep a planet in its orbit is gravitational attraction, a center-seeking or centripetal force.
Orbits: balance between gravity and inertia
Orbiting is a perfect balance between inertia, the tendency of a body to move in a straight line (not a curve) until acted upon by a force, and the attractive force of gravity.
As the Moon orbits Earth, it has inertia, which always moves it in a direction tangential to the orbital path (nearly a circle). But for every bit of tangential motion, there is some inward motion that keeps the path bent exactly to the orbital path.
The notes on acceleration might help you understand this idea, too.
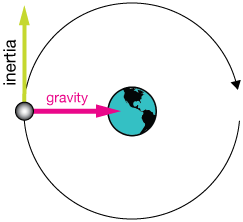
Only a centripetal (center-seeking) force, like gravity, is required to keep bodies in orbit around one another.
Achieving orbit
Here's another way to think about orbiting: Imagine you've got quite an arm (QUITE an arm), and can throw a baseball very fast. How fast would you need to throw it so that as it travels, the bending away of the spherical Earth below it is just balanced by the downward distance it is pulled by gravity — it orbits just above the surface?

Look at the scenario above. If you throw the ball parallel to the surface (Earth is big – it seems flat to us) at a velocity that produces some forward distance in a given time (let's say a second) that does not keep up with the downward distance caused by the pull of gravity, the ball will eventuall land.
4.9 m/s would be fine for one meter, but even though the Earth curves away below the path of the ball, Earth is large, and the next second (because the ball is accelerating) carries the ball 14.7 meters down -- smack.
Now imagine that you throw the ball with sufficient speed that the curvature of Earth gives it enough extra height in any given period of time that the amount of distance it falls due to gravity is just enough to keep it a fixed distance away from the ground. (We're assuming that Earth is a perfectl sphere here, and that there's no air resistance).
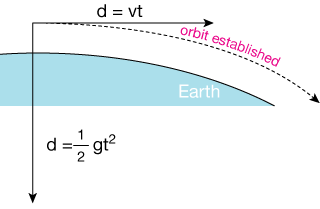
That's what it means to orbit. The forward inertia of the ball keeps it moving forward and gravity bends that path into a curve (an ellipse, actually, but remember that a circle is just a special kind of ellipse).
So how fast do you need to throw the ball in order to achieve orbit? Let's sketch a picture of Earth with some dimensions. In the first second, the ball will travel 4.9 meters toward the center of Earth:

The radius of Earth is about $r = 4 \times 10^6 \,m$, so
$$d^2 = (r + 4.9)^2 - r^2$$
The ball needs to travel d = 6261 m in order to remain just above the surface of Earth. In one second, that's about 14,000 mi./h or 3.9 mi./s
That's really quite a speed, and it partly explains why it's so difficult to get objects to orbit Earth. Generally when we fire off a satellite, the rocket that carries it accelerates straight upward until it clears most of the friction-producing atmosphere, then turns over to accelerate to a tangential velocity that is fast enough to achieve a stable orbit. Higher satellites don't need to orbit as fast.
Geosynchronous satellites travel at a tangential velocity of about 7,000 miles/hour, just matching the rotational speed of the surface of Earth (you are moving at about 1000 mi./h right now!), thus they are always in the same place in the sky.
Planets actually orbit each other
Now to refine our picture of orbiting a bit. Remember that ever body in the universe exerts a mass-proportional amount of gravity on every other body. Thus while Earth exerts a force on the Moon that keeps it in orbit, the Moon also exerts a force on Earth. It's why we have tides.
Orbiting objects actually orbit each other, each moving about a common center of mass. The location of the center of mass of the Earth-Moon system (the point where the two, if joined by a stick, would balance) is somewhere inside of Earth because Earth is about 6 times more massive than the moon. Think of a seesaw: Where does the light person need to be in order to balance the weight of a heavy person?
This animation shows how simple orbits work. The dashed circle stays where it was at the beginning to help you see the circular motion of the larger planet. The red dot is the center of mass.
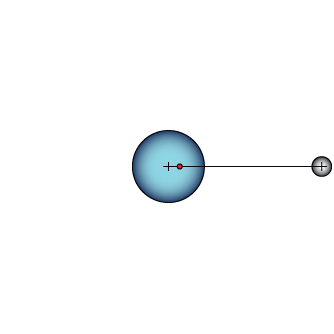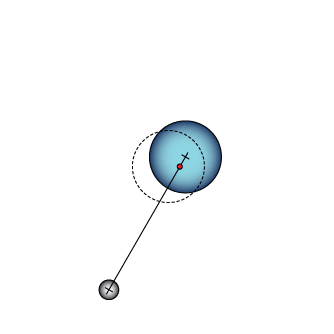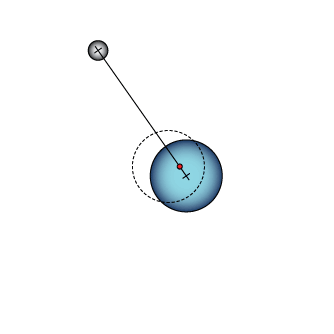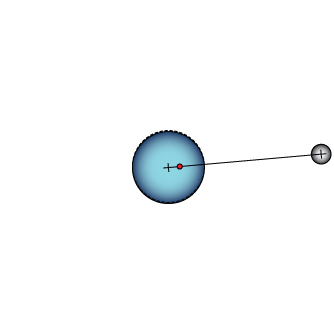
Perspective on orbits
Most artificial Earth satellites orbit at between 160 and 2000 Km. The radius of Earth is about 6400 Km, so these are considered to be near-Earth orbits (NEO). The force of gravity on these satellites isn't that much smaller than on Earth, but they are actually in free-fall. At these altitudes it takes satellites between 90 min. and 2 hours to complete one orbit. The international space station has a 90-93 minute orbit at about 410 Km.

Practice problems
-
Calculate the force of attraction between a 3 Kg baby and the physician who delivers it. Assume the physician has a mass of 100 Kg and is 0.5 m from the baby. Then calculate the force of gravity between Mars and the same baby. The mass of Mars is about 6.4 × 1023 Kg and is closest to Earth when it is about 5.6 × 1010 meters away. Which exerts more gravitational force on the baby, the doctor or Mars?
Solution
$$F = \frac{G m_p m_b}{r^2}$$
where mp is the mass of the physician, mb is the mass of the baby, and r is the distance between the baby and the physician.
$$ \begin{align} F &= \frac{\left(6.674 \times 10^{-11} \frac{m^3}{Kg s^2}\right)\left( 100 \, Kg \right)(3 \, Kg)}{0.5^2 \, m^2} \\[5pt] &= 8.0 \times 10^{-8} \, N \end{align}$$
Compare this force with that calculated in problem 1. The physician exerts twice the force on the child as Mars, so the next time someone tells you that where Mars is in its orbit will affect your life, you can reply that having a thin or thick doctor might make even more difference.
-
Calculate the weight, in Newtons and in pounds, of the Mars curiosity rover, which has a mass of 899 Kg, on both Earth and Mars. (Mass of Earth = 5.972 x 1024 Kg; mass of Mars = 6.4 x 1023 Kg; radius of Earth = 6.371 x 106 m; radius of Mars = 3.397 x 106 m)
Solution
$$ \begin{align} F &= \frac{G m_1 m_2}{r^2} \\ F &= \frac{\left(6.674 \times 10^{-11} \frac{m^3}{Kg s^2}\right)(5.972 \times 10^{24} \, Kg)(899 \, Kg)}{(6.371 \times 10^6 \, m)^2} \\[5pt] &= 8,827 \, N = 1,984 \; lbs. \end{align}$$
Mars
$$ \begin{align} F &= \frac{G m_1 m_2}{r^2} \\ F &= \frac{\left(6.674 \times 10^{-11} \frac{m^3}{Kg s^2}\right)(6.4 \times 10^{23} \, Kg)(899 \, Kg)}{(3.397 \times 10^6 \, m)^2} \\[5pt] &= 3,328 \, N = 748 \; lbs. \end{align}$$
There's much less force on the rover on Mars than on Earth. That might figure into the engineering of suspension, expected wear and tear, &c.
-
How far apart (in meters) must two 1000 Kg spherical masses be in order to exert a 0.01 N force on each other?
Solution
First, rearrange the universal law of gravity to solve for the distance, r.
$$F = \frac{G m_1 m_2}{r^2} \; \longrightarrow \; r = \left( \frac{G m_1 m_2}{F} \right)^{1/2}$$
$$ \begin{align} r &= \left( \frac{6.674 \times 10^{-11} \frac{m^3}{Kg s^2}\cdot 1000 \, Kg \cdot 1000 \, Kg}{0.01 \frac{Kg m}{s^2}} \right)^{1/2} \\[5pt] &= 0.082 \; m = 8.2 \; cm \end{align}$$
-
The mass of the moon is 7.34767309 × 1022 Kg, and its radius is 1737.4 Km. Calculate the acceleration of gravity on the moon. (See the calculation of g below for an example.)
Solution
$$F = \frac{G m_m m}{r_m^2}$$
where mm is the mass of the moon, and m is the mass of whatever object we'll be considering; r is the radius of the moon.
$$F = g\cdot m, \; \text{ where}$$
$$ \begin{align} g &= \frac{G m_m}{r_m^2} \\ &= \frac{6.674 \times 10^{-11} \frac{m^3}{Kg s^2} \cdot 7.3476 \times 10^{22} \, Kg}{1.7374 \times 10^6 \; m)^2} \\[5pt] &= 1.624 \, \frac{m}{s^2} \end{align}$$
This is about 1/6 the acceleration of gravity on Earth.
Finding g
Acceleration of gravity near the surface of Earth
We can use the universal law of gravitation to find the acceleration of gravity near the surface of Earth (below). Let one of the masses be the mass of Earth, mE and rE = the radius of Earth.
The universal law of gravitation is then:
$$F = \frac{G \, m_E \cdot m}{r_E^2},$$
where mE is the mass of Earth and rE is the radius of Earth. Now notice that this equation bears a resemblance to Newton's second law, F = ma, where a is the acceleration, which in this case would be the acceleration due to gravity, g. So we have:
$$F = \color{#E90F89}{\frac{G \, m_E}{r_E^2}} m,$$
where the
Now we can plug in the mass and radius of Earth to get g:
← scroll →
$$ \require{cancel} \begin{align} \frac{G m_E}{r^2} &= \frac{6.67398 \times 10^{-11} \frac{m^3}{\cancel{Kg} s^2} 5.97219 \times 10^{24} \cancel{Kg}}{(6.371 \times 10^5 m)^2} \\[5pt] &= \frac{6.67398 \times 10^{-11} \frac{m^{\cancel{3}}}{s^2} 5.97219 \times 10^{24}}{4.059 \times 10^{13} \cancel{m^2}} \\[5pt] &= 9.819 \, \frac{m}{s^2} \end{align}$$
g = 9.81 m/s2 is just what we expect. Note that this is not how g was calculated historically. It's much easier to measure g using balls and ramps, or other apparatus, and calculate the mass of Earth from it and the universal law of gravitation – sort of like we did here. Still, this is a useful exercise in manipulating these equations.
Variation of g across the globe

Video examples
Example 1
Use the universal law of gravity to calculate the gravitational force between Earth and its only moon.
Minutes of your life: 3:00
Example 2
Calculate the change in gravitational force when one body is moved away from another.
Minutes of your life: 3:09
Example 3
Using Newton's second law, F = m·a, calculate the acceleration of gravity near the surface of Earth's moon.
Minutes of your life: 3:06
Example 4
Use the universal law of gravity to calculate the gravitational force between a proton and an electron in a hydrogen atom. (it's very small!)
Minutes of your life: 2:48
The Lagrange point (optional)
The point where the gravitational forces between two bodies balance
The Lagrange point is the place on a line between two objects (usually planets or stars) where the gravitational pull of one body matches the pull of the other, and there is no net gravitational force on an object in between. Let's illustrate this idea by finding the Lagrange point between Earth and its moon. We expect it, of course, to be closer to the moon because the mass of Earth is so much greater.
We'll do this algebraically most of the way before we plug in numbers. That way we'll end up with a formula we can apply to other systems.
It begins with setting up the gravitational force between Earth and some object of mass m, and the equivalent force due to the moon. Here's the geometry:

The forces are
$$F_E = \frac{G m \, m_E}{x^2} \phantom{000} F_M = \frac{G m \, m_M}{(d - x)^2},$$
where d is the mean distance between Earth and the moon. Now we want those two forces to be equal, so we'll set the expressions to be equal to each other, noting that we can immediately cancel G and m, our "test mass."
$$ \require{cancel} \begin{align} \frac{\cancel{G m} m_E}{x^2} &= \frac{\cancel{G m} m_E}{(d-x)^2} \\[5pt] \frac{m_E}{x^2} &= \frac{m_M}{(d - x)^2} \end{align}$$
Now we want to solve for x, so we'll cross multiply, expand the squared binomial and collect terms to make a nice (even if it doesn't look nice) quadratic equation:
$$ \begin{align} m_E (d - x)^2 &= m_M x^2 \\[5pt] m_E (x^2 - 2dx + d^2) &= m_M x^2 \\[5pt] (m_E - m_M)x^2 - 2dm_E x + d^2 m_E &= 0 \end{align}$$
Now let's solve for x by completing the square. I'll go through all of the steps here without annotating them, but you can use the link above to refresh your memory if you've forgotten.*
*
← wide equations: scroll left/right →
$$ \begin{align} x^2 - \frac{2dm_E \, x}{m_E - m_M} + \frac{d^2 m_E}{m_E - m_M} &= 0 \\[5pt] x^2 - \frac{2dm_E \, x}{m_E - m_M} &= -\frac{d^2 m_E}{m_E - m_M} \\[5pt] x^2 - \frac{2dm_E \, x}{m_E - m_M} + \left(\frac{d m_E}{m_E - m_M}\right)^2 &= \frac{d^2 m_E^2}{(m_E - m_M)^2} - \frac{d^2 m_E}{m_E - m_M} \\[5pt] \left( x - \frac{d m_E}{m_E - m_M} \right)^2 &= \frac{d^2 m_E^2 - d^2 m_E (m_E - m_M)}{(m_E - m_M)^2} \\[5pt] \left( x - \frac{d m_E}{m_E - m_M} \right)^2 &= \frac{\cancel{d^2 m_E^2} - \cancel{d^2 m_E^2} + d^2 m_E m_M}{(m_E - m_M)^2} \\[5pt] \left( x - \frac{d m_E}{m_E - m_M} \right)^2 &= \frac{d^2 m_E m_M}{(m_E - m_M)^2} \\[5pt] x &= \frac{d m_E}{m_E - m_M} ± \sqrt{\frac{d^2 m_E m_M}{(m_E - m_M)^2}} \\[5pt] x &= \frac{d\left(m_E ± \sqrt{m_E m_M}\right)}{m_E - m_M} \\[5pt] \end{align}$$
Now the plus solution turns out to be greater than d in all cases, so we'll throw that out (there is actually another Lagrange point on the far side of the moon, but we'll just focus on the one in between). Our Lagrange point is the minus solution:
$$x = \frac{d\left(m_E - \sqrt{m_E m_M}\right)}{m_E - m_M}$$
Now we can plug in our masses and the distance d,
$$ \begin{align} m_E &= 5.9742 \times 10^{24} \, Kg \\[5pt] m_M &= 7.36 \times 10^{22} \, Kg \\[5pt] d &= 3.844 \times 10^8 \, m, \end{align}$$
which gives us
← scroll →
$$ \begin{align} 3.844 &\times 10^8 \left( \frac{5.9742 \times 10^{24} - \sqrt{5.9742 \times 10^{24} - 7.36 \times 10^{22}}}{5.9742 \times 10^{24} - 7.36 \times 10^{22}} \right) \\[5pt] &= (3.844 \times 10^8 \, m)(0.9) \end{align}$$
So the Lagrange point between Earth and the moon is about 90% of the way to the moon.

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.