Derivatives of the trigonometric functions
In this section we'll derive the important derivatives of the trigonometric functions $f(x) = \text{sin}(x)$, $\text{cos}(x)$ and $\text{tan}(x)$.
In doing so, we will need to rely upon the trigonometric limits we derived in another section. To remind you, those are copied here.
To get through this section, you'll need to be familiar with analytic trigonometry, the derivative and the chain rule.
$$\lim_{x\to 0} \frac{\text{sin}(x)}{x} = 1$$
and
$$\lim_{x\to 0} \frac{\text{cos}(x)-1}{x} = 0$$
The derivative of $f(x) = \text{sin}(x)$
We start, as usual with the difference-quotient expression of the derivative:
$$\frac{d}{dx} sin(x) = \lim_{h\to 0} \frac{sin(x + h) - sin(x)}{h}$$
Now we recall the trigonometric sum identities:
$$ \begin{align} \text{sin}(a + b) = \text{sin}(a)\text{cos}(b) + \text{cos}(a)\text{sin}(b) \\[5pt] \text{cos}(a + b) = \text{cos}(a)\text{cos}(b) - \text{sin}(a)\text{sin}(b) \end{align}$$
We use the first to make a substitution for $\text{sin}(x+h)$,
$$= \lim_{h\to 0} \frac{\text{sin}(x)\text{cos}(h) + \text{cos}(x)\text{sin}(h) - \text{sin}(x)}{h}$$
Now factor a $\text{sin}(x)$ out of two of the terms of the numerator, like this:
$$= \lim_{h\to 0} \frac{\text{sin}(x)[\text{cos}(h) - 1] + \text{cos}(x)\text{sin}(h)}{h}$$
Now let's use the properties of limits to separate that expression into two different limits:
$$ = \lim_{h\to 0} \frac{\text{sin}(x)[\text{cos}(h) - 1]}{h} + \lim_{h\to 0} \frac{\text{cos}(x)\text{sin}(h)}{h}$$
Because $\text{sin}(x)$ and &\text{cos}(x)$ are continuous over their whole domains, we can remove them from the limit expression, which leaves us with the familiar and easy-to-evaluate trigonometric limits:
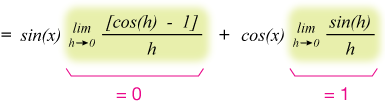
The derivative of the sine function is thus the cosine function:
Take a minute to look at the graph below and see if you can rationalize why cos(x) should be the derivative of $\text{sin}(x)$. Notice that wherever $\text{sin}(x)$ has a maximum or minimum (at which point the slope of a tangent line would be zero), the value of the cosine function is zero. Notice that wherever $\text{sin}(x)$ has maximum slope (where it passes through y=0), the cosine function reaches its minimum or maximum at ±1.

The derivative of $f(x) = \text{cos}(x)$
We find the derivative of $f(x) = \text{cos}(x)$ in a similar manner, and I'll work through the whole thing again here. Start with the difference quotient expression,
$$\frac{d}{dx} \text{cos}(x) = \lim_{h\to 0} \frac{\text{cos}(x + h) - \text{cos}(x)}{h}$$
then replace $\text{cos}(x + h)$ with $\text{cos}(x)\text{cos}(h) - \text{sin}(x)\text{sin}(h)$:
$$= \lim_{h\to 0} \frac{\text{cos}(x)\text{cos}(h) - \text{sin}(x)\text{sin}(h) - \text{cos}(x)}{h}$$
Now move the common factor $\text{cos}(x)$ and rewrite the numerator:
$$= \lim_{h\to 0} \frac{\text{cos}(x)[\text{cos}(h) - 1] - \text{sin}(x)\text{sin}(h)}{h}$$
Split the expression into two limits:
$$= \lim_{h\to 0} \frac{\text{cos}(x)[\text{cos}(h) - 1]}{h} - \lim_{h\to 0} \frac{\text{sin}(x)\text{sin}(h)}{h}$$
and remove the non h-dependent expressions to find our familiar trigonometric limits:
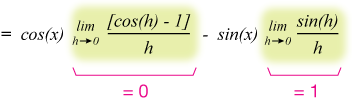
This time we get
Look again at the graphs of $f(x) = \text{cos}(x)$ and $f'(x) = -\text{sin}(x)$, and see if you can rationalize for yourself why $-\text{sin}(x)$ is the derivative of $\text{cos}(x)$.

The derivative of $f(x) = \text{tan}(x)$
For this derivative, we'll use the definition of the tangent and the quotient rule to find the result. You can use the difference quotient yourself in an exercise below.
$$\frac{d}{dx} \text{tan}(x) = \frac{d}{dx} \frac{\text{sin}(x)}{\text{cos}(x)}$$
We start by writing $\text{tan}(x)$ as $\text{sin}(x)/\text{cos}(x)$, then using the quotient rule:
$$= \frac{\text{cos}(x) \frac{d}{dx}\text{sin}(x) - \text{sin}(x) \frac{d}{dx}\text{cos}(x)}{\text{cos}^2(x)}$$
After taking the derivatives of $\text{sin}(x)$ and $\text{cos}(x)$ (which we can do now!), we recognize the Pythagorean identity: $\text{cos}^2(x) + \text{sin}^2(x) = 1$:
$$= \frac{cos^2(x) + sin^2(x)}{cos^2(x)}$$
If we recognize that $\text{sin}^2(x) + \text{cos}^2(x) = 1$, and that $1/\text{cos}^2(x)$ is $\text{sec^2(x)
$$= \frac{1}{\text{cos}^2(x)} = \text{sec}^2(x)$$
The result is:
Use the graph below to understand why $\text{sec}^2(x)$ gives the slope of $\text{tan}(x)$ at any point between ±$\pi$/2 (remember that the tangent function is infinite at multiples of ±$\pi/2$). Notice that the slope of the tangent function is always positive, and the value of the derivative is always positive, too.

Derivatives of the trigonometric functions
Here are the derivatives of the six trigonometric functions. You should commit the derivatives of $\text{sin}(x)$, $\text{cos}(x)$ and $\text{tan}(x)$ to memory.
$$ \begin{align} \frac{d}{dx} \text{sin}(x) &= \text{cos}(x) \\[5pt] \frac{d}{dx} \text{cos}(x) &= -\text{sin}(x) \\[5pt] \frac{d}{dx} \text{tan}(x) &= \text{sec}^2(x) \end{align}$$
$$ \begin{align} \frac{d}{dx} \text{sec}(x) &= \text{sec}(x)\text{tan}(x) \\[5pt] \frac{d}{dx} \text{csc}(x) &= \text{csc}(x)\text{cot}(x) \\[5pt] \frac{d}{dx} \text{cot}(x) &= \text{csc}^2(x) \end{align}$$
Practice problems
Calculate the derivatives of these trigonometric and mixed functions. Don't forget the product rule, the quotient rule and the chain rule.
-
$f(x) = 2x \, \text{sin}(x)$
Solution
$$f'(x) = 2 sin(x) + 2x cos(x)$$
-
$f(x) = \frac{3x^2}{\text{cos}(x)}$
Solution
$$f'(x) = \frac{6x cos(x) + 3x^2 \text{sin}(x)}{\text{cos}^2(x)}$$
-
$f(x) = \text{sin}^2(x)$
Solution
$$f'(x) = 2 \text{sin}(x) \text{cos}(x)$$
-
$f(x) = \text{tan}^4(x)$
Solution
Remember that $\text{tan}^4(x)$ means $[\text{tan}(x)]^4$.
$$ \begin{align} f'(x) &= 4[\text{tan}^3(x)]^3 \text{sec}^2(x) \\[5pt] &= 4 \text{tan}^3(x) \text{sec}^2(x) \end{align}$$
-
$f(x) = \frac{\text{cos}^2(x)}{\text{tan}(x)}$
Solution
$$f' = \frac{-2\text{tan}(x)\text{cos}(x)\text{sin}(x) - \text{cos}^2(x)\text{sec}^2(x)}{\text{tan}^2(x)}$$
-
$f(x) = \text{sec}(x)$
Solution
$$ \begin{align} f'(x) &= \frac{\text{cos}(x)(0) + \text{sin}(x)}{\text{cos}^2(x)} \\[5pt] &= \frac{1}{\text{cos}(x)}\cdot\frac{\text{sin}(x)}{\text{cos}(x)} \\[5pt] &= \text{sec}(x) \text{tan}(x) \end{align}$$
-
$f(x) = \text{csc}(x)$
Solution
$$ \begin{align} f'(x) &= \frac{\text{sin}(x)(0) + \text{cos}(x)}{\text{sin}^2(x)} \\[5pt] &= -\frac{1}{\text{sin}(x)}\cdot\frac{\text{cos}(x)}{\text{sin}(x)} \\[5pt] &= -\text{csc}(x) \text{cot}(x) \end{align}$$
-
$f(x) = \sqrt{x} \; \text{cos}(x)$
Solution
$$ \begin{align} f'(x) &= \frac{1}{2} x^{-1/2} \text{cos}(x) - \sqrt{x} \text{sin}(x) \\[5pt] &= \frac{\text{cos}(x)}{2 \sqrt{x}} \end{align}$$
-
$f(x) = \text{sin}(2x^2 - x^4)$
Solution
$$ \begin{align} f'(x) &= \text{cos}(2x^2 - x^4)(4x - 4x^3) \\[5pt] &= 4x (1 - x^2) \text{cos}(2x^2 - x^4) \end{align}$$
-
$f(x) = \text{cos}(\text{sin}(x))$
Solution
$$f'(x) = -\text{sin}(\text{sin}(x))\text{cos}(x)$$

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.