Velocity is speed with a direction
In physics, we often associate a direction with physical quantities. For example, it's nice to know the direction in which an object is moving or in what direction a force is applied to an object. To do this, we employ the concept of vectors. I strongly suggest that if you have not, you take a look at the vectors section before working through this one. It's absolutely crucial in physics to have a good working understanding of vectors.
$$\text{velocity} = \frac{\text{distance}}{\text{time}}$$
$$v = \frac{d}{t}$$
Just like speed, this is an average velocity over time t. We cannot know anything about the velocity (or speed) at any instant in time from this definition.
Velocity is the vector version of speed. Velocity is speed with a specified direction.
A velocity vector is an arrow that points in the direction of motion and has a length proportional to the speed. We call the speed the magnitude (size) of the velocity vector.

The only two things of importance about vectors is length (magnitude) and direction. Velocity vectors can be moved around in a plane or in 3-D space at will for the convenience of making calculation easier, so long as length and direction aren't affected.
A word about vector notation
Often in textbooks, vectors are denoted by symbols either in bold-face or with an arrow overhead, so the velocity vector would be v or v→. I am going to choose not to use any special notation for vectors throughout these notes. It will not only make the writing simpler, but it also forces the reader to be mindful about what is going on ... what's a vector and what is not ? ("not vectors" are "scalars"). That kind of mindfulness—about what is physically happening, is a key to success in physics.
Why velocity vectors?
The beauty of the velocity vector is that it lets us take velocity in any arbitrary direction and split it (or resolve it) into components that lie along (are parallel to) the axes of our coordinate system. Let the vector v, below, be a velocity vector:

Now let's resolve vector $\vec v$ into its components along each of the coordinate ($x$ & $y$) axes. We do this in two steps:
1. Move the vector to the origin
2. Find the components, $v_x$ and $v_y$ along the $x$ and $y$ axes.
Here's how it looks on the graph:

Notice that the vector sum of $v_x$ and $v_y$, added in either order because vector addition is commutative, is just our velocity vector $\vec v$.
This method of decomposing vectors into two new vectors aligned with our coordinate axes will be invaluable as you continue to study physics, so learn it well. Re-read the vectors notes if you need to.
Vectors vs. scalars
Velocity is a vector and speed is a scalar. Speed is the length of the velocity vector, calculated using the Pythagorean theorem:

A vector has length and direction, a scalar is just a number.
Speed is the length (also called "magnitude" or "modulus") of the velocity vector.
Relation to the kinematic equations
It's worth taking a minute to relate the expression for average velocity,
$$\bar{v} = \frac{v_i + v_f}{2},$$
to one of the so-called kinematic equations. These form a set of four; they are
$$ \begin{matrix} (1) && v = v_0 + at \\[5pt] (2) && \color{#E90F89}{\Delta x = \left( \frac{v + v_0}{2} \right) t} \\[5pt] (3) && \Delta x = v_0 t + \frac{1}{2} at^2 \\[5pt] (4) && v^2 = v_o^2 + 2 a \Delta x \end{matrix}$$
Often in physics courses, these equations are introduced early, and then used to solve most problems of motion. Unfortunately, this can lead to a "formula first" approach instead of one that seeks to understand the physical principles.
I prefer a different approach that addresses each problem from basic principles, so that you'll develop a better idea of what's actually physically happening in each problem you encounter. After enough practice, you'll likely develop the kinematic equations on your own.
Let's look at the highlighted kinematic equation (2),
$$\Delta x = \left( \frac{v + v_0}{2} \right) t$$
Notice that it's just the equation distance = average velocity × time. For any smooth acceleration (change in velocity), the distance moved is just the average of the beginning and ending velocities multiplied by the time to achieve the change.
The definition of velocity, $v = \frac{d}{t}$, is always an average over time.
Vector resolution: special triangles
We know that two vectors can be added to form a third. Often we'd like to do that in reverse: to take a vector that lies at an odd angle to the normal $x-y$ (Cartesian) grid, and resolve it into the sum of two vectors, one along the x-axis and one along the $y$-axis. Here's a picture of what we mean:

The process of resolving a vector is to first move it to the origin (remember, this can easily be done because the only things that matter about a vector are length [magnitude] and direction), and second, to find vectors $v_x$ and $v_y$, which lie along the $x$- and $y$-axes, that sum to $\vec v$.
The problem with vector resolution, for some of you, is that you don't yet have any experience with trigonometry (sines, cosines and all that).
But don't worry, there are a few angles (the angle between vector v and the x-axis) that you can work with without knowing trigonometry. These are found in the so-called special triangles: 45-45-90 and 30-60-90 (degrees). We'll go through those below.
The 45-45-90 triangle
The 45-45-90 triangle is just what it sounds like, a right triangle that has two 45˚ angles, and is thus an isoceles triangle. We'll work with just symbols for the lengths of the sides, like this:

Now the Pythagorean theorem has to hold for this right triangle, so
$$x^2 + x^2 = r^2$$
Now combine the like terms on the left,
$$2x^2 = r^2$$
and let's solve for $x$ (you'll see why in a minute), by first dividing both sides by 2.
$$x^2 = \frac{r^2}{2}$$
Now to solve for $x$, take the square root of both sides:
$$x = \sqrt{\frac{r^2}{2}}$$
Taking the square root of the numerator gives $r$, with $\sqrt{2}$ in the denominator:
$$x = \frac{r}{\sqrt{2}}$$
Finally, just for completeness, not that it really matters mathematically, the denominator of such an equation is usually "rationalized" by multiplying by $\sqrt{2} / \sqrt{2}$:
$$x = \frac{r\sqrt{2}}{2}$$
Now imagine if we let r, the length of the hypotenuse of our triangle, be 1. Then we get this triangle, complete with side measures:
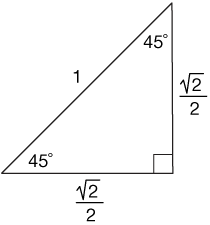
What's great about such a triangle, is that it will give us the lengths of the sides of a 45-45-90 triangle with any hypotenuse length because we have the ratios of the side lengths —1:$\sqrt{2}/2$. Here are some practice problems to help you figure it out.
Practice problems 1
| 1. | The hypotenuse of a 45-45-90 triangle is 81 cm long. What must be the length of the legs of this triangle? | |
| 2. | A cannon is fired upward at a 45˚ angle and with an initial velocity of 75 m/s. Calculate the initial velocity components parallel to and perpendicular to the ground. | |
| 3. | A car is traveling away from a viewer at a 45˚ angle to the road she's on. That car will appear to get smaller, a result of the component of its velocity in the direction of the viewer's gaze, and it will appear to move left to right, a result of the component of its velocity from left to right. What speed must the car be traveling in order for its left-right apparent velocity to be 45 mi./h? |
The 30-60-90 triangle
The 30-60-90 (degrees) right triangle is another frequently-encountered triangle that's worth knowing a lot about.

It isn't quite as easy to find an expression for the side lengths $x$ and $y$, unless we combine two of these triangles to form an equilateral triangle like this:

Notice here that I've replaced $x$ from the original figure with r/2. We know that the gray vertical line both bisects the top 60˚ angle (by construction) and bisects the base of the triangle. For a proof the the angle bisector of an isosceles triangle also bisects the opposite side, click here.
Now we can set up the Pythagorean theorem for one of the two 30-60-90 triangles shown:
$$r^2 = y^2 + \left( \frac{r}{2} \right)$$
Squaring the last term gives
$$r^2 = y^2 + \frac{r^2}{4}$$
Let's solve for y in terms of r by separating terms across the = sign:
$$y^2 = r^2 - \frac{r^2}{4}$$
The difference on the right is easy to calculate; just use 4 as a common denominator:
$$y^2 = \frac{3 r^2}{4}$$
Now taking te square root of both sides gives
$$y = r \, \frac{\sqrt{3}}{2}$$
Now if we take $r = 1$, we arrive at the prototype 30-60-90 triangle:

$$$$
So for a 30-60-90 triangle, the shorter leg (recall that the sides that form the right angle of a right triangle are called "legs") has a length that is half the length of the hypotenuse, and the longer leg is $\sqrt{3}{2}$ of the hypotenuse.
Practice problems 2
| 1. | The hypotenuse of a 30-60-90 triangle measures 23 m. Calculate the lengths of the other two sides of this right triangle. | |
| 2. | A baseball is thrown upward at an angle of 30˚ relative to the ground and a velocity of 25 m/s. Calculate the forward component of the velocity of the ball. | |
| 3. | A 30 ft. ladder leans against a tall building, forming a 60˚ angle with the ground. At what vertical height (in feet) does the ladder touch the wall? |
The special triangles.
45-45-90

30-60-90

Practice problems 3
These vector velocity problems can be solved using basic vector knowledge and the special triangles (no trigonometry required).
| 1. | How fast can an airplane, with a maximum speed of 160 Km/h in still air, travel 250 miles if it has a steady headwind of 15 Km/h ? | |
| 2. | Two cars begin a trip together, one traveling at 65 mi./h, and the other at 75 mi./h on the same freeway. After how many miles will the slower car be 1 hour behind the faster? | |
| 3. | A projectile is fired upward at an angle of 45˚ with an initial velocity of 30 m/s. Calculate the magnitude of the component velocity vectors along the ground and straight up (x and y, respectively). | |
| 4. | On a windless day, a boat can travel at a maximum forward speed of 10 knots. It travels across a lake on a day with a 5-knot cross wind (perpendicular to the intended direction of travel) from the right. Calculate the actual speed of the boat (in knots) and its deviation (in degrees) from its intended course |
More vector resolution: Trigonometry
Finally, and more often, we need to resolve a vector of known magnitude that forms an angle with the x- or y-axes that is not a 30˚, 45˚ or 60˚ angle. For that we use simple right-triangle trigonometry, and, if necessary, non-right angle trig.
Resolving a vector
Here is a quick example of how trigonometric relationships can allow us to find the $x$ and $y$ components of any vector, as long as the angle of the vector, relative to the axis system, is known. By the way, this idea is completely generalizable to 3-D (or higher!) dimensions.
Consider the vector v rotated 27˚ from the $x$-axis:

Now we'll decompose this vector into two component vectors along the x- and y-axes.

Using basic right triangle trigonometry, we can calculate $v_x$:
$$ \begin{align} V_x &= v\cdot \cos(\theta) \\[5pt] &= 25 \cdot \cos(27^{\circ}) \\[5pt] &= 22.3 \; m/s \end{align}$$
Similarly, we calculate $v_y$:
$$ \begin{align} V_y &= v\cdot \sin(\theta) \\[5pt] &= 25 \cdot \sin(27^{\circ}) \\[5pt] &= 11.3 \; m/s \end{align}$$
So if you were standing at the origin, this object would be moving to the right at 23.3 m/s, and upward at 11.3 m/s.
Finding a vector from components
When we already have all vector components (two in the case of a 2D vector, which we'll be working with mostly), it's easy to find the length of the vector using
$$v = \sqrt{|v_x|^2 + |v_y|^2}$$
where $|v_x|$ and $|v_y|$ are the lengths of components $v_x$ and $v_y$, respectively.
The angle of the vector can be calculated using the inverse tangent function. Let's use the method to undo our previous example. Take a vector with components $v_x$ and $v_y$. Here's the drawing:

The tangent of the angle is (opposite over adjacent):
$$\tan(\theta) = \frac{v_x}{v_y}$$
To find the angle, it's a straightforward matter to take the inverse tangent of both sides, yielding
$$ \begin{align} \theta &= \tan^{-1} \left( \frac{v_x}{v_y} \right) \\[5pt] &= \tan^{-1}\left( \frac{11.3}{22.3} \right) \\[5pt] &= 27˚ \end{align}$$
So we can use right triangle trigonometry to both resolve and reconstruct vectors.
Non-right triangles
Finally, once in a while we can't work with a nice right triangle. That's fine, because we have the law of sines and the law of cosines for those. I'll save the examples for the problems below, but just to recap, here are the LOS and LOC:
LOS
$$\frac{\sin(A)}{a} = \frac{\sin(B)}{b} = \frac{\sin(C)}{c}$$
LOC
$$ \begin{align} c^2 &= a^2 + b^2 - 2ab \, \cos(C) \\[5pt] b^2 &= a^2 + c^2 - 2ac \, \cos(B) \\[5pt] a^2 &= b^2 + c^2 - 2bc \, \cos(A) \end{align}$$
where capital letters represent angles and lower-case letters are the corresponding sides opposite those angles, as usual.
Examples: Airplane velocity vectors
Consider an airplane that can travel at a speed of 150 Km/h in still air. That would give it a velocity vector of 150 Km/h in length pointed in its direction of travel. Now add in a 30 Km/h headwind. The situation is shown below. The net forward velocity of the plane is the sum of 150 Km/h and -30 Km/h, or 120 Km/h in the direction of travel.

Now let's turn that headwind into a tailwind, or pushing wind. The vector diagram is shown below. This time the 30 Km/h wind vector adds to the velocity of the plane, for a total velocity of 180 Km/h.

That's why a flight across the United States from west to east is usually faster than a flight from east to west. The prevailing (dominant) wind moves from west to east.
Now let's get a little fancier. How about a cross-wind, or a wind that comes from 90˚ from the direction of travel – from the right or left.
To add these two vectors, just use the Pythagorean theorem. You can see that the direction of travel will be slightly to the right of where the plane is steering, and it's velocity will be 6 Km/h faster than without the crosswind.

Finally, let's let the wind hit the plane at an odd angle, so that if we want the new velocity vector, we have to solve a law of cosines problem. If you don't know the LOC, don't worry about it right now.

This is basically how we navigate planes without more sophisticated equipment like radio and radar.
Practice problems 4
These vector velocity problems require some trigonometry to solve. Give them a try if you've aready studied trig. Otherwise, it's OK to skip them.
| 1. | A jet flies at 600 Km/h in still air at maximum power. The same jet using maximum power to fly due west (270˚ on the compass), flies into a 100 Km/h northwest wind that makes a 23˚ angle with the intended path (293˚ on the compass. Find the actual velocity of the plane. | |
| 2. | If a swimmer can swim at 0.5 m/s in still water, how long will it take her to swim across a 50 m-wide river flowing at 0.5 m/s? Assuming she swims perpendicular to the flow of the river, how far downstream will she be when she reaches the shore? | |
| 3. | A projectile is launched with an initial velocity of 29 m/s and at an angle of elevation with respect to the ground of 39˚. Calculate the component of the projectile velocity parallel to the ground. | |
| 4. | A plane flies with a velocity of 53 m/s east (90˚ on the compass), encountering a 10 m/s crosswind from 10˚ (that's 10˚ to the 'right' of north, which is 0˚). Calculate the magnitude and direction (relative to due north, 0˚) of the resultant velocity at which it travels. |

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.













