This section will refer to several mathematical models of waves. These are discussed in the Mathematics of Waves section. You might want to review that section before continuing with sound waves.
What is a sound wave?

The illustration above is a schematic representation of air molecules (blue spheres). Gas molecules aren't ever organized in nice rows and columns like that, but it helps for the diagram.
A sound wave is a periodic disturbance in a medium like air, though sound can also travel through liquids and solids — more on that later.
A. Sound is generated by vibration of something, like your vocal chords, a tuning fork or a piano string. As a vibrating object moves, it periodically pushes on the surrounding air molecules, causing them to move and compress.
B. One such compression zone has been formed by a mechanical vibration on the left, and will now begin to move or propagate to the right. Particles that have received a push from the left will push on particles to the right, and the compression zone moves along.
In panels C and D, the wave continues to propagate. The zones of high density gas are called compression zones and the zones of relatively low density in between are called rarefaction zones.
E. A new compression zone has been formed and will continue to propagate to the right. The distance between compression zones is the wavelength of the wave.
The disturbance in the medium (air) is in the same direction as the direction of the wave, so sound waves are called longitudinal waves. The disturbance is along the direction of travel. This is in contrast to transverse waves like water waves, in which the disturbance in the medium is at right angles to the direction of travel.
The diagram below is another common way of illustrating compression and rarefaction in sound waves.
Wave motion comes in two forms. In longitudinal waves (sound waves), the disturbance in the medium is in the direction (along) the wave. In transverse waves the disturbance is at right angles to the direction of the wave. Water waves created by tossing a pebble in a smooth pond spread out horizontally from the center, but the actual disturbance in the water is up and down.
Another representation of longitudinal waves

The spacing between vertical lines represents the average spacing between air molecules. In the top row, a compression zone has been formed and will travel to the right. If the physical object causing the disturbance is periodic, like a vibrating tuning fork, compression zones will continue to form at even intervals of time and distance (the wavelength). When something like the human ear experiences such a periodic compression wave, and if its wavelength is within the range of human hearing, it will be experienced as a sound.

Representation with sine waves
We've seen that sound waves are periodic alternations in compression and rarefaction of air. Because of their periodic nature, and even though they aren't actually transverse waves, it's still convenient to represent them with sine waves.

All of the features of a sound wave map onto the sine wave:
- The amplitude of a sound wave corresponds to the volume or intensity of the sound.
- The frequency or wavelength correspond to the pitch of the sound,
- and relative phase is important for sound waves. Sounds can interfere, and even cancel, if they are produced out of phase.
The relationship λ · ν = speed also holds for sound waves. The speed of sound in air and several materials are listed in this table:
| Material | Speed (m/s) |
|---|---|
| Rubber | 60 |
| Air (40˚C) | 355 |
| Air (20˚C) | 343 |
| Lead | 121- |
| Gold | 3240 |
| Glass | 4520 |
| Aluminum | 6320 |
Sound transmission through solids & liquids
Sound travels faster through liquids and solids than through air. That's not too hard to understand, given the nature of a sound wave in air.
Sound traveling through air depends on collisions of particles. In air, those particles are widely spread out compared to the particles of a liquid or solid, so there is a time delay between collisions, resulting in a slower propagation of the wave.
In liquids and solids, the atoms and molecules are much closer together, thus the time between collisions is reduced, resulting in faster sound-wave travel. Sound travels nearly 20 times faster through a bar of aluminum than through air, for example (see the table above for some representative speeds of sounds in air, liquids and solids).
Sound travels at 1484 m/s in pure water, more than four times faster than through air, but not as fast as in a metal, where the atoms are even more tightly-packed.
Effect of density
The speed of sound in a medium is apparently proportional to the density of the medium. The more space between particles of some mass, the slower the speed of sound in that medium. That's evident in the speeds of sound in air, water and metal. But how do density changes in one type of medium affect the speed of sound waves?
In solids and liquids, the speed of sound scales as the reciprocal of the square root of the density:
$$\text{speed} \propto \frac{1}{\sqrt{\rho}}$$
where ρ (rho) is the Greek symbol for density. Clearly, as the density increases, the speed decreases. Why?
It's because higher density means more mass in a given volume. That means heavier gas particles, which have more inertia and are harder to accelerate as the wave propagates, resulting in a slower wave.
Gases
It's a little different for gases. When a gas is heated at constant pressure (think of atmospheric pressure), the molecules speed up and have harder collisions, creating more space between them and a lower density. We'd expect to see a reduced speed of sound in a hotter gas, but this is what we actually see:

This is where science gets fun — when we don't get the expected results. The reason for this is that the faster speeds of hotter gas particles hasten collisions, and thus hasten the propagation of sound waves.
Range of human hearing & the ear
The human ear (when reasonably young) can hear sounds at frequencies between 20 Hz and 20 KHz, or between wavelengths of 17 m and 1.7 cm.
When humans age, the mechanism of hearing deteriorates, particularly on the high-frequency end of the scale. Older adults lose the ability to hear very high frequencies starting at about age 50 or so. That's why kids can set their phone alerts at high frequency and hear the tone when their parents (or teachers) can't.
The ear
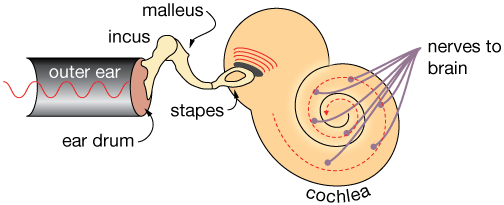
It's worth taking a look at how the ear works, because it's pretty ingenious. The diagram below is a highly schematic version of the ear, but the essential features important for hearing are all there.
Sound waves enter the ear through the outer ear or the auditory canal, and hit a thin, tightly-stretched membrane, the ear drum (tympanic membrane). Sounds cause the drum to vibrate.
On the other side of the drum, which separates the outer ear from the inner ear, are three small bones
– the smallest in the body, the incus, malleus and stapes, commonly referred to (because of their shapes) as the hammer, anvil and stirrup, respectively.
The hammer is connected to the inner side of the drum, and thus vibrates when the drum does. Acting like a series of levers, the hammer, anvil and stirrup amplify the vibrations of the drum.
The stirrup is in contact with fluid (mostly water) in the snail-shaped cochlea. The cochlea (the word comes from Greek and Latin and means "spiral.") is an ingenious device for separating frequencies of sound. Lower pitched (long wavelength) sounds travel all the way through the spiral of the cochlea and are picked up by nerve endings there, while higher-frequency sounds don't get as far before being translated into a nerve impulse.
The auditory nerves lead to the brain where sounds are processed and perceived.
The ear is a transducer, a device that converts mechanical sound waves (longitudinal waves that impart kinetic energy to the ear drum) to electrical signals in the brain.
Microphones and speakers

It's not surprising that a microphone works in a way very similar to a biological ear (see diagram). When sound hits a microphone, it vibrates a thin membrane, usually a plastic or metal foil. A wire coil is coupled to that membrane in one of a variety of ways.
A permanent magnet is inserted into the coil, and the coil moves back and forth across the magnet as the membrane responds to sound.
We know (or you will eventually study) that when a coil of wire is moved through a magnetic field, a current is generated in the wire through electromagnetic induction. The two ends of the wire forming the coil are fed to an amplifier circuit which converts the current to a useful signal, say for broadcasting or recording.
Speakers work in a similar way, just in reverse. An amplifier circuit delivers a current through a coil of wire, which produces a small magnetic field that alternatively opposes and aligns with the field of a permanent magnet. This produces a motion in the coil, which in turn vibrates a membrane, a reed or a large paper or fabric cone, depending on the range of pitches that the speaker is designed to produce.

Practice problems
| 1. |
The average human can hear sounds between frequencies of 20 Hz and 20 KHz. Assuming that the speed of sound in air is 340 m/s, calculate the wavelengths of these waves in meters. SolutionFirst, let's rearrange our wave formula to solve for wavelength (λ): $$ \begin{align} \lambda \nu &= \text{speed} \\[5pt] \lambda &= \frac{\text{speed}}{\nu} \end{align}$$ Now the wavelengths are: $$ \require{cancel} \begin{align} \lambda_{20} &= \frac{340 \frac{m}{\cancel{s}}}{20 \frac{1}{\cancel{s}}} = \color{red}{17 \, m} \\[8pt] \lambda_{20,000} &= \frac{340 \frac{m}{\cancel{s}}}{20,000 \frac{1}{\cancel{s}}} = 0.017 \, m \\[5pt] &= \color{red}{17 \, mm} \end{align}$$ |
| 2. |
Calculate the frequency of a sound wave with a length of 23 cm, traveling through air at 340 m/s. SolutionFirst, 23 cm is 0.23 m. If you don't know that, remember that your unit conversion strategy always works: $$23 \, \cancel{cm} \left( \frac{1 \, m}{100 \, \cancel{cm}} \right) = 0.23 \, m$$ (of course, it helps to remember your metric prefixes!) Now to rearrange our wave formula to solve for frequency (ν): $$\lambda \nu = \text{speed} \color{magenta}{\longrightarrow} \nu = \frac{\text{speed}}{\lambda}$$ Now the frequency is $$ \begin{align} \nu &= \frac{\text{speed}}{\lambda} \\[5pt] &= \frac{340 \frac{\cancel{m}}{s}}{0.23 \cancel{m}}= \color{red}{1478 \, Hz} \end{align}$$ |
| 3. |
The pitch of sound can change when it propagates through different materials. Take a sound wave with a wavelength of 50 cm. Calculate its frequency as it travels through air (s = 340 m/s), water (s = 1418 m/s) and aluminum (Al, s = 6320 m/s) SolutionFirst, 50 cm is 0.50 m. If you don't know that, remember that your unit conversion strategy always works: $$50 \, \cancel{cm} \left( \frac{1 \, m}{100 \, \cancel{cm}} \right) = 0.50 \, m$$ Now to rearrange our wave formula to solve for frequency (ν): $$\lambda \nu = \text{speed} \color{magenta}{\longrightarrow} \nu = \frac{\text{speed}}{\lambda}$$ Our three calculations are: $$ \begin{align} \nu_{air} &= \frac{340 \frac{\cancel{m}}{s}}{0.50 \cancel{m}}= \color{red}{780 \, Hz} \\[5pt] \nu_{water} &= \frac{1418 \frac{\cancel{m}}{s}}{0.50 \cancel{m}}= \color{red}{2,836 \, Hz} \\[5pt] \nu_{Al} &= \frac{6320 \frac{\cancel{m}}{s}}{0.50 \cancel{m}}= \color{red}{12,640 \, Hz} \\[5pt] \end{align}$$ The pitch of this sound would be higher in water and higher still when transmitted through a piece of aluminum. |
| 4. |
A person stands far away from a high cliff wall and shouts at it. If she times how long it takes her voice to travel to the wall, bounce back (echo) and return to her ears, obtaining 2.8 seconds for the round trip, how far away is the cliff. Assume that the speed of sound in air is 340 m/s. SolutionThis is a speed-distance-time problem in which we're trying to find distance, so we have $$s = \frac{d}{t} \color{magenta}{\longrightarrow} d = st$$ The round-trip distance is $$d = st = 340 \frac{m}{\cancel{s}} \cdot 2.8 \, \cancel{s} = \color{red}{952 \, m}$$ The distance to the cliff is half of that, or |
| 5. |
The mean distance to the moon from Earth is 382,500 Km. If a sound was made on the moon, how long (in hours) would it take for it to reach Earth? SolutionThis is a trick question. Sound needs a medium in which to travel. Any atmosphere on the moon is far too thin to transmit sound, and the space between the moon and Earth is virtually empty of matter. It's like the tag-line to the movie "Alien" said: "In space, no one can hear you scream." |
Measuring volume
If you don't have any experience with logarithms or logarithmic functions, you can skim this section of this page. Just take decibels to be a unit of sound intensity and leave it at that. Do make sure to take a look at the table of dB levels of some common sounds below, though, so you're familiar with the range of the unit.
The loudness or intensity of a sound is measured in a unit called decibels (dB).
| Sound | dB | Response |
|---|---|---|
| Hearing threshold |
0 dB | |
| Normal breathing | 10 dB | No harm |
| Whisper | 30 dB | No harm |
| Normal conversation | 60 dB | No harm |
| Washing machine dishwasher |
70 dB | Annoyance |
| Gas-powered lawnmower, leaf blower |
80 dB | Damage after 2 hours |
| Loud motorcycle | 95 dB | Damage after less than 1 h |
| Train horn crowd noise |
100 dB | Hearing loss possible |
| Maximum | > 105 dB | Hearing loss in 5 minutes |
Table adapted from the U.S. CDC.
Decibels as a unit
The decibel unit was originally used to measure amplification of telephone signals in the early days of phone communication. The bel was named after telephone inventor Alexander Graham Bell. Because it turned out to be a somewhat large unit, the decibel (1/10 of a bel) was more widely used. It is the standard way to measure signal noise and amplification today.
The decibel is used to measure sound levels, but also to measure how much electronic signals are amplified or attenuated. It is a logarithmic unit in this sense:
Imagine that there are two stereo speakers, one playing sound with power P1 and the other with P2. Let's say that P2 > P1. In decibels, the difference in the sound level between the two speakers is
$$10 \cdot log_{10} \left( \frac{P_2}{P_1} \right) \, dB$$
If P2 = 2P1 (speaker 2 uses twice the power of speaker 1), then our difference is:
$$10 \cdot log_{10} \left( \frac{P_2}{P_1} \right) = 10 log_{10} (2) \approx 3 \, dB.$$
If speaker 2 uses ten times the power of speaker 1, then we'd have
$$10 \cdot log_{10} \left( \frac{P_2}{P_1} \right) = 10 log_{10} (10) = 10 \, dB.$$
Here is a table of some decibel values given the ratio P2/P1:
| P1/P2 | 10 log10(P2/P1) |
|---|---|
| 2 | 3 |
| 5 | 7 |
| 10 | 10 |
| 100 | 20 |
| 1,000 | 30 |
| 10,000 | 40 |
| 1,000,000 | 60 |
From the table you can see that for each factor of ten in the power ratio, we get another ten decibels.
The Greek alphabet
| alpha | Α | α |
| beta | Β | β |
| gamma | Γ | γ |
| delta | Δ | δ |
| epsilon | Ε | ε |
| zeta | Ζ | ζ |
| eta | Η | η |
| theta | Θ | θ |
| iota | Ι | ι |
| kappa | Κ | κ |
| lambda | Λ | λ |
| mu | Μ | μ |
| nu | Ν | ν |
| xi | Ξ | ξ |
| omicron | Ο | ο |
| pi | Π | π |
| rho | Ρ | ρ |
| sigma | Σ | σ |
| tau | Τ | τ |
| upsilon | Υ | υ |
| phi | Φ | φ |
| chi | Χ | χ |
| psi | Ψ | ψ |
| omega | Ω | ω |
propagate
To propagate in this context is to move forward and to spread out.
It can also mean to spread an idea or rumor, or to continue a plant or animal gene line in breeding.

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.