Finding the midpoint of a line segment
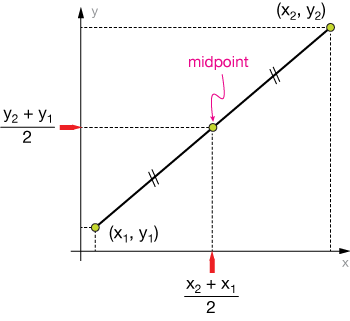
If you have the coordinates (x, y) of the endpoints of a line segment, finding the midpoint of the segment is very simple. Just take the average of the two x-coordinates of the endpoints (add them and divide by two) to get the x-coordinate of the midpoint. Then do the same with the y-coordinates.
The midpoint "formula" is given below. It implies that the x coordinate of the midpoint is half way between the x coordinates of the endpoints, and likewise for the y-coordinates. This is proven using triangle congruence below the formula.
Midpoint formula
The coordinates of the midpoint of a line segment on a plane (2-dimensional) are:
$$\text{midpoint} = \left( \frac{x_2 + x_1}{2}, \; \frac{y_2 + y_1}{2} \right)$$
Proof of the midpoint formula
If we take line segment AE (right →) with midpoint C, we can draw all of the dashed lines parallel to the coordinate axes. All vertical lines are || and all horizontal lines are ||. Now because parallel lines yield congruent pairs of corresponding angles (∠ 1 ≅ ∠ 3, ∠ 2 ≅ ∠ 4), we have that ΔABC ≅ ΔCDE by the ASA (angle-side-angle) theorem.
The congruence of those triangles means that segments AB and CD are congruent, thus B bisects AF, and BC ≅ DE, thus D bisects EF.
So the coordinates of C are x = the midpoint of AF (the average of the x-coordinates of A and E) and y = midpoint of ED (the average of the y-coordinates of A and B.

ASA
"Angle-Side-Angle" theorem
If two angles and the connecting side of one triangle are congruent to the corresponding two angles and connecting side of another, then the two triangles are identical

Practice problems
Calculate the midpoint of the segments with the following endpoints:
| 1. |
Solution$$ \begin{align} \text{mp} &= \left( \frac{-1 + 2}{2}, \frac{-2 + 2}{2} \right) \\ \\ &= \left( \frac{1}{2}, 0 \right) \end{align}$$ |
| 2. |
Solution$$ \begin{align} \text{mp} &= \left( \frac{-4+9}{2}, \frac{2-3}{2} \right) \\ \\ &= \left( \frac{5}{2}, \frac{-1}{2} \right) \end{align}$$ |
| 3. |
Solution$$ \begin{align} \text{mp} &= \left( \frac{-4+3}{2}, \frac{-4-4}{2} \right) \\ \\ &= \left( \frac{-1}{2}, -4 \right) \end{align}$$ |
| 4. |
Solution$$ \begin{align} \text{mp} &= \left( \frac{6-4}{2}, \frac{2+8}{2} \right) \\ \\ &= (1, 5) \end{align}$$ |
| 5. |
Solution$$ \begin{align} \text{mp} &= \left( \frac{-1-1}{2}, \frac{-5+2}{2} \right) \\ \\ &= \left( -1, \frac{-3}{2} \right) \end{align}$$ |
| 6. |
Solution$$ \begin{align} \text{mp} &= \left( \frac{6+6}{2}, \frac{20-4}{2} \right) \\ \\ &= \left( \frac{12}{2}, \frac{16}{2} \right) = (6, 8) \end{align}$$ |
7. Find the other endpoint of the segment with endpoint
Solution
The midpoint is
$$\left( \frac{-3 -x}{2}, \frac{-4 -y}{2} \right) = (2, 1)$$
This gives us an equation for the x-coordinate of the missing point, and one for the y. They are:
$$ \begin{align} \frac{-3 +x}{2} &= 2 \\ \\ -3 +x &= 4 \\ x &= 7 \end{align}$$
$$ \begin{align} \frac{-4 +y}{2} &= 1 \\ \\ -4 +y &= 2 \\ y &= 6 \end{align}$$
The point is (7, 6)
Extension to lines in 3 and higher dimensions
The midpoint idea can easily be extended to lines in three dimensions, where each point has a three-dimesional coordinate, like (x, y, z) or (-1, 2, 7). It looks like this:
$$\text{mp} = \left( \frac{x_1 + x_2}{2}, \; \frac{y_1 + y_2}{2}, \; \frac{z_1 + z_2}{2} \right)$$
And we can extend that to lines in many dimensions. Even though the look of such line segments might be difficult for you to imagine, they do exist, and each has a midpoint given by:
$$\text{mp} = \left( \frac{x_1 + x_2}{2}, \; \frac{y_1 + y_2}{2}, \; \frac{z_1 + z_2}{2}, \; \dots \right)$$

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2016, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.