Right-triangle trigonometry
The word trigonometry derives from the Greek for "triangle measure", and that's a pretty good description of the nuts and bolts of it. Still, that's not all there is to trigonometry — by a long way. Learning trig (we call it "trig") will crack the door open to a wide variety of other fields, including doing math on the complex plane, polar functions, and many applications in calculus and other fields.
If you're thinking about more advanced courses in math and science, in high school or in college, learn the basics of right-triangle trigonometry well. You won't regret it.
SOH—CAH—TOA
Shhhhh... mathematicians don't like this too much, but for most of you, about 80% of all you'll ever need to know about trig. is in that mnemonic: SOH-CAH-TOA.
Most of the trigonometry you'll ever need to do involves right triangles, though we'll generalize this to any triangle, and do a lot of other interesting things later. Take a look at the right triangles on the right so we can be on the same page with our terms.
Right triangles have a right angle, of course, and a hypotenuse across from that. We'll define an angle, θ (the Greek letter "theta"), and our choice of θ will determine the labels of the other two sides. The opposite side (o) is opposite angle θ, and the side that is a part of theta will be called the adjacent side (a).
Anatomy of a right triangle

Aside: Greek letters
If you study trigonometry or you move ahead in math or science, you'll need to be familiar with some Greek letters, mainly because we run out of letters with which to designate things. Take a look at the box (Greek to me). We'll use those letters a lot.
Greek to me
In the field of trigonometry, we often use Greek letters to label angles. Greek letters also come in handy in the sciences, where we run out of letters to represent physical quantities.
The most commonly-used Greek letters in trigonometry are
$$ \begin{matrix} \theta && \text{"theta"} \\ \phi && \text{"phi"} \\ \chi && \text{"chi"} \end{matrix}$$
The three major trigonometric functions are functions of the angle θ, and are ratios of the lengths of the sides of right triangles:
- Sine = Opposite over Hypotenuse (SOH),
- Cosine = Adjacent over Hypotenuse (CAH),
- Tangent = Opposite over Adjacent (TOA).
SOH—CAH—TOA
Pro tip: Very often we refer to trigonometry as "trig".
Trigonometric functions are just ratios of the lengths of sides of right triangles.
$$\text{sin}(\theta) = \frac{o}{h}$$
$$\text{cos}(\theta) = \frac{a}{h}$$
$$\text{tan}(\theta) = \frac{o}{a}$$
Example 1
Calculate the measures of the missing sides and angles of a right triangle.

That's plenty of information, though, to find all of the missing information.
To begin, just write down one of the trigonometric relationships — let's choose sine — and rearrange it to find the missing quantity:
$$\text{sin}(\theta) = \frac{o}{h} \color{#E90F89}{\longrightarrow} o = h \cdot \text{sin}(\theta)$$
So the side opposite the 25˚ angle has length
$$o = 10 \cdot \text{sin}(25^{\circ}) = 4.2 \; cm$$
There is now enough information to find the third (adjacent) side using the Pythagorean theorem, but let's use the cosine, just for practice:
$$\text{cos}(\theta) = \frac{a}{h} \color{#E90F89}{\longrightarrow} a = h \cdot \text{cos}(\theta)$$
And the length of the adjacent side is
$$a = 10 \cdot \text{cos}(25^{\circ}) = 9.1 \; cm$$
You can confirm this for yourself using the Pythagorean theorem.
Lastly, we can easily find the degree-measure of the missing angle,
$$\phi = 180^{\circ} - 25^{\circ} - 90^{\circ} = 55^{\circ}$$
Trig. functions & your calculator
Almost any calculator or calculator application (e.g. on your phone) will be able to calculate sine, cosine and tangent functions, and a few other trig. functions that we'll cover in due time. Calculators make the trig. functions act like "black boxes" — you just key in your angle and you get its sine, cosine or tangent.
You'll need to be careful about the units. Your calculator can use two units of angle measure: Degrees and Radians. Make sure you're working with the right units. Learn more about angle measurements here.

Example 2
Calculate all of the missing angles and sides of this triangle. This time the hypotenuse is one of the missing sides.

$$ \begin{align} \text{cos}(34^{\circ}) = \frac{18}{h} \color{#E90F89}{\longrightarrow} h &= \frac{18}{\text{cos}(34^{\circ})} \\[5pt] h &= 21.7 \; cm \end{align}$$
We can find the length of the opposite side, o, using the tangent function in a similar way:
$$ \begin{align} \text{tan}(34^{\circ}) = \frac{o}{18} \color{#E90F89}{\longrightarrow} o &= 18 \cdot \text{tan}(34^{\circ}) \\[5pt] o &= 12.1 \; cm \end{align}$$
So we have sides of 18 cm, 12.1 cm and 21.7 cm. We can easily check whether these are correct using the Pythagorean theorem:
$$ \begin{align} 21.7^2 &\stackrel{?}{=} 18^2 + 12.1^2 \\[5pt] 470.89 &= 324 + 146.41 \\[5pt] &= 470.41 \end{align}$$
The small amount of error, 0.48 cm, is just due to rounding off the earlier answers. Finally, the missing angle is just the complement of the 34˚ angle (the right angle accounts for the other 90˚ of a right triangle):
$$90^{\circ} - 34^{\circ} = 56^{\circ}$$
So we know everything there is to know about that triangle, even though we originally only knew the measures of two angles and one side.

Practice problems 1
Try to find all angle and side measurements of the three triangles below using SOH-CAH-TOA trig. Roll over the problems to see the answers.



Example 3
In the scenario below, a surveyor can calculate the height of a building by measuring the angle of elevation from her position to the top of the building, as long as the distance to the building (100 ft. in this case) is known. Calculate the height of the building.

$$\text{tan}(19.3^{\circ}) = \frac{o}{100}$$
Here I'm calling o the height of the building above our 5 ft. mark. We'll have to add that 5 ft. to the total before we finish. We can rearrange to solve for o, multiplying by 100 ft. on both sides:
$$o = 100 \cdot \text{tan}(19.3^{\circ}) = 35$$
So the height of the building is that 35 ft. plus the 5 ft. height of the instrument, or 40 ft.
Interesting fact: The tangent function is approximately equal to the line $y = x$ between, say, ±π/6. Here are overlapping graphs to show this:
ApproximationGraph.png)
This means that tan(π/6) is approximately π/6. Now π/6 is about 15˚, so for angles of elevation between about ±15˚, we can make a pretty good estimate of the height of objects without even calculating the tangent ... But ... this only works if we use radians instead of degrees. In this problem, the approximation would have yielded a building height of just under 39 ft. Not too bad.
The unit circle — the fundamental basis for trigonometry
Units of Angle Measure
In trigonometry and many subfields of math, we use the unit radians for angle measure. The radian arises more or less naturally from the geometry of the circle. There are 2π (yes, 6.283 ..., but we usually just say 2π) radians in a circle, so 180˚ = π radians. The figure on the left shows the most frequently-used radian measures. They are generally multiples of π/6 (30˚) and π/4 (45˚).
You should memorize this unit circle, including the radian measurements. It will grease the wheels for what's ahead. The tool below might help. It reduces the task to simple counting by multiples of 30˚ and 45˚. If you come back to it once in a while, a little more will sink in each time and soon you'll have it.
Radians and degrees
There are $2 \pi = 6.28$ radians and 360˚ in a circle, $\pi$ radians and 180˚ in a half circle.
Usually, we don't multiply the $\pi$ when reporting radian measurements. We just say 1.1$\pi$ radians, and so forth.
Unit circle learning tool
Press the forward arrow as many times as you want to advance the arrow and find the angle, in degrees and radians, on the unit circle.
The circle is "counted around" in 180˚ increments, then in 90˚, 45˚ and 30˚ increments. Go around the circle enough times that you can correctly anticipate the next angle, both in degrees and radians.
Press the
Pro tip: I can't emphasize enough how important it is that you know your way around the unit circle. Now that that's (hopefully) done, we can take a deeper look at the trigonometric functions.
The special triangles
These two essential right triangles, their angle measures and the ratios of their side lengths will pop up time and again throughout your studies and work in math and science. Knowing how to jot them down and use them, and from where the measurements came, will be invaluable to you. Study them carefully and memorize their proportions.
The 45-45-90 triangle
The 45-45-90 triangle is just what it sounds like, a right triangle that has two 45˚ angles, and is thus an isosceles triangle. We'll work with just symbols for the lengths of the sides, like this:

Now the Pythagorean theorem has to hold for this right triangle, so
$$x^2 + x^2 = r^2$$
Now combine the like terms on the left,
$$2x^2 = r^2$$
and let's solve for $x$ (you'll see why in a minute), by first dividing both sides by 2.
$$x^2 = \frac{r^2}{2}$$
Now to solve for $x$, take the square root of both sides:
$$x = \sqrt{\frac{r^2}{2}}$$
Taking the square root of the numerator gives $r$, with $\sqrt{2}$ in the denominator:
$$x = \frac{r}{\sqrt{2}}$$
Finally, just for completeness, not that it really matters mathematically, the denominator of such an equation is usually "rationalized" by multiplying by $\sqrt{2}/\sqrt{2}:$
$$x = \frac{r \sqrt{2}}{2}$$
Now imagine if we let $r$, the length of the hypotenuse of our triangle, be 1. Then we get this triangle, complete with side measures:
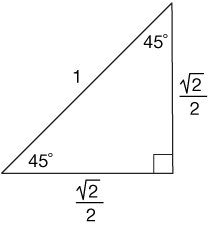
What's great about such a triangle, is that it will give us the lengths of the sides of a 45-45-90 triangle with any hypotenuse length because we have the ratios of the side lengths, $1:\sqrt{2}/2.$
The 30-60-90 triangle
The 30-60-90 (degrees) right triangle is another frequently-encountered triangle that's worth knowing a lot about.

It isn't quite as easy to find an expression for the side lengths $x$ and $y$, unless we combine two of these triangles to form an equilateral triangle like this:

Notice here that I've replaced $x$ from the original figure with $r/2$. We know that the gray vertical line both bisects the top 60˚ angle (by construction) and bisects the base of the triangle. For a proof the the angle bisector of an isosceles triangle also bisects the opposite side, click here.
Now we can set up the Pythagorean theorem for one of the two 30-60-90 triangles shown:
$$r^2 = y^2 + \left( \frac{r}{2} \right)^2$$
Squaring the last term gives
$$r^2 = y^2 + \frac{r^2}{4}$$
Let's solve for y in terms of r by separating terms across the = sign:
$$y^2 = r^2 - \frac{r^2}{4}$$
The difference on the right is easy to calculate; just use 4 as a common denominator:
$$y^2 = \frac{3r^2}{4}$$
Now taking the square root of both sides gives
$$y = r \frac{\sqrt{3}}{2}$$
Now if we take $r = 1$, we arrive at the prototype 30-60-90 triangle:

So for a 30-60-90 triangle, the shorter leg (recall that the sides that form the right angle of a right triangle are called "legs") has a length that is half the length of the hypotenuse, and the longer leg is $\frac{\sqrt{3}}{2}$ of the hypotenuse.
The special triangles.
45-45-90

30-60-90

Trigonometry – trigonometric functions
Now we want to use the unit circle to create the three major trigonometric functions,
- $f(x) = \text{sin}(x)$
- $f(x) = \text{cos}(x)$
- $f(x) = \text{tan}(x)$
We'll do that by drawing a series of triangles, both 45-45-90 and 30-60-90, inside of the unit circle, and calculating the trig function values.
Let's start at 30˚ = θ/6. Notice that we can use that triangle to calculate all three trig functions. We'll set those aside as we work around the circle with triangles, and look at all of the values together at the end of the trip.

Now we really should work our way around the circle in increments of 30˚, but I'm going to skip around a bit and hope you'll get the idea. Next is a 135˚ angle, or 45˚ past 90˚, working counterclockwise (as usual) around the unit circle.
One quirk of the unit circle is that the length of the radius (the hypotenuses of all of our triangles) is always 1, but the other triangle sides can have negative or positive values. That's how certain sine, cosine or tangent values end up negative.

You might have noticed that the 90˚ (which we passed up) angle doesn't really define a triangle. The key to understanding what happens there is to consider an 89˚ angle, in which the opposite side is very small and the adjacent side is nearly equal to the hypotenuse, making the sine function small (close to zero) and the cosine function close to one. Well, at 90˚, those values are zero and one, respectively, and we make similar arguments at all of the multiples of 90˚ around the circle.
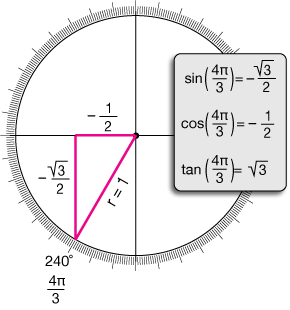
Now let's do a 240˚ = 4θ/3 angle. Notice that because the x-and y-coordinates of the tip of the radius are negative, we treat the sides of our triangle as negative, and that affects the values of the trig functions.
Finally, let's look at an angle in the 4th quadrant, 315˚ = 7θ/4, which is seven increments of 45˚ around the unit circle, and produces a 45-45-90 triangle, just with some "negative" sides.

Notice that all of this would just repeat as we moved our radius vector around the unit circle again and again. Next we'll gather all of this data in a table and determine some patterns in the sine, cosine and tangent functions.
Trig functions are periodic
Here's a table of trig function values at key angles in one round trip of the unit circle.
| $\theta$ (deg.) |
$\theta$ (rad.) |
$\text{sin}(\theta)$ |
$\text{cos}(\theta)$ |
$\text{tan}(\theta)$ |
||
|---|---|---|---|---|---|---|
| $0$ | $0$ | $0$ | $\frac{\sqrt{0}}{2}$ | $1$ | $\frac{\sqrt{4}}{2}$ | $0$ |
| $30^{\circ}$ | $\frac{\pi}{6}$ | $\frac{1}{2}$ | $\frac{\sqrt{1}}{2}$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{3}}{3}$ |
| $45^{\circ}$ | $\frac{\pi}{4}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{2}}{2}$ | $1$ |
| $60^{\circ}$ | $\frac{\pi}{3}$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{3}}{2}$ | $\frac{1}{2}$ | $\frac{\sqrt{1}}{2}$ | $\sqrt{3}$ |
| $90^{\circ}$ | $\frac{\pi}{2}$ | $1$ | $\frac{\sqrt{4}}{2}$ | $0$ | $\frac{\sqrt{0}}{2}$ | $\infty$ |
| $120^{\circ}$ | $\frac{2\pi}{3}$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{3}}{2}$ | $-\frac{1}{2}$ | $-\frac{\sqrt{1}}{2}$ | $-\sqrt{3}$ |
| $135^{\circ}$ | $\frac{3\pi}{4}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{2}}{2}$ | $-\frac{\sqrt{2}}{2}$ | $-\frac{\sqrt{2}}{2}$ | $-1$ |
| $150^{\circ}$ | $\frac{5\pi}{6}$ | $\frac{1}{2}$ | $\frac{\sqrt{1}}{2}$ | $-\frac{\sqrt{3}}{2}$ | $-\frac{\sqrt{3}}{2}$ | $-\frac{\sqrt{3}}{3}$ |
| $180^{\circ}$ | $\pi$ | $0$ | $\frac{\sqrt{0}}{2}$ | $-1$ | $-\frac{\sqrt{4}}{2}$ | $0$ |
The trigonometric functions are repetitive, or cyclic, and we usually refer to them as periodic, meaning that they repeat the same basic pattern predictably.
Forget about the gray columns for now. You can pick up a bunch of patterns as we walk around the circle and look at $\text{sin}(\theta)$, $\text{cos}(\theta)$ and $\text{tan}(\theta)$. Notice that the tangent function is a different beast, and we'll get to that later. Notice also that both the sine and cosine functions oscillate between ±1 and pass periodically through $y = 0$.
The gray columns are just re-expressions of the sine and cosine values to the left. Each is just re-stated with a square root in the numerator so that the increasing-decreasing pattern is more obvious.
The signs of the trig functions change according to which quadrant the tip of radius vector is in (UL = upper left, LR = lower right, and so on). This table shows how the sign of each function depends on the quadrant of the angle:
| Quadrant | sin(θ) | cos(θ) | tan(θ) |
|---|---|---|---|
UR (I) |
+ |
+ |
+ |
UL (II) |
+ |
— |
— |
LL (III) |
— |
— |
+ |
LR (IV) |
— |
+ |
— |
Graphs of the trig functions
Graphs of the sine (black) and cosine (
All of the points in the table above are plotted on this graph. Be sure to think about these graphs for a while.
Notice a few patterns: They oscillate between ±1; they cross or are farthest apart (vertically) at multiples of $\pi/4$ and $\text{sin}(\theta)$ is the same as $\text{cos}(\theta)$, but shifted to the right by $\pi/2$.
These curves are also referred to as "sine waves". We usually don't say "cosine waves" because the cosine function is the same as the sine, just shifted by $\pi/2$. It is common to represent many periodic natural phenomena using sine and cosine curves: Waves, the motion of a pendulum, the motion of a bouncing spring, for example.

Transformations of the trig functions
In order to model periodic behavior using sines and cosines, we need, as usual, some transformations to translate and scale our function at will. In our typical way (see functions section), the transformations of $f(x) = sin(x)$ are shown on the right.
When we use trig. functions to model real data later, we'll make a slight modification of this prototype equation in order to keep the units straight.
The transformations of the other trig. functions are analogous.

Horizontal stretching
Move the slider to change $c$ in the function $f(x) = sin(f/c)$ to get an idea of the effect of horizontal stretching on a periodic function. The function is written both as $f(x) = sin(x/c)$ and as $f(x) = sin[(1/c)·x]$.
If this function represented a wave (e.g. a sound, light or water wave) then the horizontal stretching parameter, $c$, would change the wavelength, the domain distance between successive peaks or troughs. The parameter $f = 1/c$ is called the frequency factor.
Notice that for small c, the frequency (number of cycles on the graph) is large, and for small $c$, it's large. Because the sine function is odd, when $c$ is negative, the sine curve is inverted across the x-axis.
(Notice also that the graph disappears when we try to divide by zero!)
Vertical stretching
Move the slider to see the effect of the vertical-stretching parameter, $A$, on our sine function.
If this function represented a wave like a sound or light wave, the vertical distance between $f(x) = 0$ and the maximum (or minimum) value of the sine function would be the amplitude, which would be proportional to volume (loudness) of sound or brightness (intensity) of light.
Notice that when $A \lt 0$, the function is reflected across the x-axis, as we would expect for any function.
Vertical and horizontal translation
Vertical translation of a periodic function is performed just like on any other function: Simply add a constant number (k) to the value of the function for each point in the domain. Vertical translation is used in modeling to move the average value of the function up or down. For example, to model a tide that fluctuates by ± 3 feet from an average depth of 10 feet, we'd want a sine or cosine function (turns out it doesn't matter which), that oscillates between 7 and 13 feet. The function would read f(some stuff) + 10.
Horizontal translation is very important when we model waves because it represents a property called phase. In our tide example, we might need to shift our model wave over to the right a bit to get the timing of the tides just right (and we'd also have to adjust the wavelength, which would represent the time between high or low tides). Phase is extremely important in many areas of science like x-ray crystallography (used to study molecular structure) and medical imaging.
Reciprocal trig functions: The tangent function
The tangent of an angle (θ) is the ratio of the sine of that angle to its cosine: tan(θ) = sin(θ)/cos(θ). Because cos(θ) can be zero, the graph of the tangent function will have vertical asymptotes, as shown on the right. The tangent of odd multiples of π/2 is infinite because cos(π/2) (and odd multiples of π/2) is zero.
This has an interesting consequence if you are a rock climber or a linesman (person who strings cable, e.g. electric wires, from pole to pole. You'll find an explanation here.
There are three other trigonometric functions left to explore, and like the tangent, all are ratios of other trig. functions, so we can expect asymptotic behavior there, too.

All six trigonometric functions
Finally, let's define the three other trig. functions. The reciprocal of the sine function (not to be confused with the inverse) is called the cosecant (csc) function. The reciprocal of the cosine is (paradoxically, I know) the secant (sec) and the reciprocal of the tangent is the cotangent (cot). csc(θ), sec(θ) and cot(θ) are defined below.

Pro tip: Remembering sec, csc and tan
It should be easier to remember which of the main trig. functions are connected to sec, csc and tan, but due to an accident of history, it's not. Sine should go with secant, and cosine should go with cosecant. Unfortunately, those are reversed, and you'll have to remember that. Tangent goes with cotangent, though!
Graphs of the Trigonometric Functions
Several cycles of each of the six trig functions are plotted below. Note that the sin(x) and cos(x) graphs are vertically expanded by a factor of ten compared to the other graphs. This means that the sine graph would fit in between the U-shaped graphs (they are not parabolas!) in the csc(x) graph, same for the cos(x) and sec(x) graphs. Except for sine and cosine,
all of the trig functions are ratios of other trig functions, thus the vertical asymptotes. Study the figure for a while and note the similarities. These graphs have more in common than they have differences. There is no need to memorize them if you know how they're related and why the have the shapes they have.

There is much more to trigonometry than can fit into one section like this. You'll need to know how to use inverse trig. functions, how to relate trig functions to one another (analytic trig), and how to use trigonometry on non-right triangles. Here are links to other trigonometry-related pages:
Practice problems 2
For problems 1-4, calculate the measure of any missing angles and the lengths of any missing sides of the triangle.
| 1. |
|
| 2. |
|
| 3. |
|
| 4. |
|
| 5. |
A surveyor knows the depth of the canyon and can measure the angle shown. Calculate the distance from one side of the canyon to the other.
|
The small-angle approximation
Here's an interesting problem and an opportunity to show how approximations can be good and save a lot of time. Consider a boat out on the ocean, a distance d from a lighthouse of known height – in this case 25 m. We'll explore two ways of calculating the distance to the lighthouse. Our measurement from the boat is the angle of elevation between the horizontal (sea surface) and the top of the lighthouse, 2˚.

First, let's do this in the straightforward way using the tangent function. First let's convert the angle to radians, because we'll use it that way later:
$$2^{\circ} \left( \frac{\pi \, \text{rad}}{180^{\circ}} \right) = 0.03491 \, \text{rad}$$
The tangent of the angle is
$$tan(0.03491 \, \text{rad}) = \frac{25 \, m}{d},$$
so the distance is
$$d = \frac{25 \, m}{tan(0.03491 \, \text{rad})} = 715.836 \, m$$
Now let's do that in a different way. Notice that the circle of radius d is shown, and that, to a good approximation, the part of that circle that crosses through the lighthouse is almost a line. That is, if we take a small enough part of any curve, it's nearly a line.
If we approximate that the length of the arc is about the length of the lighthouse, and recall that arc length (s) when using radians is
$$s = r \theta,$$
Then we can solve for the radius of the circle (which is the distance, d, here) like this:
$$r = \frac{s}{\theta} = \frac{25 \, m}{0.03491 \, \text{rad}} = 716.127 \, m$$
That's a difference of only about 0.04%, not to bad. When the angles are small, the small-angle approximation is a good one. This may not seem like such a big deal, but it turns out that when we calculate trig. function values on a computer, it takes a lot of time, relatively-speaking. The number of multiplications (or divisions) is the key. Our approximation just takes one division while calculating a tangent value can take several. In a computer program that might execute millions of these calculations, that can be a significant savings – if you can afford the small loss of precision.
Video examples
1. Counting around the unit circle
You should know how to label the most-frequently-used angles around the unit circle (circle of radius r = 1), both in degrees and radians. It's not that difficult if you just think of it as counting around the circle in different increments.
Minutes of your life: 3:25
2. The special triangles: 45-45-90 and 30-60-90
You'll make your journey through trigonometry much easier if you memorize everything needed to derive the trig functions of 30˚, 45˚ and 60˚ angles. Here's how to do it.
Minutes of your life: 3:42
3. Using basic right-triangle trigonometry
Here are two examples of how we use SOH-CAH-TOA trig. to solve for the missing sides of a right triangle. This is a basic skill in trigonometry that you should master.
Minutes of your life: 4:48 (two examples)
mnemonic
A mnemonic (nee·mon'·ick) is a word or phrase designed to help a person remember something. An example would be the pseudo-word "ROYGBIV" or the phrase "Rogers of York Gave Battle in Vain." Both are designed to help us remember the colors of the visible spectrum: red, orange, yellow, green, blue, indigo & violet.
The Greek alphabet
| alpha | Α | α |
| beta | Β | β |
| gamma | Γ | γ |
| delta | Δ | δ |
| epsilon | Ε | ε |
| zeta | Ζ | ζ |
| eta | Η | η |
| theta | Θ | θ |
| iota | Ι | ι |
| kappa | Κ | κ |
| lambda | Λ | λ |
| mu | Μ | μ |
| nu | Ν | ν |
| xi | Ξ | ξ |
| omicron | Ο | ο |
| pi | Π | π |
| rho | Ρ | ρ |
| sigma | Σ | σ |
| tau | Τ | τ |
| upsilon | Υ | υ |
| phi | Φ | φ |
| chi | Χ | χ |
| psi | Ψ | ψ |
| omega | Ω | ω |

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.









