This page is a general introduction to infinite series. Use it to learn the basics and terminology – that's important for moving on. Then use this page to jump to
Arithmetic and geometric series are some of the simplest to understand. You should study them first. Power series and Taylor series are best understood after studying differential calculus. p-series are related to geometric series, and Fourier series are infinite series based on trigonometric functions.
Here's the cool thing about infinite series
$$sin(x) = \frac{x^1}{1!} - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \dots = \sum_{n = 0}^{\infty} \frac{(-1)^n x^{2n + 1}}{(2n + 1)!}$$
$$cos(x) = \frac{x^0}{0!} - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \dots = \sum_{n = 0}^{\infty} \frac{(-1)^n x^{2n}}{(2n)!}$$
$$e^x = \frac{x^0}{0!} + \frac{x^1}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} = \sum_{n = 0}^{\infty} \frac{x^n}{n!}$$
Almost any function can be rewritten as an infinite sum of similar simple terms. In your study of series, you'll learn how to form them, and why they're useful. For example: When you calculate a sine or cosine on your calculator or a computer, the machine doesn't look the value up in a table or draw a unit circle or a right triangle; it does it using a series representation of the function.
For a review of the factorial function, $f(x) = x!,$ look here.
Functions like sine, cosine, the natural exponential function $f(x) = e^x,$ and many others can be expressed as an infinite series of terms of various patterns. In mathematics, a sequence is just a string of numbers, like 1, 2, 3, ... or 3, 6, 9, 12, ... A series is the sum of all the terms of a sequence, like the examples above.
Now these series are, of course, just approximations of sin(x), cos(x) and ex, but the thing is, by adding more terms in the predictable sequence of terms, we can make them as precise as we'd like. In fact, series like these are how your calculator actually calculates sines, cosines and other functions.
A series is a sum
In mathematics, a series is a sum of many (perhaps an infinite) number of terms. The terms of a series generally follow a predictable sequence that can usually be expressed in the shorthand of summation notation.
Summation notation
Before embarking on our discussion of series, we have to get used to (or get reacquainted with) summation notation. We use the capital Greek letter sigma, $\Sigma$, to indicate a sum of terms that have a similar pattern.
To the right of the sigma is a model term (xi in both sums on the right). The variable i is an index or counting variable. We generally use i, j, k, l, m & n to stand for integer counting variables.
Under the $\Sigma,$ we write the starting value of i. It starts at 1 in the upper series and zero in the lower.
Above the $\Sigma,$ we write the final value of i, 10 in the upper series and infinity in the lower; the lower series has an infinite number of terms and the upper series only has 10 terms.
The variable i may be involved in the term model in a variety of ways.
$$f(x) = \sum_{i = 1}^{10} \; x_i$$
The sum of terms indexed by i, beginning with i = 1, and ending with i = 10.
$$f(x) = x_1 + x_2 + x_3 + \dots + x_{10}$$
$$\sum_{i = 0}^{\infty} \; x_i$$
The sum of terms of the form xi indexed by i, beginning with i = 0 and continuing infinitely.
$$f(x) = x_0 + x_1 + x_2 + x_3 + \dots$$
i is a counting variable or index, and changes by +1 for every term: i = 0, 1, 2, 3, ...
Summation notation
Examples of summation notation
Here are some examples of short finite series represented in summation notation. You should make sure you understand how each represents the terms of the series.
$$\sum_{n = 1}^5 \; \frac{(-1)^{2n + 1}}{n} = -\frac{1}{1} - \frac{1}{2} - \frac{1}{3} - \frac{1}{4} - \frac{1}{5}$$
2n + 1 is always odd, so the numerator is always -1
$$\sum_{n = 1}^5 \; \frac{(-1)^n}{n} = -\frac{1}{1} + \frac{1}{2} - \frac{1}{3} + \frac{1}{4} - \frac{1}{5}$$
n alternates between even and odd, so the terms of the series do, too. This is an alternating series.
$$\sum_{n = 0}^4 \; \left( \frac{\pi}{4} \right)^n = 1 + \frac{\pi}{4} + \frac{\pi^2}{16} + \frac{\pi^3}{64} + \frac{\pi^4}{256}$$
$$\sum_{n = 1}^4 \; \frac{n^2}{(2n + 1)!} = 0 + \frac{1}{3!} + \frac{4}{5!} + \frac{9}{7!} + \frac{16}{9!}$$
Remember that the summation notation for a series is not the series itself. It is merely a way of describing the series. In fact, there can be many ways to express any series. For example, the third example here can be written like this:
$$\sum_{n = 1}^4 \; \left( \frac{\pi}{4} \right)^{n - 1}$$
Take a minute to convince yourself that this is true.
Convergence – The story of Zeno and Achilles
One of the key features of any series, especially one that we want to stand in for a function, is the idea of convergence. Does the sum of the series reach some finite limit (converge), or does it continue to grow without bound (diverge)?
Consider the story of Zeno and Achilles: The two have an argument and Achilles tells Zeno he's going to have to kill him – shoot him with an arrow. But Zeno says "Go ahead, you won't kill me!"
Achilles: "But that's ridiculous, I've shot and killed many men with my bow, and I'll kill you, too!"
Zeno: "No, my fine friend, your arrow will never reach me!"
Achilles: "Explain yourself, Sir!"
Zeno explains that when Achilles releases his arrow, they would have to agree that it will take a certain amount of time, let's call it t1, to travel half the distance to its target.
Afterward it will take another, smaller but still finite, time, t2, to travel half of the remaining distance.
It will take a time t3 (smaller still, but measurable!) to travel half of the remaining distance, and so on, infinitely. Now, Zeno argues, if we add an infinite number of finite times, even though some are quite small, we end up with an infinite time - the arrow will never reach me!
Achilles fires his arrow and kills poor Zeno dead as a doorknob. The series, each successive term (a time) half of the previous, converges to exactly the time it would take for an arrow to travel between Achilles and Zeno. Zeno was betting that his series was divergent, but it wasn't.
A brilliant student of mine once noted that Achilles could just aim well behind Zeno and put the arrow through him on its way to the first halfway point.
Some series converge to a finite limit, and some diverge. In this table are the first few terms of one of the series shown above, the one that represents f(x) = ex, with x = 1. This important series converges to the number e, the base of all continuously-growing exponential functions. Notice that successive terms only modify digits further and further to the right of the decimal. That's what convergence means: The series approaches a finite limit as the number of terms grows, and it doesn't grow past that limit. Another way to say that is that the series sum is bounded.
Convergent series are the most important kind. Series are usually used to find an alternate route to the value of a function that's difficult to find directly, so we want convergence to some solution. We usually aren't too concerned with series that diverge.
↑ No matter how many terms are added, the numbers in green will no longer change.
Other examples of convergent series
In the table below, the first five terms of the series representations (above) of sin(45˚), cos(45˚) and e1 = e are calculated, summed and compared to the actual value (from a calculator).
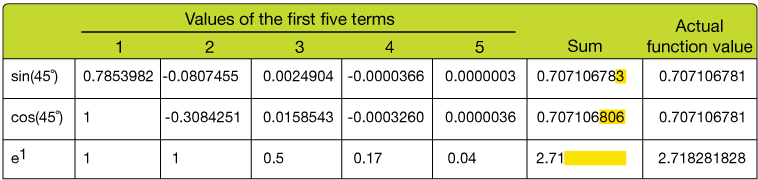
Notice (↑) that after adding just five terms of the series the sine and cosine sums end up very close to the actual values we'd get by using a calculator. The yellow highlights mark the error in the approximation. We say that these series "converge rapidly to the value of the function." The exponential function converges less rapidly — it would take several more terms to reach the precision of our sine and cosine — but it eventually does. You might want to make a similar table on a spreadsheet to show that this is true. (Yeah, I know you won't, but being able to do things like that is a terrifically useful skill).
Your calculator and computers use series approximations like these to calculate sines, cosines, logs and their inverses, and other functions. It's more efficient than storing a table of values, and it makes use of the "native" operations, addition, multiplication, &c.
In your later work in mathematics, you will probably encounter functions that are too cumbersome to work with or even impossible to solve, but that are much easier to use and understand when expressed as a series. Just how we find these series representations is a topic for later. For now just take it for granted that they (usually) exist.
Why mess with series at all?
- Many times when we have to work with certain kinds of functions, the
algebra is too cumbersome and we get nowhere. Re-expressing a function as a series of simpler terms can be very helpful.
- Often we
don't need as much precision as a computer gives us. We can truncate (cut short) the series to give us just the limited precision we need.
- Sometimes the
series representation of a function is much more enlightening at a glance than looking at the function itself. Often it's possible to say something about the shape of the graph in a certain region of its domain more easily by looking at the series.
- Often
finding a derivative or an integral of a function is difficult or impossible, but can be done on the series representation of the function.
Convergence, Boundedness
This graph of the sum of the inverse squares of all of the integers was a challenging problem in mathematics for a long time until it was solved (in 1748) by Swedish mathemetician Leonhard Euler (pronounced Oy'-ler). It's called the Basel problem, named after Euler's home town.
Euler showed that the sum of the series is π2/6, or about 1.645. The graph shows how the sum grows for the first 100 terms of the series. π2/6 is the upper bound of this series, and we say that the series converges to a limit of π2/6.
Just how that limit is found is a subject for another section. For now, you should appreciate that a series converges to a finite limit (or approaches an upper or lower bound) if its terms decrease in size.
Least upper bound, Greatest lower bound
At this point, it might be a little difficult to wrap your brain around the idea of a sum being finite when we're adding an infinite number of terms. It's a paradox and it's completely normal to be confused. Part of that confusion lies in our sloppy terminology. When we say "sum of a series" what we really mean is a least upper bound or a greatest lower bound, a number that the sum approaches but never quite reaches. The sum of a series will never exceed its upper bound, and never be less than its lower bound.
It's just that to the level of precision that we usually need, only a certain number of terms are really needed from any series to get us "close enough" to that boundary. Any additional terms would just further refine the number to higher precision.
If you think about it a bit, the only possible way for a series to have an upper or lower bound — to converge to a finite limit, is if each successive term in the sum gets smaller. We say it this way:
If Σ an converges, then the limit of the size of a term, an, is zero (lim an = 0). Then it must also be true that if lim an = 0, that Σ an diverges.
Here are two simple kinds of series, and you can drill deeper into series at the end of this section.
More examples of convergent/nonconvergent series
Here is a comparison of the growth of two infinite series, the first with terms of the form (½)n and the second with terms 1/n, where n ranges from 1 to 31. Only the growing sum is shown, not the individual terms. The first series converges and the second does not.
Notice that Σ(½)n does not exceed a value of 2.0 as n gets larger. In fact, the sum of the series is 2
$$\sum_{n=1}^{\infty} \, \frac{1}{2^n} = 2$$
But the series on the right doesn't have the same property. It is divergent (doesn't converge). The more terms we add to the series, the larger the sum will grow, even though the size of the terms clearly tends toward zero.
$$\sum_{n=1}^{\infty} \, \frac{1}{n} \; \rightarrow \, \infty$$
If a series is to be used to represent some useful function, we must make sure it's a convergent series, otherwise it won't be of much use.
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.