The sections on thermodynamics ought to be read and worked through in roughly this order:
- Heat (this page) The atomic and molecular nature of heat
- Temperature About measuring temperatures, and temperature scales
- Heat transfer How heat moves from one place to another
- Heat capacity Substances differ in their abilities to absorb heat and reflect it as a temperature rise.
- Thermodynamics The laws of thermodynamics
- Enthalpy Heat content of a system
- Entropy A measure of the disorder of the universe, or a part of it
- Gibbs energy Energy at constant temperature & pressure
What is heat?
You may have heard that there's no such thing as cold. Semantically, that's true. Cold is merely the absence of heat. But what is heat? One thing we know is that when the atoms of one body (an object) are moving more rapidly than those of an identical object, that body is hotter – it contains more heat. Heat is random motion of atoms in a substance. Those atoms may be bound in the molecules of a substance.
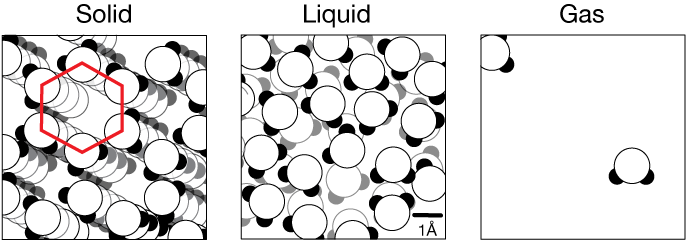
An example: phases of water
Without much of the heat present at room temperature, water exists as the ordered, hydrogen-bonded (see intermolecular forces) crystal ice (left, below).
The random thermal motion of each water molecule is insufficient at temperatures below 0ºC to break four hydrogen bonds (H-bonds) per molecule. As heat is added to ice, the random motion of each water molecule becomes sufficient to break most of the H-bonds (middle panel below). Now H-bonds exist, but they are transient, breaking and reforming frequently. As water absorbs even more heat to become a gas (steam, right panel), each molecule has so much kinetic energy that collisions between molecules increase the spacing between them dramatically, making any lasting contact even more transient.
Heat defined
Heat is random thermal motion, which can occur as translation, rotation and vibration of molecules [or just translation for monatomic substances like argon (Ar)].
A way to think about phases & heat
Imagine that there are 20 of us in a classroom – no desks, and we're holding hands (not necessarily in a big circle, just randomly. The holding of hands will represent hydrogen bonds (or any other weak intermolecular attractions).
If we stay relatively still, perhaps just shuffling our feet a bit, it will be easy to maintain the hand-holding. That represents the situation in a solid. We just don't have enough translational (moving around) or rotational energy to break our bonds.
If we walk around randomly, but calmly, we can probably still hold hands. Sure, once in a while two of us will walk away from each other and lose a grip, but we can quickly reestablish that bond with someone else. So we have some transient bonds, but all-in-all, we're still mostly holding hands. Such is the situation in liquids.
Finally, imagine if we were all running around flat out, bouncing off of walls and moving again. It would be very difficult to hold hands doing that. Grip strength just couldn't overcome the our speeds, and on average, very few bonds would exist for very long. Thats the situation in a gas.
Where heat goes in molecules
Heat is motion — kinetic energy (KE). It's the motion of atoms, molecules, and atoms within molecules. Now we need to tease apart the relationships between the motion of individual atoms in a molecule and the motions of the molecule as a whole.
First, let's make the approximation that the relative positions of atoms in a molecule are fixed - all of the bond lengths and angles remain constant (they don't, but we'll assume that for now). Now there are two ways a molecule can manifest kinetic energy: translation and rotation
Translation
By translation, we mean movement of the whole molecule along any of the three-dimensional coordinates, x, y or z, or any combination thereof. The three Cartesian coordinates form a set of "basis vectors" for translation. Any translation at all can be thought of as a sum of various parts translation along the x, y or z axes. Generally, we identify a unique point in the molecule, the center of mass, and refer to the translation of the center of mass; the rest of it goes along for the ride.
Rotation
A molecule can also rotate about its center of mass. For most molecules, there are three (never more) independent and perpendicular axes of rotation that are analogous to our three Cartesian axes.
For linear molecules, like CO2 (O=C=O) or H2, rotation about the molecule's long axis carries very little kinetic energy because the nuclei are all on the axis of rotation and electrons are very light. Any rotation at all can be expressed as a sum of various parts of rotation around these three principle axes of rotation.
Vibration
Now when we relax the constraint on movement of atoms within molecules, we get vibration. In any molecule, bonds between atoms can stretch, compress and bend, and they always do. In any molecule, we can always identify a number of "normal modes" of vibration (it's 3N-5 modes for linear molecules and 3N-6 modef for non-linear molecules, where N is the number of atoms and the 5 or 6 are the 3 translations and 2 or 3 rotations), or "normal vibrations" that are the analogs to translation along the Cartesian axes. Any vibration of a molecule can be expressed as a sum of various parts of its normal modes.
You should check out the section on water to see animations of its three normal modes of vibration.
These three translations, three rotations and N vibrational motions are called degrees of freedom of movement of the molecule, or just degrees of freedom.
Kinetic energy of a water molecule
Water is a simple, but important example of a molecule. It consists of a central oxygen atom bound to two hydrogen atoms in a bent configuration, as illustrated below. Here are the nine "modes" of expression of kinetic energy – the energy of motion – of the water molecule. A water molecule can translate (atoms can do that, too), rotate and vibrate.
Translation
A water molecule can translate along any of the x-, y- or z-axes of a 3-D Cartesian grid. Any translation, any path at all, can be described by some translation in the x-direcion, some in the y-direction and some in the z-direction.
Rotation
Any rotation of a water molecule can be described as part rotation around the x-axis, as shown below (left), around the y-axis and around the z-axis. In the same way that the three linear axes of the Cartesian coordinate system form a basis for any translation, so do these three rotations form a basis set of simple rotations.
Vibration
Finally, the atoms bonded together in the water molecules can stretch and bend those bonds. It's beyond the scope of this text to describe, but we can find three vibrational normal modes of vibration that will likewise form the basis for any vibration of water whatsoever. These vibrations are called ν1, ν2 and ν3, the symmetric bend, the symmetric stretch and the asymmetric stretch, respectively.
Equipartition of energy
Now we know that any molecule has three "boxes" in which to "store" kinetic energy: translation, rotation and vibration. Notice that a larger molecule (more atoms) obviously has more places to store KE because it has more kinds of vibration or more "vibrational degrees of freedom." Every (nonlinear) molecule has three degrees of translational freedom, three degrees of rotational freedom and 3N-6 degrees of vibrational freedom. A linear molecule has 3N-5 degrees of vibrational freedom.
For most substances over a broad range of temperatures, the law of equipartition of energy holds. It says that energy tends to be distributed evenly over all of the degrees of freedom of a molecule. This has consequences for substances with more and fewer atoms. In the diagram below, each container represents a degree of freedom. The situations for a 3-atom and a 10-atom molecule are illustrated.
The Zeroth Law of Thermodynamics
There are three laws of thermodynamics (1st, 2nd, 3rd) that we will learn in subsequent sections, but often the zeroth law is cited because it lays a good foundation for what comes.
The 0th law says that heat always flows from a hotter object to a cooler one, and never the other way.
This is our general experience with things, though we might need a slight paradigm shift to see it.
When ice is added to a drink, for example, the ice doesn't add cold to the drink. Instead, the ice soaks up heat from the warmer liquid, making it cold.
When you touch a cold surface (by which we mean a surface that contains less heat than your hand), heat flows from your hand to the surface. It's always like this: Heat flows from the warmer object to the hotter object until the two are the same temperature, and the heat lost by the hotter object is equal to the heat gained by the cooler object and the surroundings. When you touch a cold object, it feels cold because the heat from your hand is transferring to the cold object. That transfer of heat away from you is what you experience as cold.
paradigm
A paradigm (pair' - a - dime) is a way of seeing something. For example, one way of seeing school is that it is only about accumulating good grades. Another (a paradigm shift for some) is that it is about learning as much as possible about the world.
0th law of thermodynamics
Heat always flows from an object that contains more heat to an object that contains less, and never the other way.
Notation, units and sign convention
We generally use the letter q (or Q) to denote heat; I will generally use the lower case in these web pages.
By long-standing convention, when a system adds heat to its surroundings (loses heat in an exothermic process), the heat is negative (q < 0). When heat is added to a system (endothermic process), the heat is positive (q > 0). Think of this sign convention as being focused on the system; what does the system do?
If it gives off heat, q is negative. If it takes in heat, q is positive.
The SI unit of heat is the Joule (J). 1 J = 1 Kg·m·s-2. Often, in the United States, we still use the calorie. 1 cal = 4.184 J, and 1 cal is the amount of heat required to raise the temperature of 1 cm3 (or 1 ml) of pure water from 0˚C to 1˚C. And remember that we use two kinds of calories, "large C" and "small c." A large-C calorie is one kcal, or 1000 small-c calories.
Heat: Sign convention
You can think of a system as being "self-centered." It's all about the world from the point of view of the system
If q > 0, (+q) heat was added to the system in a process (endothermic)
If q < 0, (-q) heat was removed from the system and added to the surroundings by the system (endothermic)
Heat: Units
The unit of heat in the SI system is the Joule:
$$1 \, J = 1 \, \frac{Kg \, m^2}{s^2}$$
Another common unit of heat is the calorie. In common use, we often refer to "large C" and "small C" calories, C and c. A large-C calorie is also referred to as a Kcal (Kilocalorie).
$$1000 \, c = 1 \, Kcal = 1 \, C$$
Finally, $1 \, c = 4.184 \, J.$
Nutritional calories
The common nutritional calorie, like the 140 calories in a can of Coke®, are actually large-C calories (Kcal), so 140 nutritional or food calories means 140,000 cal (small-c).
Equivalence of heat and work
Doing work on a system or adding heat to it are completely equivalent. The total energy input into a system is the heat it receives plus the work done on it; it's part of the principle of conservation of energy.
Prescott Joule, one of the early developers of thermodynamics, performed an experiment that showed that mechanical work done on a container of water produces a temperature rise in the water equivalent to the amount of heat needed to cause the temperature change.
In Joule's experiment, weights of known mass were dropped a known distance, thus producing a known amount of kinetic energy that produced mechanical stirring of a quantity of water. A temperature rise roughly equivalent to that amount of energy as heat was then observed in the water.
It's important to remember as you move through thermodynamics that heat and mechanical work are equivalent, just as work, potential energy and kinetic energy can be interchanged in mechanical systems.
As you begin to study state functions, you'll begin with the internal energy change of a system, which is the sum of the changes in heat and work.
Practice problems
| 1. | The average apple contains about 95 food Calories (95,000 cal) of energy. How much energy is this in Joules?
|
| 2. | A liter of gasoline contains about 3.15 MJ of energy. Convert this to Kcal.
|
| 3. | The British Thermal Unit (BTU) is still used in industry. 1 BTU = 1.055 × 103 J. A typical heating and cooling unit for a 2000 sq. ft. home in the U.S. has a heating (or cooling) capacity of around 90,000 BTU. How many Joules is 90,000 BTU?
|
Cartesian coordinates
Cartesian coordinates are the normal 2-dimensional (2D) or 3-dimensional (3D) coordinate systems we most-frequently use. In two dimensions, we draw x- and y-axes at 90˚ angles to each other, and in 3D we add a third axis, usually the z-axis, perpendicular to the x-y plane.
The location or direction of an point or particle can be described using Cartesian coordinates (x, y) in the 2D plane, or (x, y, z) in 3D.
SI units
SI stands for Système international (of units). In 1960, the SI system of units was published as a guide to the preferred units to use for a variety of quantities. Here are some common SI units
| length | meter | (m) |
| mass | Kilogram | (Kg) |
| time | second | (s) |
| force | Newton | (N) |
| energy | Joule | (J) |
semantic
Semantic is an adjective meaning related to the precise meaning (of a word) in language. Sometimes arguments over substantive things get mired in semantics, other times, it's the precise meaning of a word or words that really matter. We need to be mindful about the real intent of an argument.
Translation
Translation is motion in one or more of the three Cartesian (x, y, z) directions, or a combination of them, without any rotation.
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2014, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.