Representing functions using sin(x) & cos(x)
We very often need to construct series representations of functions; usually there is some big advantage in doing so. We'd like those series to converge to the value of the function using as few terms as possible. A good place to start is with a series with terms resembling the parent function. As a very simple example, consider representing the sin(x) and cos(x) functions near x = 0 using a linear model.
Recall that a linear approximation of a curve at some point is really just the equation of the line tangent to that curve at that point. A linear approximation of the cosine function at x = 0, for example, has the same value and slope as cos(x) at x = 0.
Here are the calculations for finding those linear approximations:
| f(x) | f(0) | f' | f'(0) | point |
|---|---|---|---|---|
| sin(x) | 0 | cos(x) | 1 | (0, 0) |
| cos(x) | 1 | -sin(x) | 0 | (0, 1) |
The resulting linear approximations are
$$ \begin{align} sin(x): \; \rightarrow \; y = x \\[5pt] cos(x): \; \rightarrow \; y = 1 \end{align}$$
Now let's take a look at the sine approximation more closely. Here is a table of sines of 0, 0.01, 0.1 and π/4, using both the approximation and a precise value from a calculator.
| $x$ | $\approx sin(x)$ | $sin(x)$ | $\Delta$ |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0.01 | 0.01 | 0.01 | 0 |
| 0.1 | 0.1 | 0.099 | 0.001 |
| $\pi/4$ | 0.785 | 0.707 | 0.078 |
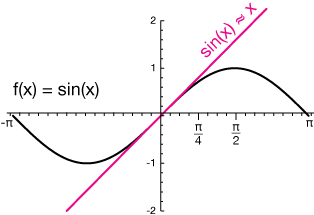
Here is a plot of sin(x) and y = x near x = 0. Notice that the sine function is approximately linear between -π/2 < x < π/2. It's actually a very good approximation, when asked what the sine of 0.01 is, to reply, "about 0.01." You can see that even at x = π/4, the approximation is good to within about 10%.
Now let's look at the cosine approximation. Near x = 0, the cosine function is quite curved. Take a look at the graph of cos(x) and its approximation.

The table below gives values of cos(x) and its approximation for x = 0, 0.01, 0.1 and π/4. The error in cos(π/4) is about 40%, much worse than the linear sin(x) approximation at x = 0.
| $x$ | $\approx cos(x)$ | $cos(x)$ | $\Delta$ |
|---|---|---|---|
| 0 | 1 | 1 | 0 |
| 0.01 | 1 | 0.999 | 0.001 |
| 0.1 | 1 | 0.995 | 0.005 |
| $\pi/4$ | 1 | 0.707 | 0.293 |
A better model of the cosine function in the region around x = 0 might be something like a parabola, such as $f(x) = -x^2 + 1.$ At least that function curves downward like the cosine curve does.
Fourier series are infinite series composed of periodic functions (sine and cosine), so they're well-suited for modeling other periodic functions.
The type of functions on which an infinite series are called basis functions. The basis functions of Taylor and MacLaurin series are polynomial functions. The basis functions of Fourier series are sine and cosine functions.
It is usually best to model a function using a series with basis functions similar to the original function.
![]()
This section might require some background review. These sections might be helpful:
The Fourier series
The Fourier series (named for its originator, French mathematician Joseph Fourier (1768-1830) — I don't know where we'd be if not for French mathematicians), is a series composed of trigonometric basis functions sin(x) and cos(x). The Fourier series representing a periodic function with a period of 2L is:
$$f(x) = a_o + \sum_{n = 1}^{\infty} a_n cos \left( \frac{n\pi x}{L} \right) + \sum_{n = 1}^{\infty} b_n sin \left( \frac{n\pi x}{L} \right)$$
where the $a_n$ and $b_n$ are adjustable coefficients allowing us to "mix" a certain amount of sine and cosine in every term, and m and n are integers. Notice that if we want to use a Fourier series to represent the a sine function with a period of $L$ raised or lowered by $a_o$ units, all of the $b_n$ coefficients are zero and we only need one term for complete convergence.
Finding $a_n$ and $b_n$ – orthogonality
When we found our coefficients of the Taylor series, we insisted that the value and all of its derivatives of our function and its series representation be the same at some central point. For the Fourier series, we use a different method of finding those coefficients, relying on the orthogonality of the basis functions sin(x) and cos(x).
When two functions are orthogonal, then when we multiply them and integrate over a symmetric interval, often $-\infty \; \text{to} \; \infty,$ the result is zero.
Finding the coefficients of the Fourier series involves three equations:
$$ \begin{align} \int_{-L}^L cos \left( \frac{m\pi x}{L} \right) cos \left( \frac{n\pi x}{L} \right) \, dx &= L \delta_{mn} \\[5pt] \int_{-L}^L cos \left( \frac{m\pi x}{L} \right) sin \left( \frac{n\pi x}{L} \right) \, dx &= 0 \\[5pt] \int_{-L}^L sin \left( \frac{m\pi x}{L} \right) sin \left( \frac{n\pi x}{L} \right) \, dx &= L \delta_{mn} \end{align}$$
where $\delta_{mn}$ is called the Kronecker delta, and is defined like this:
$$ \delta_{mn} = \left\{ \begin{array}{ll} 1 & if \; m = n \\[3pt] 0 & if \; m \ne n \end{array} \right. $$
Preparations
We'll do these integrals below, but first we need to review some useful trig. identities. First the power-reduction formulae for sine and cosine:
$$ \begin{align} sin^2(x) &= \frac{1 - cos(2x)}{2} \\[5pt] cos^2(x) &= \frac{1 + cos(2x)}{2} \end{align}$$
Next, some sine·cosine product identities:
$$ \begin{align} sin(a) sin(b) &= \frac{1}{2}[cos(a - b) - cos(a + b)]\\[5pt] cos(a) cos(b) &= \frac{1}{2}[cos(a - b) + cos(a + b)]\\[5pt] sin(a) cos(b) &= \frac{1}{2}[sin(a - b) + sin(a + b)] \end{align}$$
Now we'll do each of the orthogonalization integrals, making use of those identities and the properties of even and odd functions, namely:
$$ \begin{align} &\int_{-a}^a f_{odd}(x) \, dx = 0 \\[5pt] &\int_{-a}^a f_{even}(x) \, dx = 2 \int_0^a f_{even} \, dx \\[5pt] &\int_{-a}^a f_{odd} \cdot f_{even} \, dx = 2 \int_0^a f_{odd} \cdot f_{even} \, dx \end{align}$$
The last equation is because the product of an even and an odd function is an even function. Recall that for an even function, $f(-x) = f(x),$ and for an odd function, $f(-x) = -f(x).$
Orthogonalization integrals
I'll leave these hidden to simplify the page. Click for the details of each integral. It's a good exercise to look at the first, then try to do the second on your own.
$\int_{-L}^L sin\left( \frac{n\pi x}{L} \right) sin \left( \frac{m\pi x}{L} \right) \, dx = \delta_{mn}$
Show the integral steps
We'll this integral in two cases, $m = n = 0,$ and two cases together: $m = n \ne 0,$ and $m \ne n.$
n = m = 0: In this case, because sin(0) = 0, the sine part of the integrand is zero, so the integral is zero.
n = m ≠ 0
n ≠ m
$$ \begin{align} &\int_{-L}^L sin \left( \frac{n\pi x}{L} \right) cos\left( \frac{m\pi x}{L} \right) \, dx \\[5pt] &= \frac{1}{2} \int_{-L}^L sin \left( \frac{(n - m) \pi x}{L} \right) + sin \left( \frac{(n + m)\pi x}{L} \right) \, dx &= -\left[ \frac{L}{(n - m)\pi} cos\left( \frac{(n - m)\pi x}{L} \right) + \frac{L}{(n + m)\pi} cos\left( \frac{(n + m)\pi x}{L} \right) \right]_{-L}^L \\[5pt] &= 0 \; \text{ for all n = m, n ≠ m} \end{align}$$
The conclusion that this integral is zero is because it's an integral of an even function over a symmetric interval. So we have:
$$\int_{-L}^L sin \left( \frac{n\pi x}{L} \right) cos\left( \frac{m\pi x}{L} \right) \, dx = 0$$
$\int_{-L}^L cos\left( \frac{n\pi x}{L} \right) cos \left( \frac{m\pi x}{L} \right) \, dx = \delta_{mn}$
Show the integral steps
We'll consider this integral in three cases, $m = n = 0,$ $m = n \ne 0,$ and $m \ne n.$
n = m = 0: In this case, because cos(0) = 1, the integrand is 1, so the integral is $x\bigg|_{-L}^L = L - (-L) = 2L.$
n = m ≠ 0
$$ \begin{align} \int_{-L}^L cos^2 &\left( \frac{n\pi x}{L} \right) \, dx \\[5pt] &= \frac{1}{2}\int_{-L}^L 1 + cos\left( \frac{2n\pi x}{L} \right) \, dx \\[5pt] &= \frac{1}{2} \left[ x + \frac{L}{2n\pi} sin\left( \frac{2n\pi x}{L} \right)\right]_{-L}^L \\[5pt] &= \frac{1}{2}[L -(-L)] = L \end{align}$$
n ≠ m
$$ \begin{align} &\int_{-L}^L cos \left( \frac{n\pi x}{L} \right) cos\left( \frac{m\pi x}{L} \right) \, dx \\[5pt] &= \frac{1}{2} (2)\int_0^L cos\left( \frac{(n - m)\pi x}{L} \right) + cos\left( \frac{(n + m)\pi x}{L} \right) \, dx \\[5pt] &= \frac{1}{2} \left[ \frac{L}{(n - m)\pi} sin\left( \frac{(n - m)\pi x}{L} \right) + \frac{L}{(n + m)\pi} sin\left( \frac{(n + m)\pi x}{L} \right) \right]_0^L \\[5pt] &= \frac{L}{(n - m)\pi} sin[(n - m)\pi] + \frac{L}{(n + m)\pi} - 0 + 0 \\[5pt] & = 0 \end{align}$$
Because n and m are integers, then n±m are integers, and sin(kπ) = 0 for integer k, the sine terms vanish, so the integral = 0. So our result is
$$\int_{-L}^L cos \left( \frac{n\pi x}{L} \right) cos\left( \frac{m\pi x}{L} \right) \, dx = L \delta_{mn}$$
Here we're ignoring the trivial case where n = m = 0, which will be un-interesting for our Fourier series.
$\int_{-L}^L sin\left( \frac{n\pi x}{L} \right) cos \left( \frac{m\pi x}{L} \right) \, dx = 0$
Show the integral steps
We'll this integral in two cases, $m = n = 0,$ and two cases together: $m = n \ne 0,$ and $m \ne n.$
n = m = 0: In this case, because sin(0) = 0, the sine part of the integrand is zero, so the integral is zero.
n ≠ m
$$ \begin{align} &\int_{-L}^L sin \left( \frac{n\pi x}{L} \right) cos\left( \frac{m\pi x}{L} \right) \, dx \\[5pt] &= \frac{1}{2} \int_{-L}^L sin \left( \frac{(n - m) \pi x}{L} \right) + sin \left( \frac{(n + m)\pi x}{L} \right) \, dx \\[5pt] &= -\left[ \frac{L}{(n - m)\pi} cos\left( \frac{(n - m)\pi x}{L} \right) + \frac{L}{(n + m)\pi} cos\left( \frac{(n + m)\pi x}{L} \right) \right]_{-L}^L \\[5pt] &= 0 \; \text{ for all n = m, n ≠ m} \end{align}$$
The conclusion that this integral is zero is because it's an integral of an even function over a symmetric interval. So we have:
$$\int_{-L}^L sin \left( \frac{n\pi x}{L} \right) cos\left( \frac{m\pi x}{L} \right) \, dx = 0$$
Calculating $a_0, \; a_n \; \text{ and } \; b_n$
Now we are in position to find the coefficients ao, am and bm using our orthogonality relationships. To find am, we begin with our definition of the Fourier series for a function:
$$f(x) \approx a_o + \sum_{n = 1}^{\infty} a_n cos\left( \frac{m\pi x}{L} \right) + \sum_{n = 1}^{\infty} b_n sin\left( \frac{n\pi x}{L} \right)$$
Now multiply both sides of that equation by $cos\left( \frac{n\pi x}{L} \right)$ and integrate from -L to L:
$$\int_{-L}^L f(x) cos \left( \frac{n\pi x}{L} \right) \, dx = \int_{-L}^L a_o \, dx + \int_{-L}^L \sum_{n = 1}^{\infty} a_n cos \left( \frac{m\pi x}{L} \right) cos \left( \frac{n\pi x}{L} \right) \, dx + \int_{-L}^L \sum_{n = 1}^{\infty} b_n sin \left( \frac{n\pi x}{L} \right) cos\left( \frac{n\pi x}{L} \right) \, dx$$
Now we can do a little trick here to get rid of the ao term. Notice that cos(0) = 1, so we can incorporate that term into our first sum, like this:
$$\int_{-L}^L f(x) cos \left( \frac{n\pi x}{L} \right) \, dx = \int_{-L}^L \sum_{ \color{#E90F89}{n = 0}}^{\infty} a_n cos\left( \frac{m\pi x}{L} \right) cos \left( \frac{n\pi x}{L}\right) \, dx + \int_{-L}^L \sum_{n = 1}^{\infty} b_n sin\left( \frac{n\pi x}{L} \right) cos \left( \frac{n\pi x}{L}\right) \, dx$$
A couple of things about this expression. First, we're using one of the important properties of integrals, that the integral of a sum is a sum of integrals. Now on the right side, the integral with a sine and a cosine part is zero by our orthogonality formulas above. Likewise, the integral with two cosines is equal to L when m = n. So we have
$$\int_{-L}^L f(x) cos\left( \frac{m\pi x}{L} \right) \, dx = a_m L.$$
Now look at the cos·cos integral again and substitute n = 0, then we have
$$\int_{-L}^L cos(0) cos(0) \, dx = \int_{-L}^L \, dx = L - (-L) = 2L.$$
So we now have both of our a constants,
$$ \begin{align} a_o &= \frac{1}{2L} \int_{-L}^L f(x) \, dx \\[5pt] a_n &= \frac{1}{L} \int_{-L}^L f(x) cos\left( \frac{n\pi x}{L} \right) \, dx \end{align}$$
To find the bn coefficients, we again begin with the definition of the Fourier series, just multiplying by $sin\left( \frac{n\pi x}{L} \right)$ this time.
Show bn calculation steps
$$f(x) \approx a_o + \sum_{n = 1}^{\infty} a_n cos\left( \frac{m\pi x}{L} \right) + \sum_{n = 1}^{\infty} b_n sin\left( \frac{n\pi x}{L} \right)$$
Multiply by $sin\left( \frac{n\pi x}{L} \right)$
$$\int_{-L}^L f(x) sin \left( \frac{n\pi x}{L} \right) \, dx = \int_{-L}^L \sum_{ \color{#E90F89}{n = 0}}^{\infty} a_n cos\left( \frac{m\pi x}{L} \right) sin \left( \frac{n\pi x}{L} \right) \, dx + \int_{-L}^L \sum_{n = 1}^{\infty} b_n sin \left( \frac{n\pi x}{L} \right) sin \left( \frac{n\pi x}{L} \right) \, dx$$
Now the sin·sin integral is L as long as m = n, and the mixed sin,cos integral vanishes by our orthogonality relationships, so we end up with
$$b_n = \frac{1}{L} \int_{-L}^L f(x) sin \left( \frac{n\pi x}{L} \right) \, dx$$
Fourier coefficients
The Fourier coefficients, $a_0, \; a_n \; \text{ and } \; b_n$ are:
$$ \begin{align} a_o &= \frac{1}{2L} \int_{-L}^L f(x) \, dx \\[5pt] a_n &= \frac{1}{L} \int_{-L}^L f(x) cos\left( \frac{n\pi x}{L} \right) \, dx \\[5pt] b_n &= \frac{1}{L} \int_{-L}^L f(x) sin \left( \frac{n\pi x}{L} \right) \, dx \end{align}$$
Using Fourier series
Now lets do a few examples of how we use Fourier series to represent other periodic functions.
Example 1
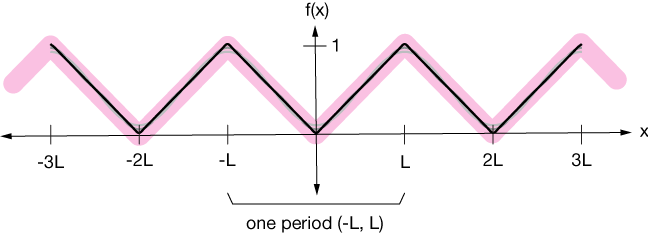
Find a Fourier-series representation of the sawtooth function, shown below. The central segment is y = x (-L < x < L), the second is y = x - 2L (L < x < 3L), and so on.
Among a few other uses, the sawtooth wave is commonly used in music synthesis to produce unique sounds. The dashed vertical parts aren't really there; the function is discontinuous, but they help us visualize the wave, and you'll see that our Fourier series will incorporate them into a continuous function.

Our Fourier series representation will look like
$$f(x) = a_o + \sum_{n = 1}^{\infty} a_n cos \left( \frac{n\pi x}{L} \right) + \sum_{n = 1}^{\infty} b_n sin \left( \frac{n\pi x}{L} \right)$$
But we can do a little better. First, notice that the sawtooth wave is a purely odd function [f(-x) = -f(x)]. That means we can drop the (even) cosine terms from the Fourier definition for this function.
$$f(x) = a_o + \sum_{n = 1}^{\infty} b_n sin \left( \frac{n\pi x}{L} \right)$$
Now the a0 coefficient is found using
$$a_o = \frac{1}{2L} \int_{-L}^L f(x) \, dx = \frac{1}{2L} \int_{-L}^L x \, dx$$
But that integral vanishes because it's the integral of an odd function (f(x) = x) over an even interval, so a0 = 0. Now we're just left calculating the bn coefficients:
$$b_n = \frac{1}{L} \int_{-L}^L f(x) \cdot sin \left( \frac{n\pi x}{L} \right) \, dx$$
Incorporating f(x) = x and focusing on the interval (-L, L), the bn are
$$b_n = \frac{1}{L} \int_{-L}^L x\cdot sin \left( \frac{n\pi x}{L} \right) \, dx = \frac{2}{L} \int_{0}^L x\cdot sin \left( \frac{n\pi x}{L} \right) \, dx$$
In the second step above, we've recognized that the integrand is the product of two odd functions, so it's even, and we can split the interval in half, integrating from 0 to L, and just multiply by 2. It's always convenient to have a zero limit of integration.
To do the integral, first do a simplifying substitution:
$$\frac{2}{L} \left( \frac{L}{n\pi}\right)^2 \int_0^{n\pi} a \cdot sin(a) \, da$$
With all of the coefficients out of the way and the limits converted to "a-space" limts, this integral can be done by parts. It is:
$$ \begin{matrix} \text{Let } \; u = a && dv = sin(a) \, da \\[5pt] \text{then } \; du = da && v = -cos(a) \end{matrix}$$
$$ \begin{align} \int_0^{n\pi} a \cdot sin(a) \, da &= -a\cdot cos(a) + \int cos(a) \, da \\[5pt] &= -a \cdot cos(a) + sin(a)\bigg|_0^{n\pi} \\[5pt] &= -n\pi \cdot cos(n\pi) + sin(n\pi) - 0 - 0 \\[5pt] &= -n\pi \cdot (-1)^n \end{align}$$
Putting our constants back in and finishing the integral gives
$$\frac{2}{L} \left( \frac{L}{n\pi}\right)^2 \int_0^{n\pi} a \cdot sin(a) \, da = \frac{-2L(-1)^n}{n\pi}$$
Our sawtooth wave approximation is a series of sine terms:
$$f(x) \approx \sum_{n = 1}^{\infty} \frac{-2L(-1)^n}{n\pi} \, sin\left( \frac{n\pi x}{L} \right)$$
Here is a plot of some of our approximations superimposed upon the sawtooth target. The black curve is the first five terms, the magenta curve is the sum of the first twenty. The gray curves are sums of 10 and 15 terms.

A couple of comments on this series representation of the sawtooth wave.
Example 2
Calculate a Fourier series representation of the square-wave function below, in which
$$ \delta_{mn} = \left\{ \begin{array}{ll} 1 & if \; 0 \le x \lt L \\[3pt] 0 & if \; -L \le x \lt 0 \end{array} \right. $$
and $f(x + 2L) = f(x)$

Our Fourier series representation will look like
$$f(x) = a_o + \sum_{n = 1}^{\infty} a_n cos \left( \frac{n\pi x}{L} \right) + \sum_{n = 1}^{\infty} b_n sin \left( \frac{n\pi x}{L} \right)$$
Now the way this function is situated on our axes makes it purely odd, so we can do without the cosine term and write our initial model as
$$f(x) = a_o + \sum_{n = 1}^{\infty} b_n sin \left( \frac{n\pi x}{L} \right)$$
Now the a0 coefficient is found using our formula for ao, but notice that we have to break up the integral of this piecewise function:
$$ \begin{align} a_o &= \frac{1}{2L} \int_{-L}^L f(x) \, dx \\[5pt] &= \frac{1}{2L} \int_{-L}^0 \, 0 \, dx + \frac{1}{2L} \int_{0}^L \, 1 \, dx = L - (-L) \\[5pt] &= \frac{1}{2L}(L - 0) = \frac{1}{2} \end{align}$$
Now all that's left is to find the bn coefficients, remembering to split the integral accordingly:
$$ \begin{align} b_n &= \frac{1}{L} \int_{-L}^L f(x) \, sin \left( \frac{n\pi x}{L} \right) \, dx \\[5pt] &= \frac{1}{L}\int_{-L}^0 \, 0 \, sin \left( \frac{n\pi x}{L} \right) \, dx + \frac{1}{L}\int_{-L}^0 \, 1 \, sin \left( \frac{n\pi x}{L} \right) \, dx \\[5pt] &= \frac{-1}{n\pi} cos\left( \frac{n\pi x}{L} \right) \bigg|_0^L \\[5pt] &= \frac{-1}{n\pi} [cos(n\pi) - cos(0)] \\[5pt] &= \left\{ \begin{array}{ll} 0 & \text{if n is even} \\[3pt] \frac{2}{n\pi} & \text{if n is odd} \end{array} \right. \end{align}$$
Now we need to write out some terms of our series so we can figure out a simple way to write the repeating term. The basic series is
$$ \begin{align} f(x) &\approx a_0 + b_1 cos(x) + b_2 cos(2x) + b_3 cos(3x) + \dots \\[5pt] &= \frac{1}{2} + \frac{2}{\pi} sin(x) + \frac{2}{3\pi} sin(3x) + \frac{2}{5\pi} sin(5x) + \dots \end{align}$$
In the last equation above, all of the even terms zero out. Now odd integers can be written as (2n ± 1), where n is a integer. The 2 ensures that 2n is even, and adding one ensures that the resulting number is odd. It's a common trick with infinite series. We'll use 2k - 1 for convenience:
$$f(x) \approx \frac{1}{2} + \sum_{k = 1}^{\infty} \frac{2}{(2k - 1)\pi} sin[(2k -1)x].$$
The graph below shows our square wave with two of our series sums superimposed, one with k = 5, the other (black) with k = 20 terms.


Here are three series sums, with n = 5, 10 and 20, bottom to top. Notice that as we add terms, the side "walls" get straighter and the wiggles get smaller. A particular feature of Fourier series representations – like the sawtooth wave above or this square wave – is the little blip at sharp corners. Still, the Fourier series representation of even functions like these can be very valuable in doing other kinds of calculations.
Method recap
To recap what we did in this somewhat lengthy problem
- Write the general form of the Fourier series and consider the symmetry of the target wave. This might allow deletion of odd or even terms.
- Solve for the remaining coefficients (ao, an and/or bn) by using the orthogonalization integrals, keeping in mind any symmetry tricks,
- Put the series together and try to identify a simple common term, again using the symmetry and zero properties of the trig functions, such as $sin(n\pi) = 0.$
Important caveats about Fourier series
There are a couple of important aspects of Fourier series that we've glossed over here, but they should be noted and addressed.
- We haven't shown that the Fourier series form a complete set. A complete set of functions is capable of representing any other function, if enough terms are combined in the correct proportions. For Fourier series, that means high-enough n, and the proper coefficients, ao, an and bn. The set of sine and cosine functions is, in fact, a complete set, but we won't prove that here.
- The other thing we haven't considered is the convergence of each of our series. In general, Fourier series representing periodic functions that have limits on their range are convergent, but that wasn't proved here.
Practice problems
| 1. |
Find the Fourier series representation of the triangle wave shown below. The period of the function is $2L,$ and $f(x) = f(x + 2L).$ For $-L \lt x \lt L,$ $f(x) = |x|.$
|
|
| 2. |
Determine the Fourier coefficients of the wave form represented by $f(x) = sin\left( 8\pi x + \frac{\pi}{4} \right).$ |
|
| 3. |
Determine the Fourier coefficients of the wave form in the figure below, and write a simple expression for the terms of its Fourier series.
|
Converge
A function converges to a certain number if its value approaches that number ever more closely, but never actually reaches it. An example is the function f(x) = 1/x2, which converges to a value of zero as x → ∞.
Likewise, an infinite series converges if the sum of its terms has a limit – an asymptote – that it approaches but never crosses.

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2016, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.